一种泵车臂架模态分析中液压油缸的等效方法
2013-03-31钟志宏吴运新
钟志宏,吴运新
(1.中南大学机电工程学院,湖南长沙410083; 2.中南大学高性能复杂制造国家重点实验室,湖南长沙410083)
混凝土泵车是一种用于混凝土浇注的大型工程机械,主要由底盘、混凝土泵和臂架系统组成[1]。其中,臂架系统是最能反映混凝土泵车设备特点的部件,其安全性、可靠性和先进性是决定泵车核心竞争力的关键,结构如图1所示。
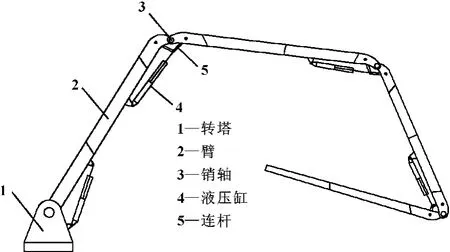
图1 泵车臂架结构简图
实际工作时,臂架姿态可以连续变化,其整体刚度和质量分布也相应变化,进而导致其应力分布及动态特性的变化[2]。因此,了解泵车典型工况下的应力状态及动态特性如固有频率和振型,对于泵车的安全使用与维护具有重要的意义。
根据模态理论,在不考虑阻尼影响的情况下,模态主要由系统刚度和质量决定。对于臂架模态分析,通常用二力杆 (Rod)来模拟液压油缸[1-4],然而其等效刚度如何确定却鲜有文献论及。同时,在进行臂架多姿态模态分析时,液压油缸长度变化但质量基本保持不变,这就要求杆单元的密度也要相应变化以保持质量不变。作者将讨论臂架模态分析时液压油缸等效刚度与等效密度的确定方法,然后依此方法对某臂架模型典型工况进行了模态分析,最后进行了试验验证。
1 液压油缸的等效模型
1.1 等效刚度
1.1.1 液压油的刚度
在一般液压系统中,液压油都被当作刚性不可压缩的。这是由于液压油压缩量较小,其影响在轻载和慢动作系统中微不足道,常常忽略不计。然而在泵车臂架系统中,液压油微小的压缩量会在臂架末端产生非常显著的位移,而液压油的刚度又远小于钢材的刚度,所以液压油缸的刚度在臂架整体刚度中起着至关重要的作用,从而在限元建模过程中需要准确计算其等效刚度。
在液压系统中,液压油实际上以弹簧的方式压缩,其刚度k可以表示为:

式中:p为压强;A为压缩面积;h为压缩位移。
液压油的体积弹性模量E定义为在压强为p时,原始体积V与被压缩体积量ΔV之比,即:

可推出:

式中:l为油液长度;其他同式(1)。
把式(3)代入式(1),可得液压油的刚度:

由式 (4)可以看出,液压油具有和固体材料相同的拉压刚度公式。
1.1.2 液压油缸的等效刚度模型
当臂架位于某一姿态时,平衡阀锁死,因此在计算液压缸的等效刚度时除了考虑缸内的液压油之外,还要考虑液压缸和平衡阀之间的油管内的液压油的刚度[5],如图2所示。
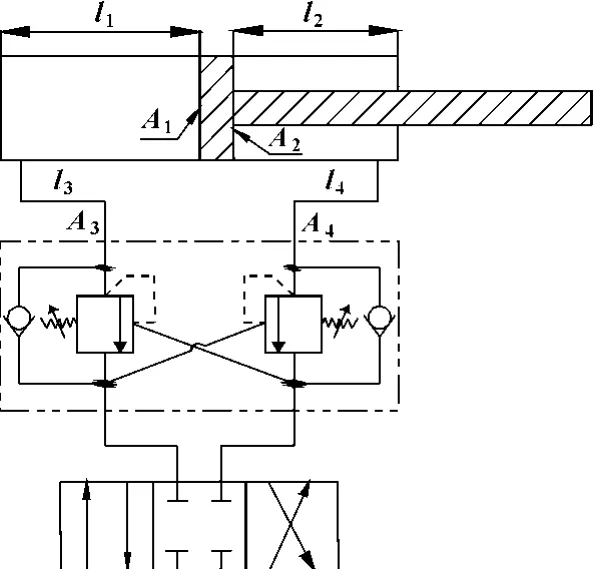
图2 液压油缸系统原理图
根据式 (3),当油压为p时,液压缸无杆腔端液压油本身的压缩位移:

油管内液压油压缩位移:

从而可知由于油管内液压油压缩而引起的缸内油液位移:

根据式(1)可以计算有杆腔端(带油管)的液压油的等效刚度:

把式(5)—(7)代入(8),得

类似的,可知无杆腔端 (带油管)液压油的等效刚度:

图2所示整个液压缸系统可以等效为如图3所示的弹簧质量系统。
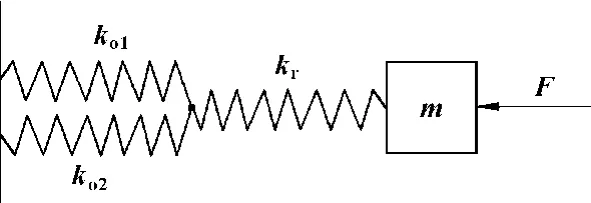
图3 液压油缸等效刚度模型
图3中ko1、ko2分别为液压油缸有杆腔端和无杆腔端液压油的等效刚度;kr为活塞杆的刚度,亦符合式(4)。
根据弹簧联接理论,图3所示系统的等效刚度为:

综上,臂架在任意姿态时可按上述方法计算液压油缸的等效刚度。
1.2 等效密度
臂架姿态变化时,液压缸长度变化但质量不变,在用杆单元等效时可以通过调节杆单元的材料密度ρeq来实现:

式中:m为液压油缸总质量;A为杆单元截面积;l为某姿态下液压缸(杆单元)长度。
2 典型工况模态算例
臂架工作时姿态多变。姿态不同,臂架整体的质量和刚度分布也会发生变化,因此其固有频率及振型也不相同。作者仅选取某臂架地基和面墙两种典型姿态运用MSC.Patran/Nastran进行模态分析,两种姿态下每节臂与水平方向的夹角分别为 [75°,15°,-15°,-75°]、[75°,45°,0°,-45°]。
对比分析结果,发现两种姿态下臂架振型类似,但固有频率有明显差异。因篇幅关系,文中只列出地基工况下臂架前六阶模态振型,如图4所示。其中,第一、四、五阶振型为臂架侧向摆振;第二、三、六阶为臂架自身平面 (x-y平面)内的振动。两种姿态下臂架前六阶固有频率见表1。

图4 地基工况下臂架前六阶振型

表1 臂架前六阶固有频率 Hz
3 试验验证
3.1 试验方案
通过实验模态分析获取臂架系统振型和固有频率的方法复杂,故常用负阶跃激振后测量臂架自由振动时域曲线,然后进行频谱分析获取系统一阶固有频率的方法[6-7]。因为臂架固有频率较低 (低于1 Hz),如果采用加速度传感器则需要传感器具有良好的低频精度,否则将影响试验精度,而这种传感器价格较高。因此,从精度和经济方面考虑,试验采用应变测量。
操作臂架分别运动至上述两种典型姿态,然后在竖直方向拖拽第四节臂末端使臂架发生自身平面内的振动,松开后开始记录臂架自由振动的时域曲线。对时域曲线进行FFT变换获取臂架幅频谱,从而可知对应姿态下臂架自身平面内振动的一阶固有频率(对应模态分析中二阶固有频率)。
3.2 数据处理与分析
3.2.1 地基姿态
地基姿态臂架振动时域曲线及对应频域曲线分别如图5、图6所示。由图6可以看出,臂架地基姿态自身平面内振动的一阶固有频率为0.829 Hz,而对应有限元模态分析所得固有频率为0.877 27 Hz,从而可以计算出仿真分析对于试验数据的相对误差为5.82%。

图5 地基姿态时域曲线
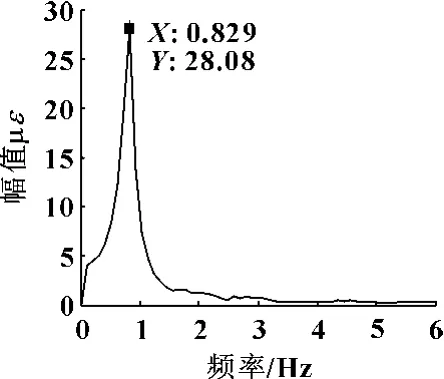
图6 地基姿态幅频谱
3.2.2 面墙姿态
面墙姿态臂架振动时域曲线及对应频域曲线分别如图7、图8所示。由图8可以看出,臂架面墙姿态自身平面内振动的一阶固有频率为0.780 7 Hz,而对应有限元模态分析所得固有频率为0.814 52 Hz,从而可以计算出仿真分析对于试验数据的相对误差为4.33%。

图7 面墙姿态时域曲线

图8 面墙姿态幅频谱
4 结论
首先建立了泵车臂架多姿态模态分析时液压油缸的等效模型,推导了其刚度与密度计算公式,然后对臂架的两种典型姿态即地基与面墙进行了模态分析,最后对两种姿态下的臂架进行了固有频率试验。通过有限元分析结果与试验结果对比发现,仿真分析结果与试验数据误差小于6%,从而验证了文中提出的液压油缸等效模型的准确性。
【1】史先信,郑永生,徐怀玉,等.基于ANSYS的大型泵车臂架有限元分析[J].建筑机械,2009(4):79-82.
【2】吴运新,钟志宏,滑广军.基于MSC.Patran/Nastran的泵车臂架分析系统的研究[J].郑州大学学报:工学版,2010,31(6):83-86.
【3】张艳伟,佟力,孙国正.基于ANSYS的混凝土泵车臂架结构分析研究[J].武汉理工大学学报:交通科学与工程版,2004,28(4):536-539.
【4】宋建安,董忠红,吕彭民.水泥混凝土输送泵车整机模态[J].长安大学学报:自然科学版,2004,24(5):104-106.
【5】戴云飞.液压缸液压刚度的计算[J].有色金属设计,1999,26(1):61-63.
【6】吕彭民,汪红兵,张大庆.混凝土泵车结构模态分析与试验[J].长安大学学报:自然科学版,2004,24(6):74-76.
【7】王海英.水泥混凝土泵车振动性能与结构优化设计研究[D].西安:长安大学工程机械学院,2003.
