BP神经网络分步赋初值算法的研究
2013-03-29池凯莉董林玺
池凯莉,董林玺
(杭州电子科技大学电子信息工程学院,浙江杭州310018)
0 引言
工程中遇到的问题多数是非线性关系,很难用数学模型来计算,而神经网络具有高度非线性映射的性能特点,只要构建合适的网络,就可以以任意的精度逼近任何的非线性映射,所以神经网络有着十分广泛的应用前景,在网络监测以及交通、医疗、农业等方面获得了广泛的应用。该算法的思想是通过梯度下降法修正各层神经元之间的权值,使误差不断下降以达到期望误差的目的。从本质上说,这种算法是一种迭代过程,迭代算法一般都与初值的选择密切相关,如果初值选择不当,则算法的收敛速度会很慢甚至不收敛,在训练过程中也容易陷入局部极小值。研究者一直致力于算法的改进[1],目前已有很多BP网络改进算法产生,如:批处理、增加动量项、变学习效率等,然而,这些改进方法都是基于随机初始化权值进行训练仿真的,所以不能解决对初始权值的依赖问题。
本研究将采用分步赋值的方法设置初始权值。输入到最后一级隐层的权值矩阵对网络的影响不是很大,只要保证网络的抗干扰性和容错性,使网络处于一个很好的状态即可,本研究采用敏感区赋值,通过矩阵相乘来计算各级的权值。最后一层的输出权值直接作用于输出,对算法的影响最大,笔者进行单独赋值,利用期望值作为实际输出构成线性方程组,以方程组的解作为输出层的权矩阵的初始值,这样不仅可以避免陷入局部最小点,同时也可大大地缩短训练的时间。
1 BP神经网络
传统BP神经网络的思想是:学习过程由信号的正向传播与误差的反向传播两个过程组成[2]。正向传播是将样本经过逐层处理后传向输出层,误差反传是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,该信号即作为修正各单元权值的依据。信号正传后误差信号反传,周而复始地进行,该过程就是网络的学习训练过程。该过程一直进行到网络输出的误差减少到可以接受的程度,或进行到预先设定的学习次数为止。
笔者以3层的神经网络为例来阐述神经网络的工作原理[3],其结构图如图1所示。
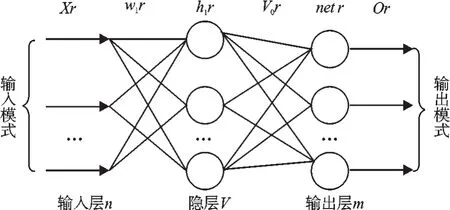
图13 层BP神经网络结构
网络参数如下:输入样本数为k,输入层节点数为n,隐层节点数为v,隐层加权和向量为net,输出层节点数是m,输入层到隐层的权值矩阵为Wij,输出层权值矩阵是Vjk,教师向量是tk,学习效率为η,动量项为ε,输入和隐层之间的激励函数是f1,输出层的激励函数是函数f2,通常激活函数取单极性S变换函数。
2.1 正向传播
定义网络输出和期望输出不等时,输出误差E可以表示为:

第1隐层加权和netj如下所示:

第1隐层输出hj如下所示:

第2隐层的加权和与输出层的输出计算方法同上。
2.2 反向传播
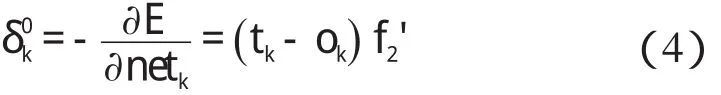
输出层的权值Δvjk变化如下:

隐层的权值Δwij变化表示为:

2 BP神经网络赋初值算法
传统BP神经网络算法采用的反向迭代逐步调整各层权值,最终得到最优权值矩阵,研究者利用该矩阵对样本进行训练校准,得到更准确的信号数据。但是这种标准的BP算法在应用中暴露了不少内在的缺陷。网络是在权初值基础上展开训练的,因此权值的初值是网络训练的最根本的影响因素,有些文献提出了新的赋初值算法[3-4],主要过程如下。
输入和隐层之间的激励函数是线性分段函数f1,输出层的激励函数采用的是sigmoid函数f2。其中:p=1,2,3…k。输入层和隐层、隐层和输出层的权值矩阵分别是:
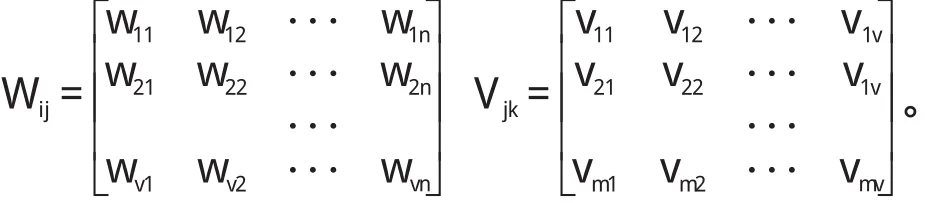
输入层与输出层的隐层分别采用不同的赋初值方法来赋值,方法如下:首先对输入层到隐层的权值赋初值,前层对输出的影响很小,主要考虑的是网络的抗干扰性,使网络处于一个良好的状态,该赋值方法已经被验证是切实可行的。
为了使前层稳定,最后网络收敛到设定精度,本研究选择的激励函数是已经研究很成熟的单极性的S函数,如下所示:
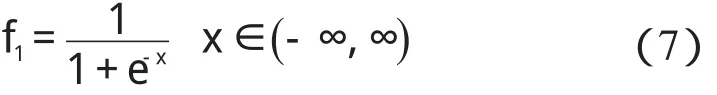
该函数保证隐层的输出和样本保持一致的相关性。其赋值原理可总结如下:
f1的反函数如下所示:
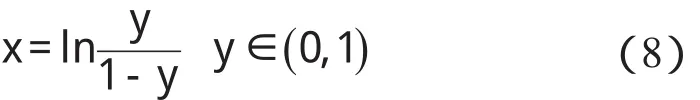
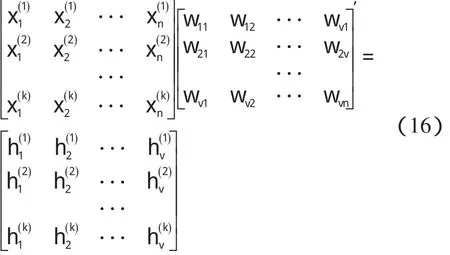
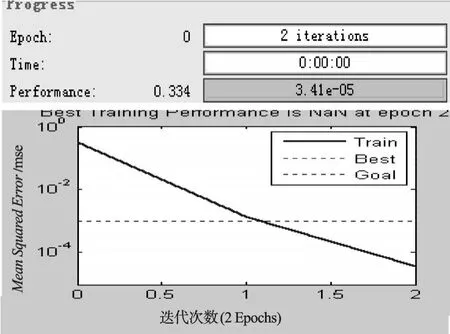
某隐层节点的输出值是a(-1 一个隐节点的输出值为a的等值超平面定义为等值超平面Pa,隐层节点的起始节点为P0,具体计算公式如下: 式中:hw—隐层节点权向量w的单位向量,称为隐层节点方向。 一个隐层节点的a水平敏感区域Aa被本研究定义为节点输出在(0,a)范围内输入区域,敏感区域宽度是由隐层节点的权值和阀值来决定的,从公式(2,3)可以得到a水平敏感区域的宽度Ga可表示为: 本研究采集多组数据,取数据集中的点作为特殊样本输入,该样本是:X=(x1x2x3…xq),其中,q≫n。本研究随机选取两个不同的样本点(xh1xh2)作为输入,如果该两样本点对应的输出相同则重新选择样本点。其中前层隐层的赋初值方法可总结如下: (1)激励函数的敏感区如下: (2)设隐层节点输出为a(-1 (3)隐层的第i个节点(i (4)重复以上3步选择不同的样本值,求出n对权值,这样就可以求出隐层权值矩阵Wij的初值,Wij=(w1w2…wn)T。 如果不只一个隐层,后面的隐层和输出的权值矩阵求解可以表示为: 针对后层隐层权值矩阵这样计算,使得后层的权值矩阵小于前层,保证了网络的抗干扰性。 这种方法虽然在一定程度上避免了局部极小的问题,但是采集样本难度大,并且没有考虑到输出层的独特性和重要性。输出层权值矩阵直接作用于实际输出,直接决定网络训练结果的好坏,所以本研究在前层的赋值基础上,提出了新的赋初值算法,对输出层进行单独的全新赋值。 第1层的权值赋值使用的特殊样本,由最能反映对象规律的数据组成,紧接其后的采集到的数据应该与前面的数据出入不大,此时对后面的权值赋值和前面的赋值连续,是可行的[5]。在此本研究对输出层采用新的方法进行求解,为使输出的数值在一定的范围内,采集k组样本Xp=(x1px2px3p…xnp),其中,p 本研究使用的f2也是单极性的S函数,使输出限制在(0,1)之内,求解线性方程。 其输出层权值矩阵的赋值步骤可总结如下: (1)求取隐层的输出hi,激励函数为f1=x(-1 利用输出期望值tk,求解f2的反函数得到netq,可以表示为: (2)隐层加权和为netq,求取输出层第q节点的权值矩阵Vjk,如下所示: 该方程在vk时有解,为了使网络结果简单,本研究取v=k方程有唯一解。同时第一隐层采取上述方法赋值的理由是: (1)第一层隐层的矩阵赋值方法可以提高网络的抗干扰性。在求解输出层权值矩阵时,前层隐层的输出h矩阵必须是满秩,才能保证公式(16)有解。由于第一层权值举证已经固定,不再变化,本研究多次选择样本输入求解,就可以得到公式(16)的解。 (2)重复上述赋值步骤(1)、(2),输出层剩下的节点对应的权值也可以得到,解得m个k阶方程组即可。通过线性方程组的解和前面得到的输入到隐层的初值就得到了整个网络的权值矩阵。 方程的解是输出层的权矩阵初值,在初值基础上,通过输入样本对网络进行训练就可以得到最优的权值矩阵。本研究利用期望输出来得到初值,十分接近最优权值,通过输入新的样本训练,不仅降低了训练的时间,也解决了局部极小的问题[6-7]。 本研究采用上述方法对神经网络进行赋值,输出层需要求解线性方程组即A X=b,输入大量不同样本来求解,然而通常情况下系数矩阵A是不可逆矩阵,所以就不存在根,得不到相应的输出层的权值矩阵。本研究采用一种Gause-Jardon消元法来解方程组[8],将这个方法解得的输出层权值矩阵和前层的权值矩阵结合在一起,通过仿真验证可知其大大地提高了训练后续样本的速度,是可行的。以下就简要地叙述这种消元法的原理。 线性系统A X=b在生产实践和科学研究中会经常遇到,该矩阵方程的解分为两种情况:当系数矩阵A的行数大于或者等于列数的时候,方程有解,当行数小于列数的时候,方程无解。 当方程无解的时候,即方阵A没有可逆矩阵的时候,一般研究者可以在Frobenius范数意义下,找到一时本研究还要借助广义矩阵[9],来求解此时的逆矩阵。利用广义矩阵求解的矩阵方程A X=b的极小范数最小二乘解的表达式可所示为: 本研究依据的定理是: 按照该方法就可以求出线性方程A X=b的系数矩阵A的广义矩阵,继而可以得到要求的极小范数的最小二乘解。 该实验构建的是3层2-4-1的神经网络,训练算法函数选择是传统的梯度最降法,隐层和输出层的激励函数是单极性S函数,如公式(7)所示。训练次数设为30 000,学习效率为0.05,误差精度为0.001。本研究用传感器采集温度数据,选择样本集中的点利用敏感区赋值,计算出前层的隐层权值。笔者分别利用两种不同算法的赋初值的方式,对后续采集的温度数据进行验证。 采用文献[3]中的赋初值算法得到的仿真结果如图2所示。 图2 赋初值算法仿真图 笔者利用本研究提出的分步赋初值算法训练网络,得到的仿真图如图3所示。 图3 分步赋初值算法仿真图 图2中显示的是BP赋初值算法的误差曲线和训练过程,其误差曲线平滑缓慢的下降,在训练了75次误差接近设定精度的时候,曲线几乎不再变化,整个训练过程历时13 s,平均迭代次数123次。 图3中显示的是采用分步赋初值算法训练的结果,误差训练曲线是直线,误差一直呈直线下降,整个训练小于1 s,迭代2次。 由上述的分析结果可以看出,优化赋初值算法不仅大大地提高了训练的速度,而且使误差函数的下降趋势变得陡峭,在一定程度上避免了陷入局部极小的现象。 本研究分别利用传统的BP神经网络算法和优化的分步赋值算法对样本进行训练,可以看出,优化赋值方法使训练时间缩短到1 s之内,这样就大大地缩短了数据的处理时间,提高了收敛速度;同时训练过程没有出现振荡,误差几乎呈直线下降,克服了传统BP算法的收敛易陷入局部极小的问题。 计算机仿真结果表明该算法是有效的。 ( ): [1]李良,吴红娉,陈瑜.基于BP神经网络算法及推导的研究[J].中国水运,2008,8(1):161-162. [2]韩力群.人工神经网络教程[M].北京:北京邮电大学出版社,2006. [3]侯媛彬.提高神经网络收敛速度的一种赋初值算法研究[J].模式识别与人工智能,2001,14(4):385-389. [4]宋绍云,仲涛.BP人工神经网络的新型算法[J].电脑知识与技术,2009,5(5):1197-1198. [5]陈桦,程云艳.BP神经网络算法的改进及在Matlab中的实现[J].陕西科技大学学报,2004,22(4):44-47. [6]MENG J E.Face recognition with radial basics function(rbf)neural network[J].IEEE Transactions on Neural Networks,2003,3(3):697-710. [7]张潜,武强.基于BP神经网络的一种传感器温度补偿方法[J].电子设计工程,2011,19(9):152-154. [8]SYEDA M,ZHANG Y,PAN Y.Parallel Granular Neural Network forFast Credit Card Fraud Detection[C]//Proceedings of the 2002 IEEE Internatinal Conference on Fuzzy Systerm.2002:572-577. [9]张大志.用Gause-Jardon消去法求解线性方程AX=b的极小范数最小二乘解[J].阜阳师范学院学报,2007,24(3):21-23.



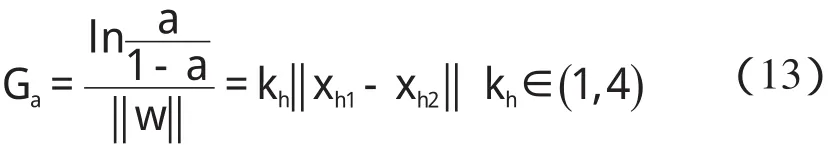


3 BP神经网络新算法

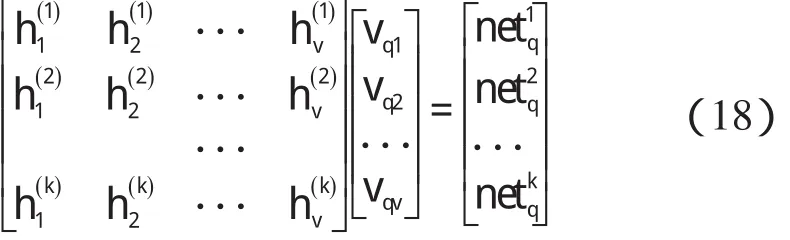


4 Matlab仿真分析与结果

5 结束语
