一类四阶差分方程的混合边值问题

石海平

(广东建设职业技术学院基础部,广东广州 510450)

0 引言

记N,Z及R分别表示自然数集、整数集和实数集.任取a,b∈Z满足a≤b,定义Z(a)=狖a,a+1,…狚,Z(a,b)=狖a,a+1,…,b狚.k为某个正整数.*表示向量的转置.Δ是向前差分算子.

考虑四阶非线性差分方程

及边值条件

其中pn是Z上的正实值函数,f∈C(Z×R3,R).

近年来,作为描述众多实际问题的数学模型,差分方程已广泛出现在科学研究的各个领域中,如概率论、矩阵论、电路分析、组合分析、排队论、数论、心理学与社会学等[1].

方程(1)可看作如下微分方程的离散情形:

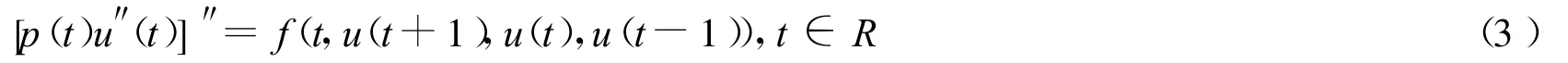
与上述方程(3)相似的方程曾经在研究格动力系统孤立波的存在性中出现过.例如,Smets和Willem[2]研究了类似方程(3)孤立波的存在性.当pn≡1,房辉和赵大鹏[3]以及陈鹏和唐先华[4]分别研究了方程(1)的特殊形式非平凡同宿轨的存在性.

四阶微分方程的边值问题在弹性力学和工程物理中有着广泛的应用[5].李东、方海文及方秀男等[6]研究了四阶微分方程边值问题的正解.在工程实践中,梁的变形计算常常是通过对相应的四阶梁方程的差分格式运用计算机迭代的方法进行的.为了避免迭代的盲目性,在迭代之前对相应差分方程解的存在性的研究则显得十分重要.有鉴于此,本文将应用临界点理论给出一类四阶差分方程混合边值问题解的存在性和多重性的充分条件.研究的主要结果如下.

定理1 对任意的n∈Z(1,k),假设下列条件成立:

(F1)存在泛函F∈C1(Z×R2,R)且F(0,◦)=0,满足

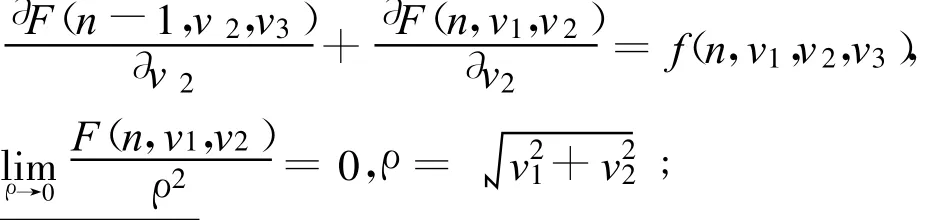
(F2)存在常数β＞2,使得

则边值问题(1)～(2)至少存在两个非平凡解.

注1 (F2)蕴涵存在常数α1＞0,α2＞0,使得

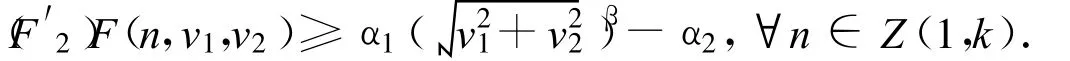
1 变分框架及基本引理

为了应用临界点理论,将引进适当的变分框架及给出一些证明结论所需的引理.首先,介绍一些基本概念.

当k＞2时,对任意的u∈Rk,考虑定义在Rk上的泛函J

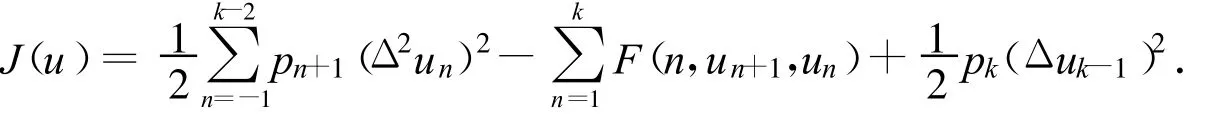
由微积分基本知识及简单的计算,J的Fréchet导数为

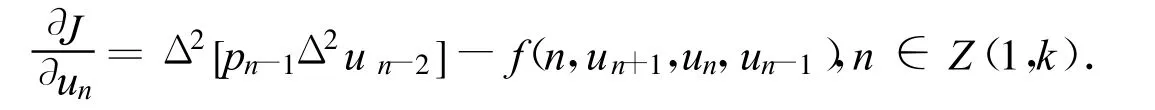
因此,u是J在Rk的临界点,即J′(u)=0当且仅当满足u0,…,uk+2)*是边值问题(1)～(2)的解.因此,寻求边值问题(1)～(2)解的存在性等价于寻求在Rk上泛函J临界点的存在性.

注2 当k=1和k=2时,结论显然成立.为简便起见,省略其证明过程.

定义Rk上的范数为,定义Rk上的另一种范数为‖u‖r=.则存在常数c1,c2,使得c2＞c1＞0,且c1‖u‖≤‖u‖r≤c2‖u‖.

记

由矩阵理论知,D是正定矩阵.设它的特征值为λj＞0,j=1,2,…,k.不妨设

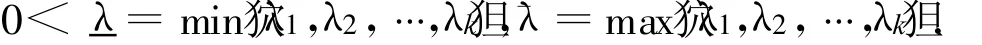
设E是实的Banach空间,J∈C1(E,R),即J是定义在E上的连续Fréchet可微的泛函.称泛函J满足Palais-Smale条件(简称P.S.条件),如果对任意的序列狖u(l)狚⊂E,若狖J(u(l))狚有界且J′(u(l))→0(l→∞),则狖u(l)狚在E中存在收敛的子列.

记Bρ表示在E上中心在原点半径为ρ的开球,∂Bρ表示Bρ的边界.记

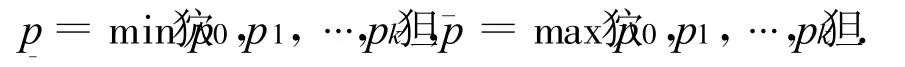
引理1(山路引理[7]) 设E是实Banach空间,且J∈C1(E,R)在E上满足P.S.条件,J(0)=0,且

(J1)存在常数ρ,α＞0,使得

(J2)存在e∈EBρ使得J(e)≤0.

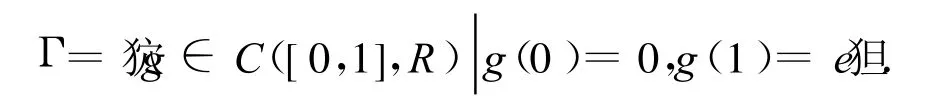
引理2 若条件(F1)及(F2)成立,则J(u)在Rk上满足P.S.条件.

证明 设u(l)∈Rk,l∈Z(1)且狖J(u(l))狚有界.则存在常数M1＞0,使得对任意的l∈Z(1),有-M1≤J(u(l))≤M1.由(F′2),有

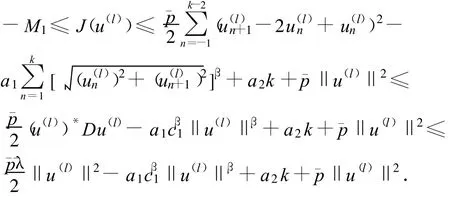
因此

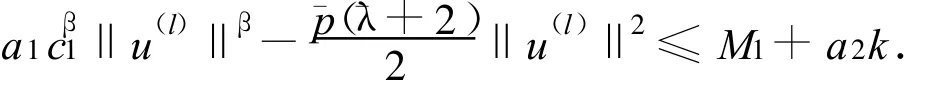
由β＞2知,存在M1＞0,使得对任意的l∈N,有‖u(l)‖≤M1.因此,狖u(l)狚在Rk上有界.从而存在Rk中的收敛子列,即P.S.条件成立.证毕.

2 主要结论的证明

定理1 的证明 由假设易知,J(0)=0.由引理2知,J满足P.S.条件.由(F1),对存在δ＞0,使得当时,有设

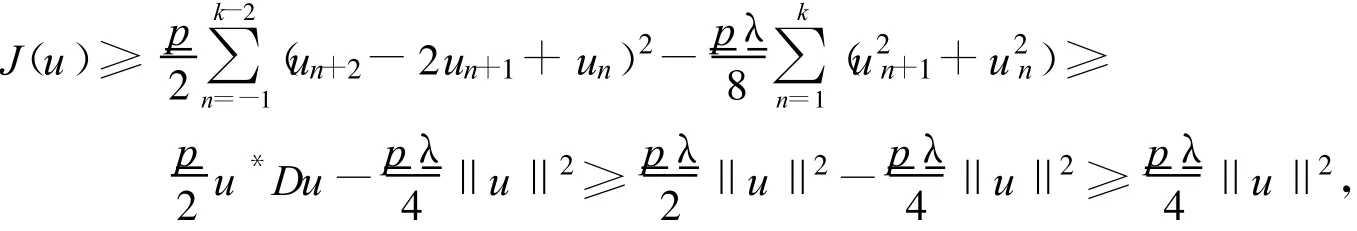
为了利用山路引理,下面验证条件(J2).由P.S.条件的证明过程,知

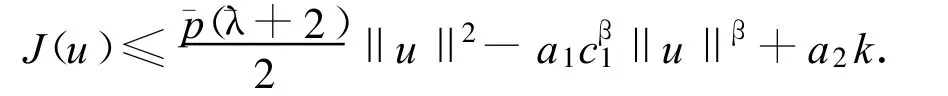
注3 最后,给出一个例子来应用所得的结论.

对任意的n∈Z(1,k),假设

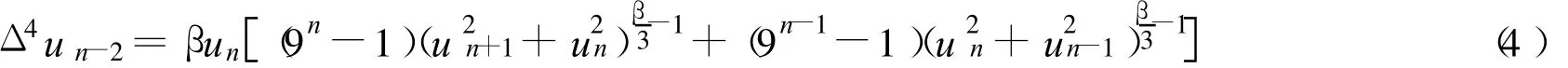
及边值条件(2),其中β＞2.易证,定理1的所有条件成立,故边值问题(2)及问题(4)至少存在两个非平凡解.

[1] Agarwal R P.Difference equations and inequalities:Theory,methods and applications[M].New York:Marcel Dekker,1992.

[2] Smets D,Willem M.Solitary waveswith prescribed speed on infinite lattices[J].J Funct Anal,1997,149(1):266-275.

[3] Fang H,Zhao D P.Existence of nontrivial homoclinic orbits for fourth-order difference equations[J].Comput MathAppl,2009,214(1):163-170.

[4] Chen P,Tang X H.Existence of many homoclinic orbits for fourth-order difference systems containing both advance and retardation[J].Comput Math Appl,2011,217(9):4408-4415.

[5] 唐荣荣.一类伴有边界摄动的非线性奇摄动四阶微分方程三点边值问题[J].应用数学学报,2008,31(2):231-238.

[6] 李东,方海文,方秀男,等.一类带有两个参数变号四阶多点边值问题的正解[J].淮阴师范学院学报:自然科学版,2012,11(6):122-128.

[7] Rabinowitz P H.Minimax Methods in Critical Point Theory with Applications to Differential Equations[M].New York:Amer Math Soc Providence,RI,1986.