具有球对称性的三维热传导方程解的相关性质

钱镜伊, 李同兴

(南京财经大学 应用数学学院, 江苏 南京 210046)

具有球对称性的三维热传导方程解的相关性质

钱镜伊, 李同兴

(南京财经大学 应用数学学院, 江苏 南京 210046)

对于具有球对称性的三维热传导方程进行求解,并分析证明解的唯一性、稳定性、渐进性, 最后给出相应方程的傅里叶变换求解方法.

唯一性; 稳定性; 渐进性; 傅里叶变换

0 引言

当物体内的温度分布只依赖于一个空间坐标,而且温度分布不随时间而变时,热量只沿温度降低的一个方向传递,这称为一维定态热传导.此时的热传导可用下式描述:

式中q为热量通量;T为温度;x为热传递方向的坐标;λ为热导率.此式表明q正比于温度梯度dT,但热流方向与温度梯度方向相反.此规律由法国物理学家傅里叶于1822年首先发现的热传导公式,故称为傅里叶定律.

本文对于具有球对称性的三维热传导方程进行研究,由于受解波动方程求平均法[1]的启发,利用球平均法进行降维,从而可以解出其古典解,并分析解的相关性质.

1 预备知识

1.1 分离变量法

分离变量法是将一个偏微分方程分解为两个或多个只含一个变量的常微分方程,即将方程中含有各个变量的项分离开来,从而将原方程拆分成多个更简单的只含一个自变量的常微分方程.运用线性叠加原理,将非齐次方程拆分成多个齐次的或易于求解的方程.利用高数知识、级数求解知识,以及其他巧妙的方法,求出各个方程的通解,最后将这些通解“组装起来”.

1.2 极值原理[1]

设u(x,t)在矩形RT{α≤x≤β,0≤t≤T}上连续,并且在矩形上连续,并且在矩形内部满足热传导方程(1),则它在矩形的两个侧边(x=α,及x=β,0≤t≤T)及底边(t=0,α≤x≤β)上取得最大值和最小值.换言之,如果以 表示 的两侧边及底边所组成的边界曲线(统称为抛物边界),那么成立着

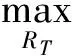
1.3 傅里叶变换[1]

设f(x)是定义在(-∞,∞)上的函数,它在[-l,l]上有一阶连续导数,有

就有

称g(λ)为f(x)的傅里叶变换,记为F(f);称f(x)为g(λ)的傅里叶逆变换,记为F-1(g).当f(x)在(-∞,∞)上连续可导且绝对可积时,它的傅里叶变换存在,且其逆变换等于f(x).

2 主要结论与证明

定理1 对形如下列方程组

(*)

的初边值问题(1)～(4)的形式解为

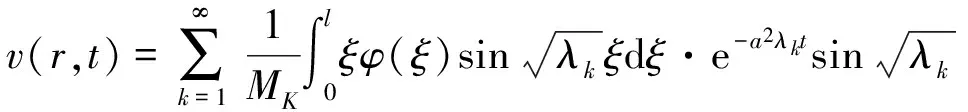
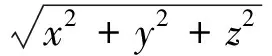
再对上述方程组进行v=ru变换,

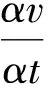
(1)

t=o:v=rφ(x)

(2)

r=0:v=0

(3)

r=l:vx+hv=0

(4)

利用初值问题分离变量法可得到(1)～(4)的形式解为

下面我们首先用分离变量法求解

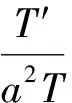
T′+λa2T=0

(5)

X″+λX=0

(6)

先考虑(6).根据边界条件(3),(4),X(r)应当满足边界条件

X(0)=0,X′(l)+hX(l)=0

(7)

对于边值问题(6),(7),讨论可得

(i) 当λ≤0时,只有平凡解X≡0;

(ii) 当λ>0时,

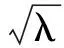
(8)

利用边界条件X(0)=0,得A=0.于是由(7)的第二个边界条件得到

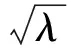
(9)

为使X(r)为非平凡解,λ应满足

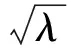
(10)

即λ应是超越方程的正解:

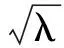
(11)

令

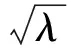
(12)

则式(11)变为

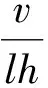
(13)

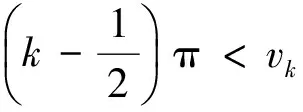
(14)

及相应的固有函数

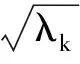
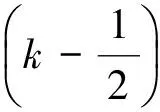
(15)

把λ=λk代入方程(5),可得

Tk(t)=Cke-a2λkt(k=1,2,3,…)

(16)

于是得到一列可分离变量的特解

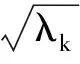
(17)

由于方程(1)及边界条件(3),(4)都是其次的,故可利用叠加原理构造级数形式的解

(18)

由(3)为使t=0,v(r,t)=φ(r)r应成立.

(19)

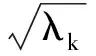
设固有函数Xn和Xm分别对应于不同的固有值λn和λm,即

以Xm和Xn分别乘上面第一和第二式,相减后在[0,l]上积分,利用Xn和Xm都满足边界条件(3),(4),就得到

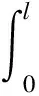
由于λn≠λm,故得固有函数系的正交性:

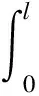
(20)

记

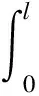
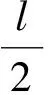
(21)

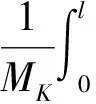
(22)

将它代入(18)式,就得到初边值问题(1)～(4)的形式解为

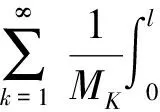
(23)

定理2 形如(1)～(4)柯西问题在有界函数类中的解是唯一的,而且连续依赖于所给的初始条件.

证明先证明有界解的唯一性.假设柯西问题(1)～(4)有两个有界解v1及v2,则其差为v=v1-v2仍满足(1)～(4)及零初始条件v(r,t)=0 (0≤r≤∞),我们证明,在整个区域t≥0, 0≤r≤∞上v≡o.尽管函数v是有界的:|v|≤2B,但由于区域是无界的,函数v(r,t)可能在任何地方都达不到它的最大值与最小值,因此我们不能直接应用前面的极值原理.

为了应用极值原理来证明唯一性,对于上半平面的任何一点(r0,t0),t0>0,我们考虑下面的矩形区域

R0:0≤t≤t0,|r-r0|≤L

其中L是一个任意给定的正数.作函数

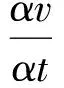
W(r0±L,t)=2B≥v(r0±L,t)

因此在R0的下底及侧边上成立着不等式

W(r,t)≥v(r,t)

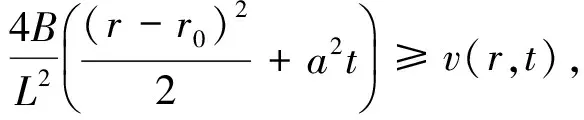
下面我们证明柯西问题的有界解对初始条件的连续依赖性.为此,只需证明当|φ=(x)|≤η时,在整个区域t≥0,0≤r<∞上|v(r,t)|≤η.

同样考虑第一象限任一点(r0,t0),t0>0

R0:0≤t≤t0,|r-r0|≤L,

其中L是一个任意给定的正数.

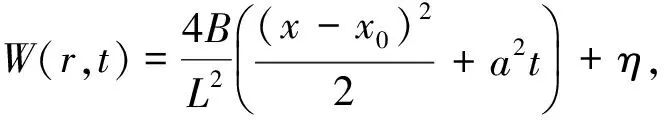
W(r0±L,t)=2B≥v(r0±L,t)

因此在R0的下底及侧边上成立着不等式W(r,t)≥v(r,t),于是由定理2.1知在区域R0上也成立着W(r,t)≥v(r,t),即

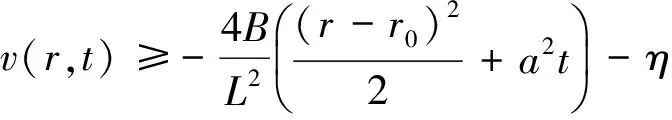
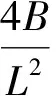
(24)

v(r,0)=rφ(r)=Ψ(r)

(25)

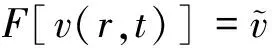
(26)

由(25)得到

(27)

解带参数λ的常微分方程的柯西问题.它的解为

(28)

函数e-a2λ2t的傅里叶变换为:

利用复变函数的积分计算知

利用性质 2 ,f1(x)和f2(x)的卷积的傅里叶变换等于f1(x)和f2(x)的傅里叶变换的乘积,即F[f1*f2]=F[f1]·F[f2].由(28)可得到柯西问题(24)～(25)的解为

并记

(29)

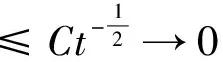
其中C为一个仅与a及‖Ψ‖L′(R)有关的正常数

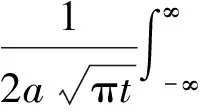
傅里叶变换的应用提出了许多需要在数学上认真加以研究的问题,这当中的不少问题在广义函数论和傅里叶分析理论中得到了解答,同时它为解方程提供了新思路,成为用来的解方程的有力工具.

[1] 谷超豪, 李大潜, 陈恕行,等. 数学物理方程[M]. 2版. 北京: 高等教育出版社.

[2] Evans L C. Partial Differential Equations[M]. New York, Proc of AMC,1998.

[3] 丁同仁, 李承治. 常微分方程教程[M]. 2版. 北京: 等教育出版社.

[4] 华东师范大学数学系. 数学分析[M]. 上册, 3版. 北京: 高等教育出版社.

[5] 华东师范大学数学系. 数学分析[M]. 下册, 3版. 北京: 高等教育出版社.

[6] 郇中丹, 黄海洋. 偏微分方程高[M]. 北京: 高等教育出版社.

[7] 张恭庆, 林源渠. 泛函分析讲[M]. 上册. 北京: 北京大学出版社.

[8] 张恭庆, 林源渠. 泛函分析讲[M]. 下册. 北京:北京大学出版社.

[9] 程其襄, 张奠宙, 魏国强, 等. 实变函数与泛函分析基础[M]. 2版. 北京： 高等教育出版社.

[10] 陈昌平, 许明, 王学锋, 等. 数学物理方程[M]. 北京: 高等教育出版社,1989.

[11] 姜礼尚, 陈亚浙, 刘西垣, 等. 数学物理方程讲义[M]. 2版. 北京: 高等教育出版社,1996.

StudyontheSolutionoftheThree-dimensionalHeatConductionEquationwithSphericalSymmetry

QIAN Jing-yi, LI Tong-xing

(School of Applied Mathetics, Nanjing University of Finance and Economics, Nanjing Jiangsu 210023, China)

In this paper,we solved for the three-dimensional heat conduction equation with spherical symmetry, and analyzed to prove the uniqueness, stability, progressiveness of the solution, Fu Liye transform method was given to the corresponding equation.

uniqueness; stability; progressiveness; fourier transform

2012-10-16

钱镜伊(1988-), 女, 江苏宿迁人, 硕士研究生, 研究方向为数学金融学.

O175

A

1671-6876(2013)01-0015-06

[责任编辑李春红]