基于广义梁理论的薄壁圆柱壳稳定性分析

谭福颖 乔 玲 韩晓林

(东南大学土木工程学院,南京 210096)(东南大学江苏省工程力学分析重点实验室,南京 210096)

壳体结构在航空航天工程和土木工程中得到了广泛应用,而圆柱壳屈曲问题一直是壳体研究中最为关注的课题之一,这类结构在承受荷载时大多在强度破坏前就已发生失稳破坏,因此研究影响薄壁壳体稳定性的因素一直受到研究者们的重视.

对于广义梁理论,国内外学者进行了大量研究.1989年德国学者Schardt[1]首次提出广义梁理论,此理论是在经典的Vlasov梁理论的基础上进行拓展,通过研究局部坐标系下平面弯曲截面下变形,从而分析全局域和局部域下薄壁棱柱形矩形结构构件的屈曲行为.由于Schardt的研究成果主要以德文的形式发表,在一定程度上影响了该理论的传播和应用.Davies等[2]最先以英文的方式将广义梁理论进行阐述,并应用该理论对冷弯薄壁型钢(主要是C形和Z形截面)的相关屈曲进行了系统的理论分析和试验验证.文献[3-7]将广义梁理论扩展到多种材料形式、考虑剪切扭转变形、几何非线性、一阶静力和二阶稳定以及任意分支开口截面下的薄壁杆件分析中,并给出了广义梁有限元模型以及利用数值计算方法求解出了广义梁方程.我国学者李开禧[8]1990年提出过类似的理论,研究在中线为直线的假定条件下,利用图解法求解薄壁杆件的截面变形问题.与国外相比,国内对于广义梁理论这种充分考虑截面变形梁理论的研究仍然滞后,国内相关的研究鲜有报道.

本文将广义梁理论引入并推广到薄壁圆形截面柱壳的稳定性分析中,开展了对中空薄壁圆柱壳屈曲的研究,从一阶线性分析拓展到各阶屈曲分析,通过获得屈曲应力和与之对应的临界轴长表达式,研究了不同长细比下临界应力随轴长、厚度的变化关系,为薄壁圆柱壳稳定性分析提供了一个新方法.

1 薄壁圆柱壳稳定性理论分析

1.1 几何方程

如图1所示,全局坐标系XYZ中,圆柱壳半径为r,厚度为t,轴长为L.在中性面上建立一个局部坐标系x,θ和z.其中轴向x∈[0，L],圆周向θ∈[0，2π],径向z∈[-t/2，+t/2].分别用u,v,w表示局部坐标系下点的各向位移.

图1 全局坐标系及局部坐标系下圆柱壳参数示意图

基于Love-Kirchhoff 假设和薄壳理论,应变位移关系为[9]

(1)

由经典梁理论可知,中性横截面上任一点位移可表示为截面位移与截面翘曲的组合,因此u,v,w可表示成

(2)

式中,x,θ为独立的自变量和位移振幅函数;φk(x)表示截面翘曲程度;位移函数uk(θ)表示在同一截面上的截面轴向位移.将式(2)代入式(1),根据线性应变和非线性应变的定义,将应变划分为与截面位移u,v,w成线性关系的线性应变,以及与截面位移u,v,w成非线性关系的非线性应变2部分.整理得

(3)

(4)

1.2 能量变分方程

薄膜应变能U可通过由薄膜内力在中面薄膜变形中所做内功计算而得.取微分单元体,由其薄膜力的元功可得能量变分方程为

(5)

(6)

其中,Q11=Q22=E/(1-ν2),Q12=νQ11,Q33=G，E为弹性模量,v为泊松比.

(7)

(8)

壳体稳定性分析的首要问题是临界荷载问题,而该问题是由前屈曲平衡性态来决定的.当壳体进入屈曲状态,会出现非线性薄膜应力,使之偏离到屈曲后附加状态,即非线性状态,但附加状态偏离屈曲状态的位移无限小,因此,非线性项应变可以忽略不计.故而,在忽略非线性应变前提下,将上述各式代入到能量变分方程(5)中，可得

(9)

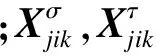
由以上分析可知,能量泛函δU是一个只与轴向u(x,θ)有关的函数,求解u(x,θ)的表达式即可得到各未知参量.由于u(x,θ)可以分解为2个正交函数uk(θ)和φk(x)的乘积,因此问题归结为求解uk(θ)和φk(x)的表达式.

1.3 各阶屈曲模态

根据uk(θ)和φk(x)的正交性可知,位移函数中u(x,θ)中位移振幅函数φk(x)表示截面翘曲程度,uk(θ)表示在同一截面上的截面位移,因此获得uk(θ)即可得到壳体横截面屈曲模态.

由广义梁理论可知,若要求解能量泛函δU,矩阵Cik,Bik必须对角化.矩阵Cik,Bik对角化，即为uk,uk,θθ,uk,θθθθ满足独立正交[11]条件,可表示为

(10)

由正交条件可知，uk(θ)可用三角周期函数表示为

uk(θ)=rsinkθ,uk(θ)=rcoskθ

(11)

对应于一个给定的k值,uk有正弦和余弦函数2种表达形式,且两者相互正交.由工程实际可知,相同的屈曲载荷下由于位移分叉存在2种形态类似的屈曲模态.引入同一屈曲波数m可对应于不同的阶数k值,得到2种相似的屈曲模态.因此,当表达式设为正弦函数时,k=2m;设为余弦函数时,k=2m+1.因此,筒壳各阶截面位移表达式为

(12a)

(12b)

图2为薄壁圆柱壳2阶～13阶模态.由图可知,在同一屈曲载荷下由于位移分叉存在2种形态类似的屈曲模态,如2阶、3阶同为屈曲模态,4阶、5阶同为扭转模态等,也再次证明所假设的正交对称位移函数是可取的.

此外,在实际工程中需要考虑轴向变形和前屈曲问题时,必须要得到其轴向变形模态.对比轴向压缩模态的力学性质不难发现,在发生压缩模态时,只存在轴向位移.因此有

ue=1,ve=0,we=0

(13)

式中,下标e表示轴向伸缩模态下的位移分量.结合式(12)可以得到,当m=0时，第1阶轴压模态为

m=0,k=1,u1=1,v1=0,w1=0

(14)

图2 薄壁圆柱壳各阶屈曲模态

柱壳屈曲时会产生此模态.因此,各阶模态还必须包含一个轴对称模态(用下标a表示),其各位移分量为

ua=0,va=0,wa=1

(15)

ut=0,vt=r,wt=0

(16)

变形图如图3(c)所示.至此,通过分析获得了所有可能的屈曲模态和相应的位移函数uk(θ)的表达式.因此,下面的研究目标是位移振幅函数φk(x)的表达式.

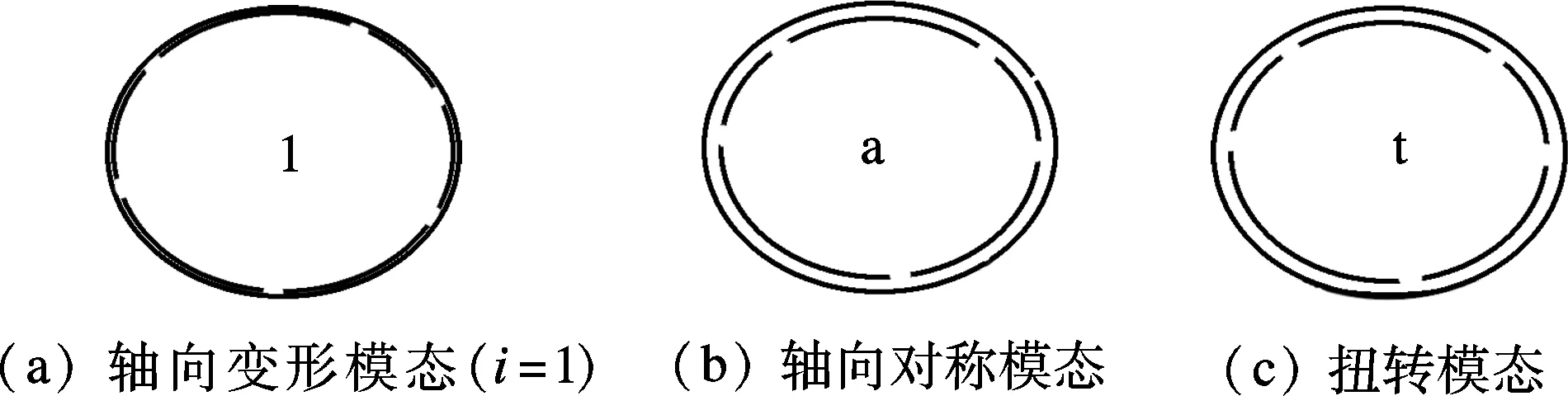
图3 变形图

1.4 特征值函数

在广义梁理论中,通过特征值求临界屈曲应力[10]有Galerkin法和有限元法.本文为了求解薄壁圆柱壳的能量变分方程,采取Galerkin方法[11],由边界条件决定位移振幅函数φk(x)的表达式,从而获得能量变分方程的特征值函数,进而求得临界屈曲应力.

1) 边界条件为简支、特征值函数为三角函数形式.其位移振幅函数可以设成

(17)

式中,dk为第k阶模态的振幅(可由具体问题给出);n为纵向半波数;L为结构的轴向长度.

2) 边界条件为非简支.位移振幅函数可以设成[12]

(18)

本文主要研究均匀压缩下的简支薄壁圆柱壳的稳定性问题,因此,变分方程(9)变形为

(19)

整理后,特征值方程为

式中,λb为分叉屈曲下的特征值,并且只与轴向坐标L有关.将位移振幅函数代入式(20),分叉屈曲特征值λb为

(21)

(22)

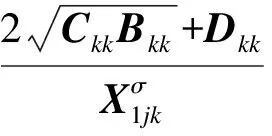
(23)

(24)

(25)

2 薄壁圆柱壳稳定性数值仿真

通过理论推导已得到临界应力的表达式,因此,为了验证此方法的适用性和正确性,下文将针对具体算例,采用理论方法与数值解法进行对比,研究轴长和厚度对屈曲应力的影响.

2.1 构件尺寸比

当构件半径和厚度为定量,随着轴长的不断增长,构件可划分为极短柱壳、中短柱壳和细长柱壳3类.本文以均匀压缩圆柱壳为研究对象,已知圆柱壳中心截面半径r=100 mm,厚度t=1 mm.采用铝合金材料,弹性模量E=68 GPa,泊松比ν=0.33,柱顶受到1 600 N的均匀轴向荷载,两端简支.

由文献[14]可知,当L≤17.37 mm时,构件属于极短柱壳;当L>17.37 mm时,构件属于中短柱壳；当L>1 004.30 mm时,构件属于细长柱壳.

2.2 圆柱壳轴长与屈曲应力的关系

基于以上理论分析,简支边界条件下的正弦振幅函数为φk(x),分别令纵向半屈曲波数n=1,2,得到屈曲应力σb和轴长L的关系如图4所示.

分析图4中n=1的情况可知:

1) 当轴长L<17.37 mm时,主要的屈服模态以轴对称模态的形式出现,此时只有径向位移,屈曲模态如图3(b)所示.由构件细长比可知,构件为极短圆柱壳.极短圆柱壳下临界屈曲应力值和对应的临界轴长为[15-16]

图4 屈曲应力σb和轴长L关系图

2) 当轴长17.37

3) 当轴长L>1 000 mm,构件为细长圆柱壳,屈曲应力σb随着轴长L的增长不断减小,主要以挠曲模态(m=1)的形式发生屈曲.

结合n=1和n=2的情况可得:

1) 由图4可知当纵向半屈曲波数n=2和n=1,屈曲应力σb随着轴长L的变化趋势完全一致,因此,n=2与n=1相比,相当于整体图形在横坐标方向平移一段距离.

(2) 当L<100 mm,屈曲应力存在2个相等极小值点,分别对应于轴对称模态;当1001 600 mm时,构件只以挠曲模态(m=1)的形式发生屈曲.

2.3 壁厚与屈曲应力的关系

在2.2节中已研究了由圆柱壳轴长L引起的屈曲应力σb变化趋势,而影响圆柱壳稳定性的因素往往还有构件的厚度t.由于本文研究对象为薄壁圆柱壳,厚度t取为1～5 mm,其他参数不变,边界条件仍为两端简支.此外,采用有限元软件建模,得到相应条件下圆柱壳的屈曲承载力值,与本文方法对比结果如表1所示.

表1 3种柱壳随厚度变化的屈曲承载力 N/mm

由表1可知,随着厚度的增加,屈曲承载力整体呈增大趋势.在一定范围内,增大厚度能够提高结构的稳定性.通过本文推导方法所得的理论解和有限元计算结果进行对比可知,极短和中短圆柱壳屈曲承载力误差在2%～3%之间,细长柱壳的误差稍微偏大,但也小于5%,其主要原因可能是由于细长柱壳屈曲受圆周波数的影响.极短柱壳屈曲承载力增长幅度为三者中最大,此时厚度对于提高结构稳定性的作用最为明显.对比于细长柱,厚度对细长柱的屈曲承载力的影响相对较小.

3 结语

基于广义梁理论研究了薄壁圆柱壳稳定性分析方法,并采用该方法研究了轴长和厚度对屈曲应力的影响.在数值仿真中,极短圆柱壳主要以轴对称模态的形式发生屈服,存在极小值.中短圆柱壳的屈曲主要发生在圆周波数m在2～10区段内,屈曲应力σb随着轴长L的增长整体呈现下降的趋势,其中也存在几个局部极小的屈曲应力.细长圆柱壳主要以挠曲模态(m=1)的形式发生屈曲,屈曲应力σb随着轴长L的增长不断减小.另外,在厚度变化的情况下,厚度对极短圆柱壳的影响为三者中最大,其次为中短圆柱壳,最后为细长圆柱壳.但总体来说,一定范围内,随着厚度的增加,屈曲承载力都相应增加.因此,在一定范围内,通过增加厚度提高构件的屈曲承载能力也是显而易见的.通过与已有文献结论、有限元分析的结果对比,证明了将广义梁理论推广到圆形截面进行屈曲分析是可行的,而且计算精度较高,与已有结果保持较好的一致性,这对薄壁圆柱壳稳定性分析提供了一个新的方法途径.

)

[1] Schardt R.Verallgemeinertetechnischebiegetheorie[M]. Berlin: Springer, 1989.

[2] Davies J M, Leach P, Heinz D. Second-order generalized beam theory [J].JournalofConstructionalSteelResearch, 1994,31(2/3): 221-241.

[3] Silvestre N. Generalised beam theory to analyze the buckling behavior of circular cylindrical shells and tubes [J].Thin-WalledStructures, 2007,45(2): 185-198.

[4] Ranzi G, Luogo A. A new approach for thin-walled member analysis in the framework of GBT [J].Thin-WalledStructures, 2011,49(11): 1404-1414.

[5] Dinis P B, Camotim D, Silvestre N. GBT formulation to analyse the buckling behaviour of thin-walled members with arbitrarily ‘branched’ open cross-sections [J].Thin-WalledStructures, 2006,44(1): 20-38.

[6] Basaglia C, Camotim D, Silvestre N. Global buckling analysis of plane and space thin-walled frames in the context of GBT [J].Thin-WalledStructures, 2008,46(1): 79-101.

[7] Basaglia C, Camotim D, Silvestre N. Post-buckling analysis of thin-walled steel frames using generalised beam theory (GBT) [J].Thin-WalledStructures, 2013,62: 229-242.

[8] 李开禧. 弹性薄壁杆件的翘曲[M]. 北京:中国建筑工业出版社,1990.

[9] Ju G T, Kyriakides S. Bifurcation and localization instabilities in cylindrical shells under bending-Ⅱ： predictions [J].InternationalJournalofSolidsandStructures, 1992,29(9): 1143-1171.

[10] Camotim D, Silvestre N, Goncalves R,et al. GBT-based structural analysis of thin-walled members: overview, recent progress and future developments [J].EngineeringStructures,MechanicsandConstruction,SMCD, 2006,14-17: 187-204.

[11] Silvestre N, Camotim D. GBT buckling analysis of pultruded FRP lipped channel members [J].ComputerandStructures, 2003,81(18/19): 1889-1904.

[12] Silvestre N, Camotim D. Distortional buckling formulae for cold formed steel C and Z-section members: part Ⅰ-derivation [J].Thin-WalledStructures, 2004,42(11): 1567-1597.

[13] Singer J, Arbocz J, Weller T.Bucklingexperiments-experimentalmethodsinbucklingofthin-walledstructures[M]. New York, USA: Wiley, 2002.

[14] 陈兴华,龙连春.轴压薄壁圆柱壳弹性失稳承载力分类及对比[C]//北京力学会第15届学术年会论文摘要集.北京,2009:215-216.

Chen Xinghua, Long Lianchun. Thin-walled cylindrical shells’ elastic buckling bearing capacity of classification and comparison with axial compressive [C]//MechanicsofBeijingtheFifteenthAnnualMeetingofAbstracts. Beijing, 2009:215-216.(in Chinese)

[15] Timoshenko S P, Gere J M.Theoryofelasticstability[M]. New York, USA: McGraw-Hill, 1961.

[16] Brush D O, Almroth B O.Bucklingofbars,platesandshells[M]. New York, USA: McGraw-Hill, 1975.