船-桥碰撞力理论分析及复合材料防撞系统

刘伟庆 方 海 祝 露 韩 娟 吴志敏

(南京工业大学先进工程复合材料研究中心,南京211816)

船-桥碰撞事故往往会造成桥损、船毁、人亡、航道受阻、陆上交通中断以及货物泄漏等严重后果,重建桥梁和疏通航道的费用十分惊人.因此,近年来关于船-桥碰撞机理及桥梁防撞系统的研究得到越来越多的关注.国内外关于船-桥碰撞机理的主要研究方法包括试验研究法[1]、简化分析法[2-4]和有限元仿真法[5-6].其中,简化分析法使用方便,能够基本把握船撞桥的碰撞力和结构动力反应.现有研究大多是基于等效静力的方法,忽略了船-桥碰撞过程中的动力因素.我国近年来在大桥桥墩中常用的防撞设施为钢结构形式,具体为钢套(浮)箱、钢围堰、钢丝绳复合吸能防撞圈等.针对该类防撞设施,陈国虞[7-9]等采用有限元动力分析软件,研究了钢结构防撞设施在船舶撞击过程中的塑性变形破损消能行为.

本文综合考虑桥墩刚度及上、下部结构对桥墩的约束作用等因素,建立船-桥碰撞简化动力学模型,进行理论分析求解,并提出基于船-桥碰撞接触时间的船撞力计算公式.此外还提出了大型复合材料防船撞系统的设计理念,阐述了其结构构造与冲击试验结果,并介绍了设置复合材料防撞系统的典型桥梁工程应用,可供相关工程实践参考.

1 船-桥碰撞动力学机理

1.1 简化动力学模型

本文提出了一种由被撞击桥墩和相邻2个半跨组成的半跨单墩模型,将桥梁上部结构等效为1个具有一定质量M的实体作用在桥墩顶部.考虑桥墩截面特性的变化,将桥墩沿轴线方向划分为n个具有一定质量、刚度的梁单元.船-桥碰撞过程中桥墩下部地基与基础的弹性变形会吸收一部分的碰撞能量,对碰撞力有不可忽视的影响,因此采用弹性约束刚度为k1的抗推弹簧、弹性约束刚度为k2的竖向弹簧和弹性约束刚度为k3的抗转动弹簧来考虑基础及土层对桥墩的约束作用.用一个刚度为Kb的非线性弹簧来模拟船艏,一个单自由度的质量块来模拟船舶的质量mb,借助非线性弹簧将质量块与桥墩在撞击点耦合.采用附加质量模型来计入周围流体对船-桥碰撞的影响.

综上所述,本文提出的船-桥碰撞简化力学模型如图1所示.图中,v0为船舶撞击速度,x为桥墩单元的轴线坐标,l为桥墩高度,li为第i个桥墩单元的桥墩高度,P(x,t)为横向分布荷载,y(x,t)为桥墩横向位移函数,t为时间变量.

1.2 船艏刚度

船艏结构的碰撞特性是影响船-桥碰撞过程的关键因素之一.本研究组近期开展了各类代表性船舶撞击刚性墙的数值模拟,以期得出船艏刚度与阻尼模型.已有研究表明,撞击角度、被撞结构的形状和几何尺寸,均会影响船舶撞击力.为了建立具有一定普遍适用性的船艏刚度模型,将桥墩结构简化为刚性墙壁,针对有无球鼻艏船舶正撞、侧撞桥墩以及桥墩截面为方形、圆端形、尖形等多种工况进行研究.以5 000 t级船舶为例,其碰撞模型见图2.通过大量有限元模拟,研究尖形桥墩的夹角θ以及圆端形桥墩半径R对船舶撞击力和船艏刚度及阻尼的影响.

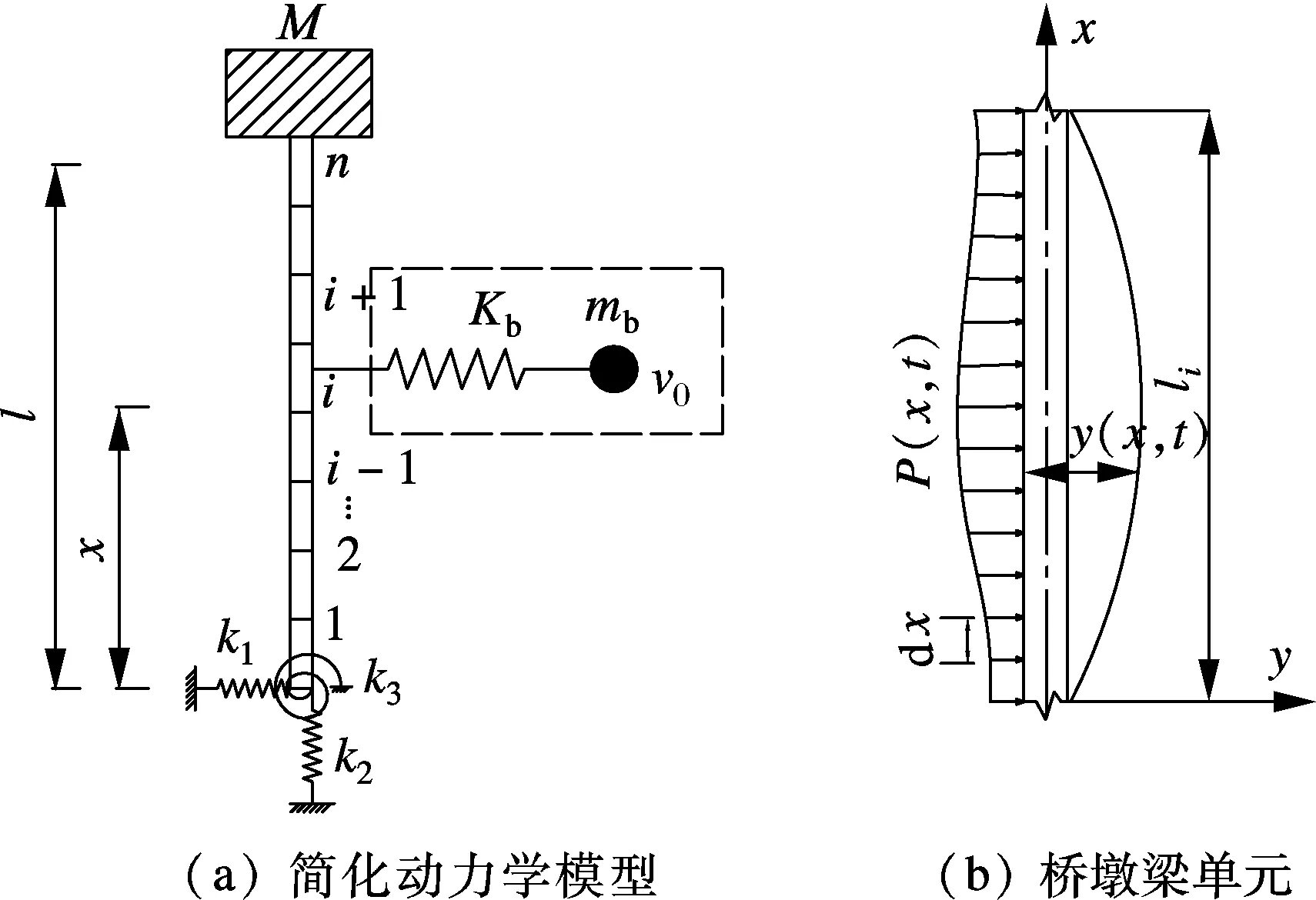
图1 船-桥碰撞分析模型

图2 船撞有限元模型

由撞击过程中撞击力F与船艏撞深δ之间的关系,可建立简单合理的船艏刚度模型.根据5 000 t级船舶正撞26组平面刚性墙计算结果,可采用分段函数的形式表示船舶的F-δ关系曲线.撞击前半段采用指数函数近似描述,后半段采用直线关系近似描述(见图3).5 000 t级船舶船艏刚度的简化模型为

(1)

式中,X′为分段拟合曲线的交点;X为最大撞深.

图3 撞击力-撞深关系曲线

1.3 船-桥碰撞动力方程

考虑桥墩梁单元的弯曲变形、剪切变形以及转动惯量的作用,基于分布质量的弹性体理论,等截面桥墩单元的偏微分运动方程为

(2)

式中,E为弹性模量；I为惯性矩；N为轴向压力;ρ为桥墩材料密度;κ为常数因子;A为桥墩单元的横截面面积;G为剪切模量.

式(2)可改写为

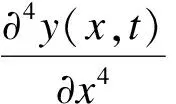
(3)

式中,a1，a2，a3，a4为系数.

对式(3)进行Laplace变换,综合桥墩边界条件和撞击工况,建立船-桥碰撞系统的整体矩阵方程.借助Durbin逆变换方法,并结合Matlab软件对频域内的动力响应进行数值反演,得出时域内的船-桥撞击力为

(4)

式中,T为所要计算的总时间;N′为输出数值的时间间隔.数值反演时由像函数F(s)求像原函数f(t),其中s=a+iω,ω∈R,a为位于F(s)所有奇点右方的任意值.求解时首先要确定a,N′和T.一般而言,aT在5～10之间取值,N′在50～5 000之间取值,即可得到较满意的结果.

1.4 桥-船相对刚度对峰值撞击力的影响

图4为给定工况下(船舶质量为200 t,撞击速度为3 m/s),船舶刚度Kb=5,10,15 MN/m时峰值撞击力FBm与桥-船相对刚度(即桥墩与船艏的刚度比值)Kp/Kb之间的关系,其中Kp为桥墩刚度.由图可知,当Kp/Kb<50时,峰值撞击力随桥-船相对刚度的增大呈对数形式增大;当Kp/Kb>50时,随桥船相对刚度的增大,峰值撞击力几乎保持不变.

桥船相对刚度为50时,按照本文方法与欧洲统一规范方法[10]求解的峰值撞击力比较结果见表1.由表可知,Kp/Kb=50时,按2种方法求解的峰值撞击力较接近.结合图4,当Kp/Kb>50时,船-桥碰撞过程可近似看成是船舶撞击刚性体的过程,峰值撞击力可近似按欧洲统一规范取值.

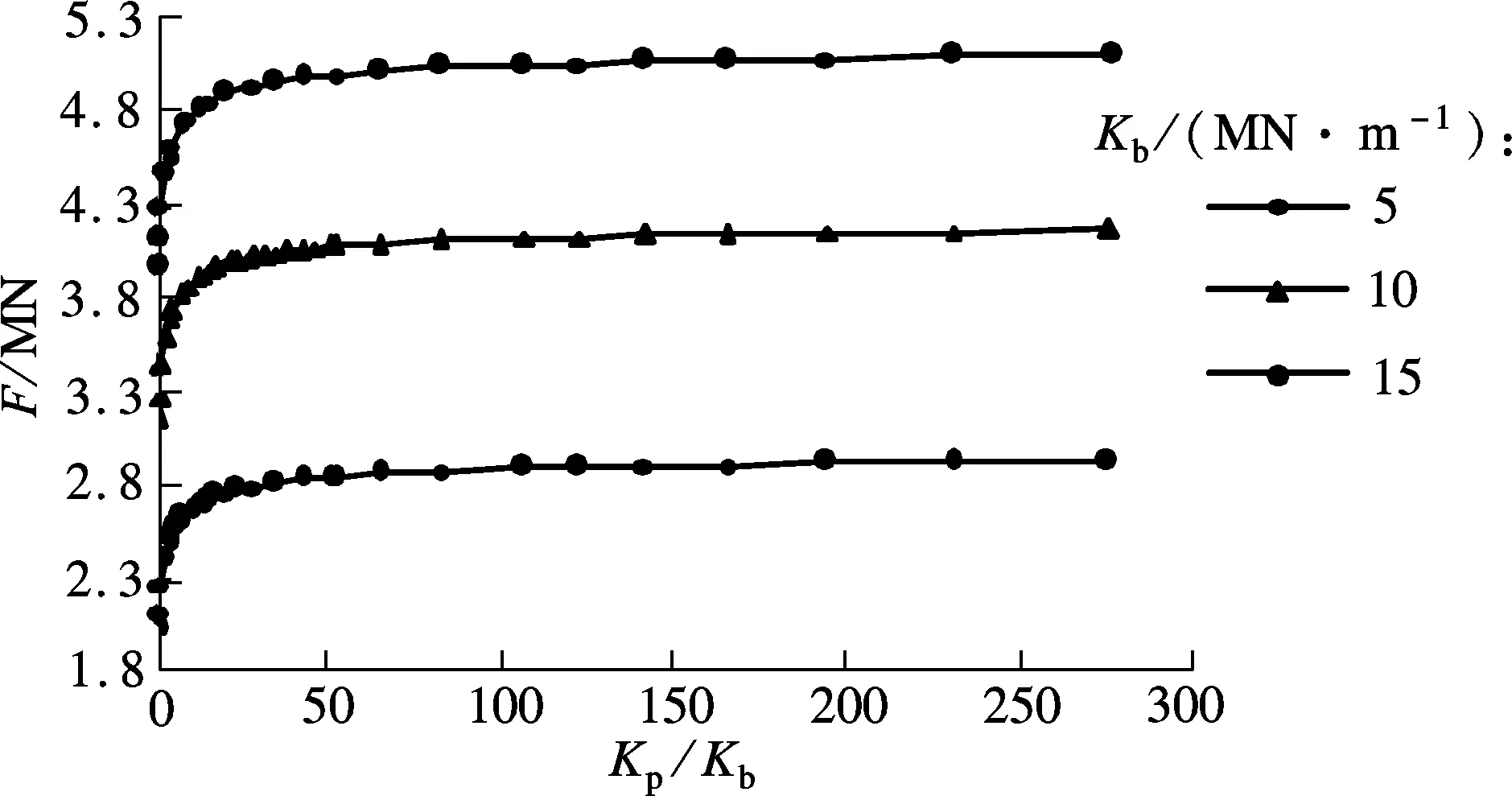
图4 桥-船相对刚度对峰值撞击力的影响

表1 峰值撞击力比较(mb=200 t, v0=3 m/s, Kp/Kb=50)

1.5 基于碰撞接触时间的峰值撞击力公式

由冲量定理可知,船-桥碰撞接触时间的长短直接影响撞击力的大小,因此可由式(4)进一步分析船舶质量、船舶速度、船舶刚度等参数与碰撞接触时间tc的关系.图5为tc拟合前后的对比图,拟合曲线的相关系数为0.966 032,拟合公式为

(5)

图5 碰撞接触时间拟合前后的对比

由式(5)可知,《公路桥涵设计通用规范》[11]中漂流物碰撞接触时间单纯取1 s是不合理的,而该规范中漂流物撞击力的计算公式为

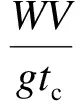
(6)

式中,W为漂流物质量;V为撞击速度;tc为撞击时间;g=9.81 m/s2为重力加速度.

将式(5)代入式(6),可得撞击力为

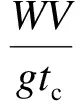
(7)

由式(7)求得的撞击力为平均撞击力.峰值撞击力约为平均撞击力的2倍[12],因此峰值撞击力为

(8)

2 复合材料防撞系统

2.1 桥梁防撞的基本原理

设置桥梁防船撞系统的目的是防止因船舶撞击力超过桥墩的设计承受能力,船舶撞击桥墩时桥梁发生整体或局部破坏.采用不同类型的防撞设施,可以阻止船舶撞击力传到桥墩,或者通过缓冲消能延长碰撞接触时间,从而减小船舶撞击力,保障桥梁安全.防撞设施的设计需要考虑桥墩自身抗撞能力、桥墩位置、桥墩外形、水流速度、水位变化情况、通航船舶类型、碰撞速度等各类因素.

2.2 现有防撞系统分类

经过多年研究应用,已形成多种类型的桥梁防撞设施,其基本原理都是基于能量吸收与动量缓冲的.具体而言,防撞设施可分为如下两大类[13]:① 间接式防撞设施.其特点为,在桥墩之外另设防撞设施,桥墩不直接受力,如桩群方式、薄壳筑沙围堰方式、人工岛方式等,一般用于水浅、地质情况较好的场合.该类方法虽然一劳永逸,但会影响航道,且常因为造价太高或者条件不具备而放弃.② 直接式防撞设施.力经过缓冲后直接作用在桥墩上,如护弦方式、缓冲材料设施方式、缓冲设施工程方式及固定或浮式钢套箱防撞设施等.一般使用在航道较窄、水较深的场合,通常建造费用较省,土建工程量不大.

2.3 复合材料防撞系统的基本构造

作为能量吸收元件,纤维增强复合材料结构要比一些常用的金属结构具有更高的能量吸收能力,且压溃载荷分布均匀[14-16],已在航天、航空、汽车和运动器材等防护装置方面得到越来越广泛的应用.

针对传统防撞设施存在的刚性大、易腐蚀等缺陷,基于纤维增强复合材料耐腐蚀、轻质高强、缓冲性能优异等特点,本文研制了大型桥梁复合材料防撞系统.该防撞系统为空间格构腹板增强泡沫夹芯复合材料结构(见图6(a)),该结构的格构纤维腹板、泡沫芯材与复合材料面层均为一次成型,具有制备方便、成本较低、整体受力性能好的优点,适合采用真空导入工艺制备大型防撞结构件.图6(a)中,Ws,Wt,Wh分别为腹板间距、腹板厚度和腹板高度.

图6 复合材料防船撞系统结构

考虑桥墩形状、船舶吨位等因素,将格构腹板增强泡沫夹芯复合材料防撞结构设计成各类截面形状和尺寸,如大直径圆型截面复合材料防撞系统(见图6(b)～(c)).

大型桥梁复合材料防撞系统可根据桥墩结构、通航水位等灵活设计成固定式和自浮式结构,防撞系统外壳为强耐腐蚀性且易维护的树脂基纤维增强复合材料,尤其适合于海水腐蚀环境及干湿交替环境.经空间格构腹板增强后的闭孔泡沫芯材具有较高的抗剪强度;玻璃纤维增强复合材料的弹性模量约为钢材的1/10,因而在撞击荷载作用下,具有缓冲大变形的特点,可有效延长船-桥碰撞接触时间,能同时保护桥梁与船舶.

2.4 复合材料防撞结构准静态与冲击试验

2.4.1 准静态压缩试验

本文采用正交试验方案,系统完成了81个格构腹板增强泡沫夹芯复合材料试件的准静态压缩性能试验(见图7),分析了腹板间距Ws、腹板高度Wh、腹板厚度Wt以及聚氨酯泡沫密度Wd等因素对抗压强度、屈服承载力以及能量吸收的影响.典型试件破坏形态为格构腹板屈曲折叠,泡沫压碎.格构增强试件的屈服承载力约为无格构试件的15倍.以某典型试件的力-位移曲线为例(见图8),压缩过程可明显地分为3个阶段:点Fp之前的弹性变形阶段、点Fp至点Fd之间的塑性变形阶段以及Fd点之后压实阶段.其中,Fp为弹性变形阶段与塑性变形阶段的临界点,Fd为塑性变形阶段与压实阶段的临界点.图8中,Sd为点Fd之前力-位移曲线所包含的面积.

图7 准静态压缩试验照片

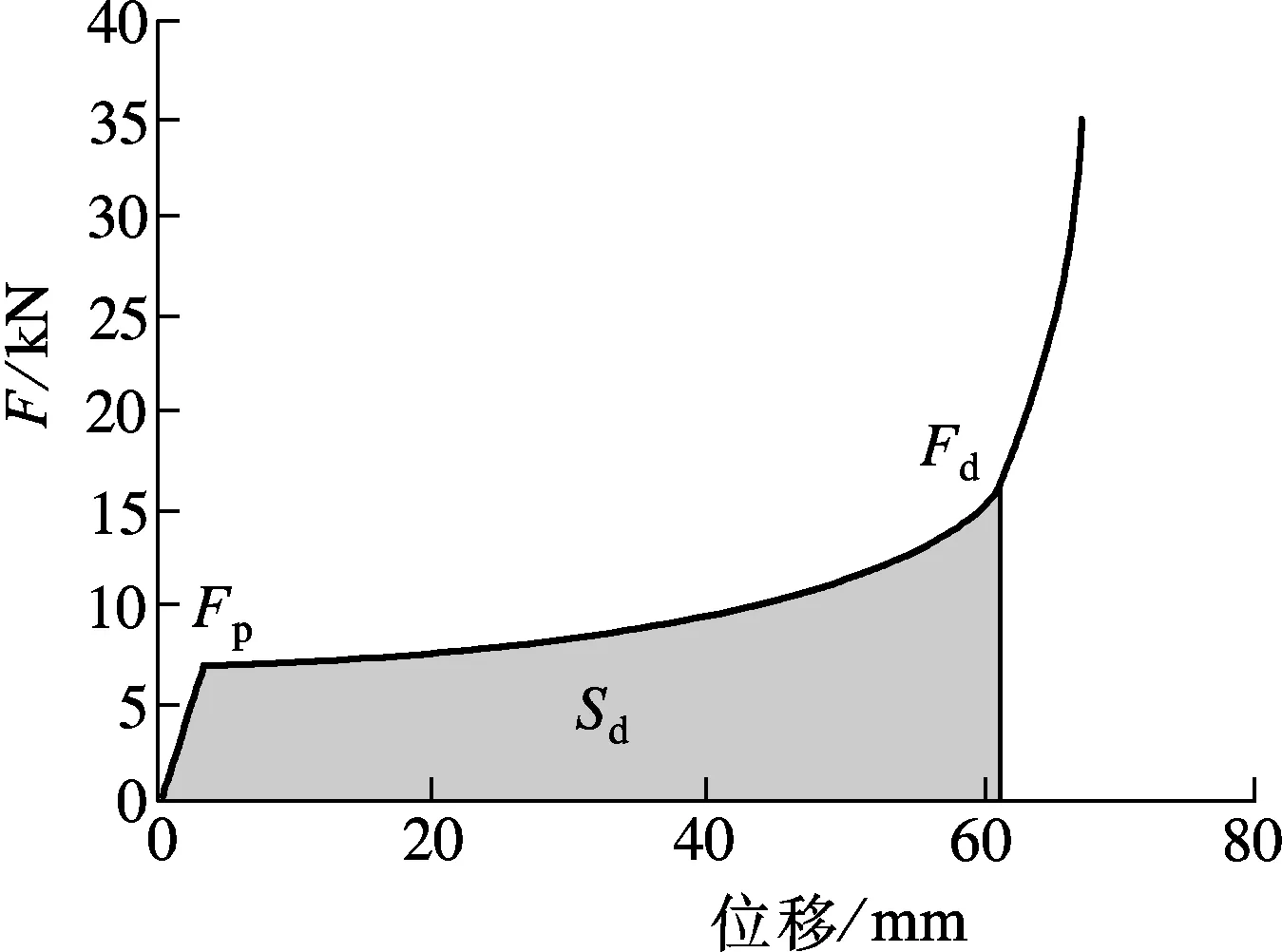
图8 典型试件的力-位移曲线

结合正交试验极差分析,得出各参数对抗压强度和屈服承载力的影响程度由大到小分别为Wt,Ws,Wd,Wh,而对能量吸收影响程度由大到小分别为Wt,Ws,Wh,Wd.因此,腹板厚度和腹板间距是影响试件抗压强度、屈服承载力及能量吸收能力的主要因素,而泡沫密度和腹板高度则是次要因素.

2.4.2 冲击试验

本文针对格构腹板增强泡沫夹芯复合材料板,开展了接触面积较大的撞击性能试验研究.研究了格构腹板间距、腹板厚度等对撞击力削减的影响,并与同尺寸钢构件的撞击性能进行了对比.

设置格构腹板增强复合材料的撞击工况，可将撞击接触时间延长为无防撞工况接触时间的5倍左右;格构腹板增强复合材料试件的撞击接触时间约为无格构腹板增强试件的2倍.无格构腹板增强试件易发生剪切破坏,而格构腹板增强试件无明显破坏,且撞击力大幅减小(见图9(a)).同尺寸钢结构试件利用自身塑性变形来吸收撞击能量,其变形具有不可恢复性,且在撞击瞬间的接触时间未能延长(见图9(b)).由此可知,复合材料结构具有良好的耐撞性能,适合用于防撞消能领域.

图9 试件撞击力时程曲线

3 工程应用实例

本文提出的复合材料防撞系统于2011年6月首先在福州乌龙江大桥上成功应用.该桥已遭受多次船舶撞击事故,主体结构完好无损,有效验证了该防撞系统的有效性.目前,本研究组已建成了润扬长江大桥等6项防船撞工程,正开展港珠澳大桥、马鞍山长江公路大桥等100余项防撞设计,有效促进了我国桥梁工程复合材料防船撞产业的形成,开辟了纤维增强复合材料应用的新领域.

图10(a)为大尺寸复合材料防撞节段的真空导入一次成型工艺照片;图10(b)为乌龙江大桥自浮式复合材料防撞系统照片;图10(c)为常溧线运河桥承台固定式复合材料防撞系统照片;图10(d)为广深高速沿江大桥自浮式复合材料防撞系统照片.该复合材料防撞系统结构新颖、材料先进、耐腐蚀、使用寿命长、易维护,能有效地降低船-桥撞击力,减轻船舶受损程度,具有较高的技术经济优势.

图10 复合材料防船撞系统实例照片

图11为润扬长江大桥北汊斜拉桥自浮式圆形截面复合材料防船撞系统的安装过程照片.防撞节段之间创新性地采用插销式凹凸榫卯连接,有效克服了复合材料的连接难题.通过数值模拟方法系统研究了主塔的船舶撞击力,3 000 t级船舶(v0=3 m/s)的船艏部分与下塔柱发生碰撞,最大撞击力为19.95 MN;而设置D350筒型防撞设施(直径3.5 m)后,桥墩受到的撞击力削减为13.16 MN,接触时间由1.0 s延长至1.3 s(见图12).本防撞系统的防护范围较大,船尖不会对混凝土墩身造成局部撞损;同时,复合材料缓冲性能可有效减轻船舶受损程度.

图11 自浮式圆形截面复合材料防撞系统实例照片

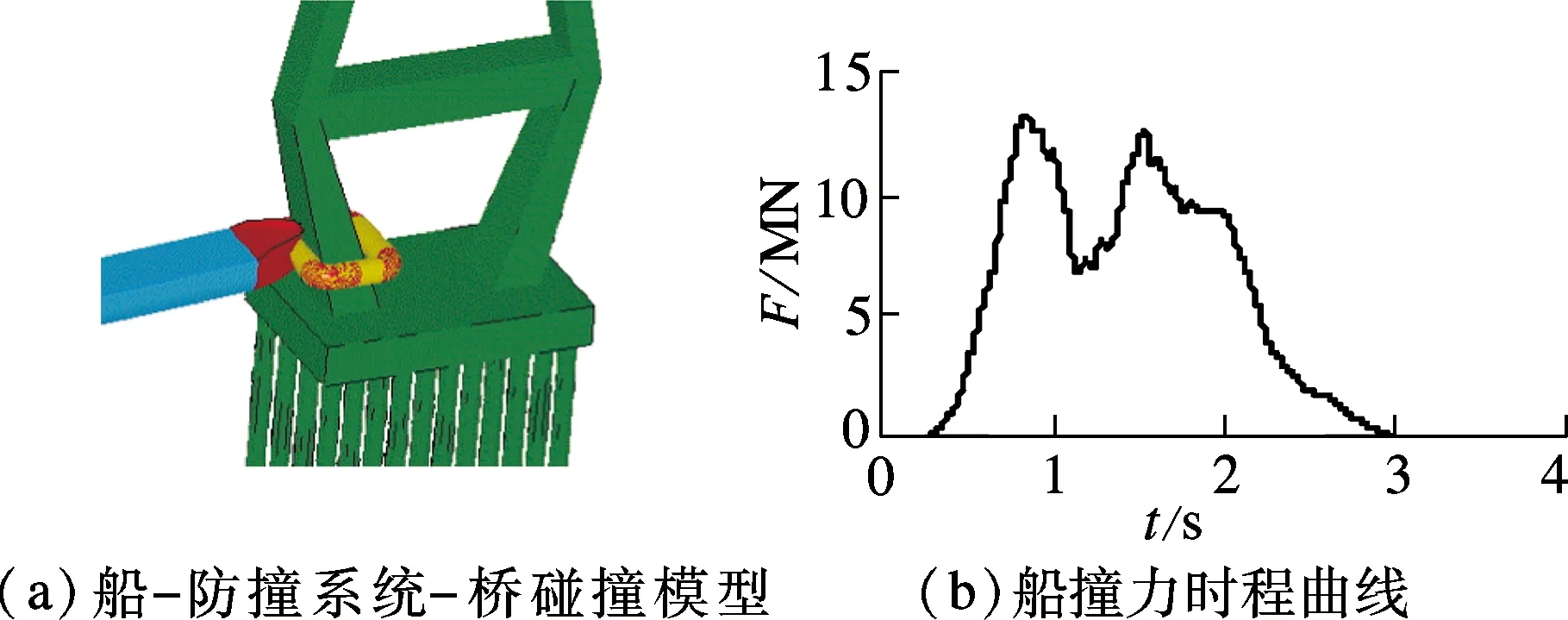
图12 船-桥碰撞有限元数值模拟

4 结论

1) 采用分段函数的形式来表示代表性船舶的船艏撞击力-撞深关系曲线.撞击前半段采用指数函数近似描述,后半段采用直线关系近似描述.

2) 船-桥碰撞简化动力学模型计算方法考虑了桥墩刚度以及上、下部结构对桥墩的约束作用等因素.

3) 当桥-船相对刚度之比小于50时,峰值撞击力随桥-船相对刚度的增大呈对数形式增大;当桥-船相对刚度之比大于等于50时,船-桥碰撞可近似看成是船舶撞击刚性体的过程,峰值撞击力可近似按欧洲统一规范取值.

4) 船-桥碰撞接触时间tc与船舶质量及船艏刚度相关,拟合出tc的经验公式,进而初步修正了我国《公路桥涵设计通用规范》中漂浮物撞击力经验公式.

5) 提出了大型桥梁复合材料防撞系统的设计理念,设计了空间格构腹板增强泡沫夹芯复合材料防撞系统.试验研究表明,复合材料防撞试件能有效延长撞击接触时间,大幅削减撞击力,适合用于桥梁防船撞领域.

6) 工程实践证明,复合材料防船撞系统可根据桥墩结构、通航状况等灵活设计成固定式、自浮式结构,具有缓冲性能好、耐腐蚀、免维护、安装更换方便等特点,能有效地降低船-桥撞击力,减轻船舶受损程度,具有较高的技术经济优势.

)

[1] Consolazio G R, Cook R A, McVay M C, et al. Barge impact testing of the St. George Island Causeway Bridge.Phase Ⅲ: physical testing and data interpretation [R]. Gainesville, FL, USA: University of Florida, 2006.

[2] Zhang B B. Influence of pier nonlinear impact angle and column shape on pier response to barge impact loading [D]. Gainesville, FL, USA: University of Florida, 2004.

[3] 罗旗帜, 何云勇, 徐中山. 连续刚构桥船桥碰撞的计算模型和动力响应[J]. 重庆交通大学学报: 自然科学版, 2010, 29(4): 501-505.

Luo Qizhi, He Yunyong, Xu Zhongshan. Calculation model and dynamic response of continuous rigid frame bridge in collision with ship [J].JournalofChongqingJiaotongUniversity:NaturalScience, 2010,29(4): 501-505. (in Chinese)

[4] 徐春林. 船舶撞击桥梁的理论分析与试验研究[D]. 南京: 南京航空航天大学航空宇航学院, 2011.

[5] Consolazio G R, Davidson M T, Cowan D R. Barge bow force-deformation relationships for barge-bridge collision analysis [J].JournaloftheTransportationResearchBoard, 2009,2131: 3-14.

[6] 王君杰, 陈诚, 汪宏, 等. 基于碰撞数值模拟的桥梁等效静力船撞力——基本公式[J]. 公路交通技术, 2009 (2): 66-70.

Wang Junjie, Chen Cheng, Wang Hong, et al. Equivalent static force of ship impact to bridge based on impact numeric simulation—fundamental formula [J].TechnologyofHighwayandTransport, 2009 (2): 66-70. (in Chinese)

[7] 陈明栋, 陈明, 陈国虞, 等. 安庆长江铁路大桥防船撞研究[J]. 重庆交通大学学报: 自然科学版, 2009, 28(2): 203-207.

Chen Mingdong, Chen Ming, Chen Guoyu, et al. Study on anti-ship collision for Anqing Yangtze River railway bridge [J].JournalofChongqingJiaotongUniversity:NaturalScience, 2009,28(2): 203-207. (in Chinese)

[8] 肖波, 李军. 船桥碰撞中桥墩防撞装置性能研究[J]. 水运工程, 2010(3): 17-20.

Xiao Bo, Li Jun. Study on pier protective device under collision of ship and bridge [J].Port&WaterwayEngineering, 2010(3): 17-20. (in Chinese)

[9] 项海帆, 范立础, 王君杰. 船撞桥设计理论的现状与需要进一步研究的问题[J]. 同济大学学报:自然科学版, 2002,30(4): 386-392.

Xiang Haifan, Fan Lichu, Wang Junjie. State of art of ship collision design for bridges and future research [J].JournalofTongjiUniversity:NaturalScience, 2002,30(4): 386-392. (in Chinese)

[10] Vrouwenvelder A C. Design for ship impact according to Eurocode Ⅰ, ship collision analysis [S]. London:CRC Press,1998.

[11] 中华人民共和国交通部. JTG D60—2004公路桥涵设计通用规范[S]. 北京: 人民交通出版社, 2004.

[12] Woisin G. Design against collision [J].Schiff&Hafen, 1979, 31 (2): 1059-1069.

[13] 岩井聪, 庄司邦昭. 关于船舶对桥梁的安全措施[J]. 中国航海, 1986(12): 153-164.

Akira Iwai, Kuniaki Shoji. On the safety measures between ship and bridge [J].NavigationofChina, 1986(12): 153-164. (in Chinese)

[14] 万志敏, 赵桂范, 杜星文. 复合材料结构的能量吸收[J]. 材料科学与工艺, 2001, 9(3): 247-249.

Wan Zhimin, Zhao Guifan, Du Xingwen. Energy absorption in structures of composite materials [J].MaterialsScience&Technology, 2001,9(3): 247-249. (in Chinese)

[15] Srivastava V K. Impact behaviour of sandwich GFRP-foam-GFRP composites [J].InternationalJournalofCompositeMaterials, 2012,2(4):63-66.

[16] Yuen S C K, Nurick G N, Starke R A. The energy absorption characteristics of double-cell tubular profiles [J].LatinAmericanJournalofSolidsandStructures, 2008,5(4): 289-317.