基于TDOA的无线定位方法及其性能分析

史小红

(东南大学信息科学与工程学院,南京 210096)

无线定位系统主要通过估计目标节点到接收机的距离或者角度对目标节点进行测距,进而计算位置信息．无线测距技术可分为基于信号接收强度(RSSI)的测距技术、基于信号到达角度(AOA)的测距技术和基于信号传输时间(TOF)的测距技术等．基于信号接收强度的测距技术是根据接收到的信号强度测出目标节点到接收点的距离[1-2]．该方法简单、易用,但易受无线环境中的多径衰落、非视距阻挡等影响[3],其定位误差较大,通常会达到20%～40%,不能满足高精度定位的要求．基于信号到达角度的测距技术通过检测无线信号到达天线阵的相位差来估计发送节点的方向．这种测距技术受接收信噪比影响较小,但是受信道干扰和多径效应的影响很大[4]．

基于信号传输时间的测距技术(TOF)[5]是目前研究最广泛的测距技术,其中基于信号传输时间差的测距技术(TDOA)因相对容易实现而更受重视．TDOA技术的核心思想是测量发射节点(即目标节点)到达2个接收节点之间的时间差,再根据时间差计算距离,进而根据双曲线定位原理计算出发射节点的位置．对目标节点进行定位的误差主要来自2个方面:一是测距误差;二是根据测距值计算目标节点位置产生的误差．前者是由于无线传输过程中多个因素的影响产生的,包括发射机和接收机之间的频率偏差、无线多径效应等．后者是由于双曲线定位中的非线性引起的,这种非线性会放大定位误差．本文将主要分析频偏和多径对定位误差的影响程度,并给出降低影响的方法．

本文建立了一个考虑多径和频偏因素的TDOA定位系统模型,其中发射信号采用QPSK调制的复数扩频序列．分析了频偏、多径等因素对到达时间差测量的影响,推导了数学表达式，并给出了仿真结果．提出了减少频偏和多径对到达时间差测量影响的方法．在实际开发的系统上进行了定位实验,结果表明,在室内环境下的定位结果良好．

1 TDOA定位原理

1.1 发送信号到达2个接收机的时间差

用图1所示的结构来讨论如何计算发射信号s(t)到达2个接收点r1(t)和r2(t)之间的时间差τ(τ=τ1-τ2)．

发送节点到接收机之间的信号传输模型如图2所示．设发送节点的基带信号为复数扩频序列,表达式为x(n)=xI(n)+jxQ(n),扩频长度为L,发送节点的载波频率为ωT,采用QPSK调制,则发送的射频信号表达式为

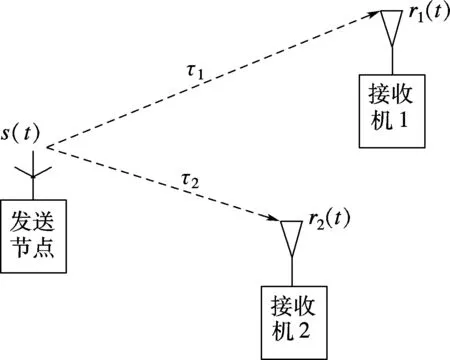
图1 发送节点到2个接收机的时间差

s(n)=x(n)ejωTn

(1)

图2 发送节点与接收机之间的信号传输模型

该信号经过的多径信道为p(n),则

(2)

式中,p(m)为第m条路径上的衰减系数．当射频信号s(n)在频率为2.4 GHz时(如Zigbee节点),其波长仅为12.5 cm．从式(2)不难看出,多径的存在可能会造成接收信号z(n)的衰落．由于信号波长很短,信号在空间衰落很频繁．当信道上有噪声v(n)(这里假定为AWGN噪声)时,则接收天线上接收到的信号为

(3)

假定接收机下变频器的本振频率为ωR,采用正交下变频得到接收的基带信号为

y(n)=r(n)e-j(ωRn+φ0)

(4)

把式(3)代入式(4),并进行推导,得

y(n)=e-jφ0[p′(n)*x(n)]ejΔωn+v′(n)

(5)

其中,p′(n)=p(n)e-jωTn,n=0,1,…,N-1;Δω=ωT-ωR;v′(n)=v(n)e-j(ωRn+φ0)．式(5)也可用图3的等效模型来描述．

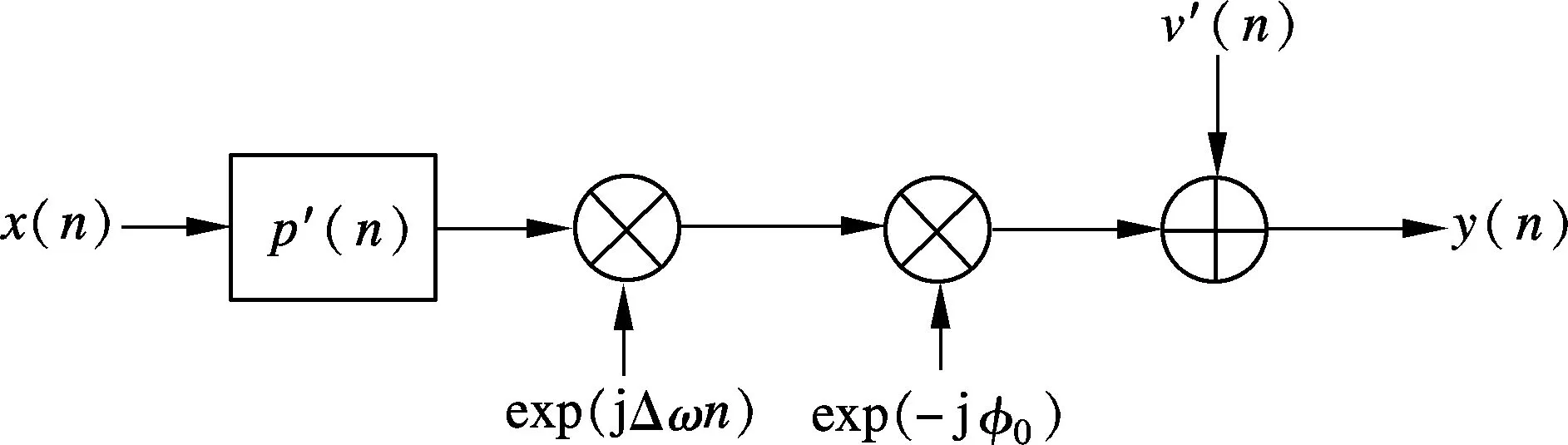
图3 无线信道中的基带信号传输等效模型

图3表明,基带信号在无线信道中传输时会受到多径p′(n)、频偏Δω、相偏φ0以及噪声v′(n)的影响．后续分析表明,这些因素可能会影响到时间差的测量精度．

在短距离无线通信中,基带信号x(n)经常采用复数扩频调制,如TI公司CC24xx系列的芯片[6],它遵循IEEE 802.15.4物理层标准．在该芯片中,将发送数据以4 bit分为一组,映射为长度L=32的扩频切普序列符号.以符号“0”为例,其对应的复数扩频序列为xI(n)={1010100100010111},xQ(n)={1101100111000010},如图4所示．

图4 IEEE 802.15.4采用的物理层复扩频信号

图4中的基带复信号x(n)经过无线信道传输后,变为式(5)描述的复信号y(n)．两者之间的时间差即信号经无线信道的传输时间,可以通过y(n)与x(n)的互相关运算获得．设y(n)=yI(n)+jyQ(n),则y(n)与x(n)的互相关值为

Rxy(n)=x(n)⊗y*(n)=[xI(n)⊗yI(n)+

xQ(n)⊗yQ(n)]+j[xQ(n)⊗yI(n)-

xI(n)⊗yQ(n)]

(6)

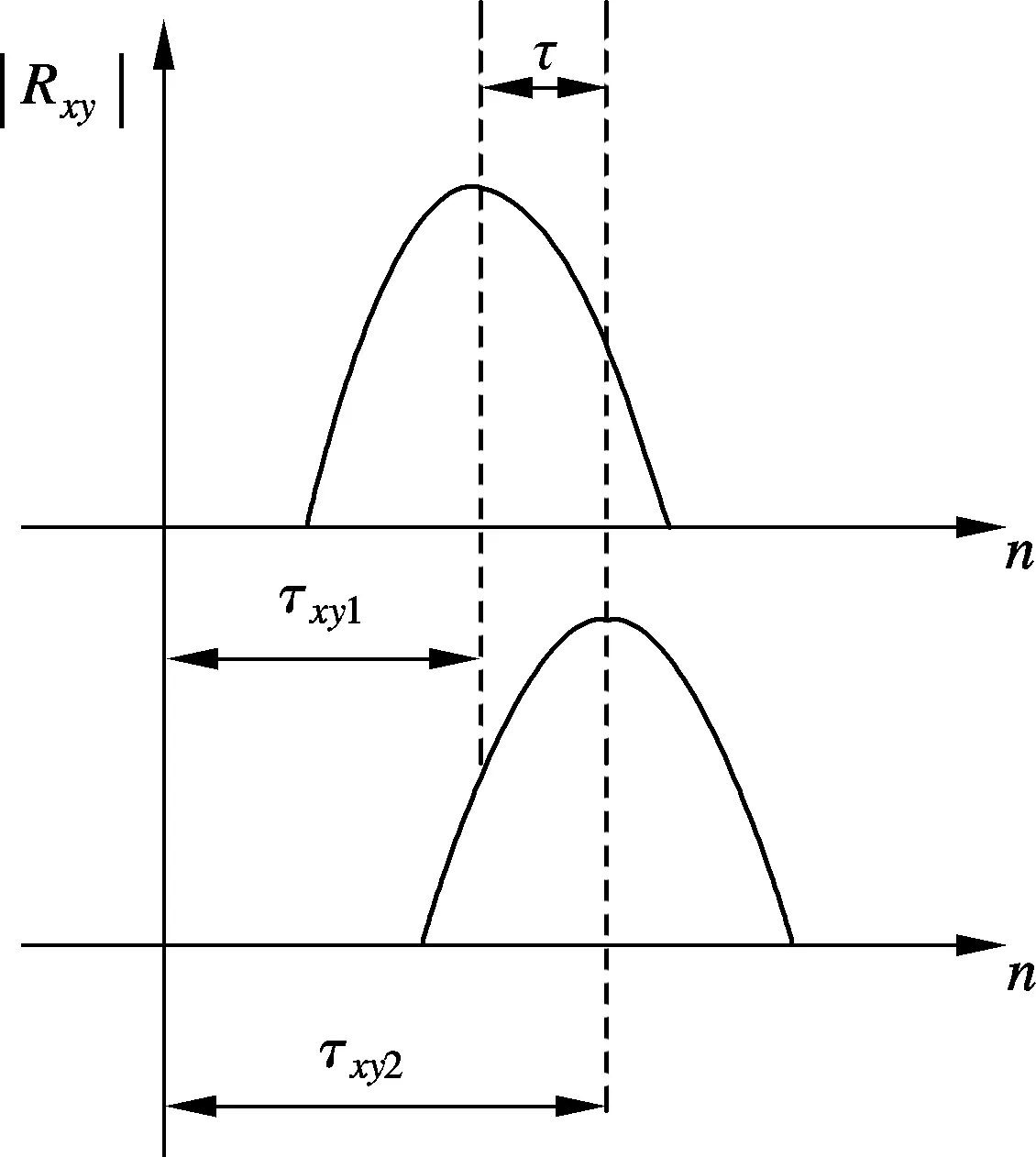
图5 2个信号的到达时间差

发送节点到2个接收机之间的距离差可由信号的到达时间差计算出来．根据TDOA原理，至少需要3个接收机(即2个时间差)才能确定出平面上一个发送节点的位置，至少需要4个接收机(即3个时间差)才能确定出立体空间中一个发送节点的位置．

1.2 基于到达时间差的发送节点位置计算

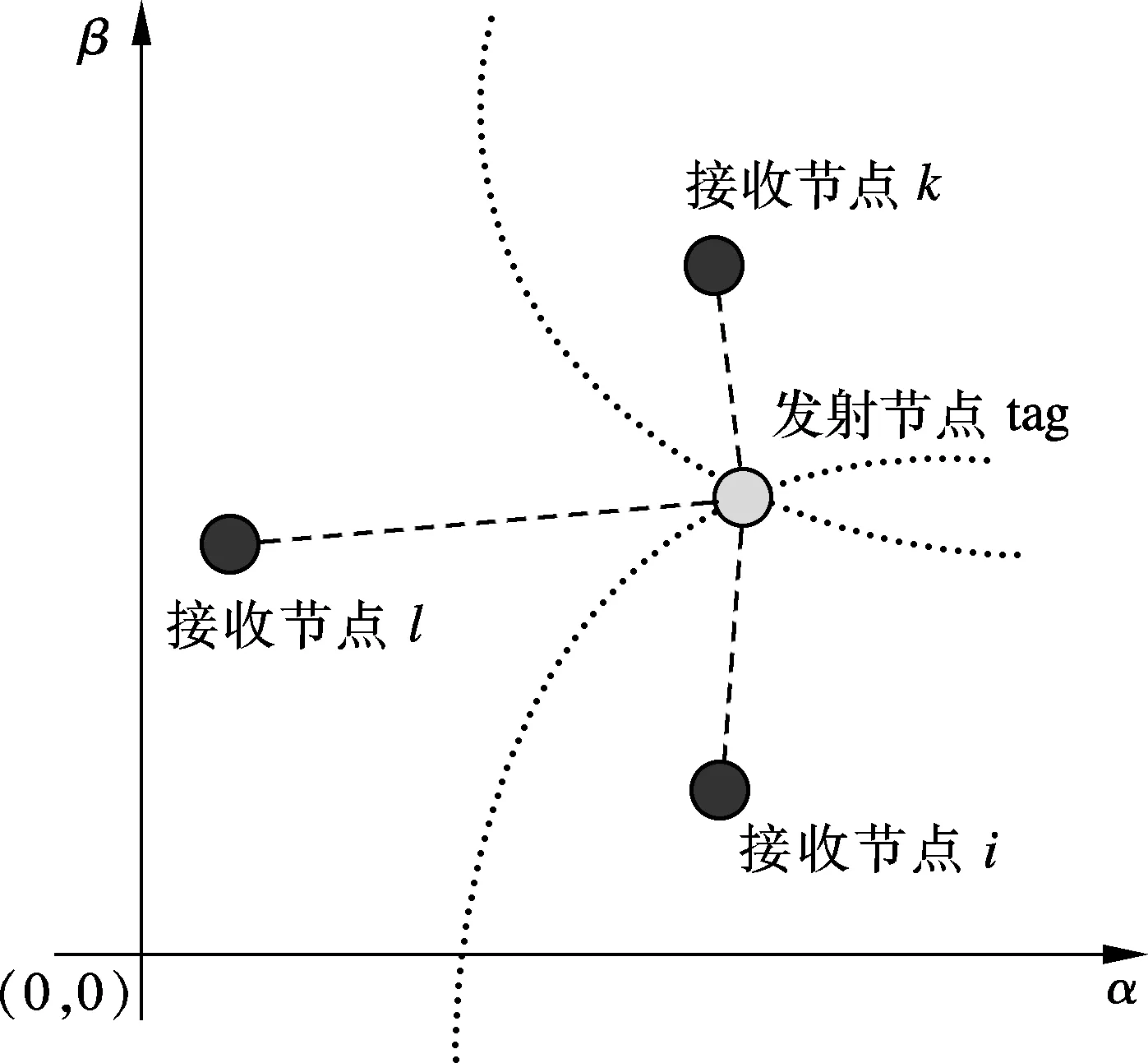
图6 基于TDOA测距技术的定位示意图

图6中,α为水平坐标,β为垂直坐标．假定接收节点i和k的位置已知,其坐标分别为(αi,βi)和(αk,βk),发送节点的位置为(μ,η),可得到目标节点到锚节点i和k的到达时间差为

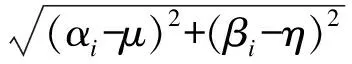
(7)

同样可得,目标节点到达节点i和l的时间差为

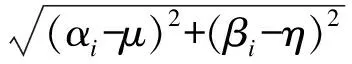
(8)

根据式(7)、(8),当测得时间差τik和τil后,即可确定节点的位置坐标(μ,η)．在定位平面中,时间差的等差线是一条双曲线,而目标节点的位置就是由2条双曲线的交点确定的．但在实际测试中,由于噪声、干扰、多径、频偏等多种因素的影响,这2条双曲线的相交关系存在3种情况:① 2条曲线交于1点;② 2条曲线交于2点;③ 2条曲线没有交点．如图7所示．图7(a)中,目标节点的位置直接由交点确定;图7(b)中,目标节点的位置由2个交点的中间点确定;而图7(c)中,目标节点的位置由2条曲线的最近点的中间点确定．

图7 2条时间差曲线的相交关系

为克服由于到达时间差测量误差引起的目标节点位置定位不准确的问题,通常采用的方法有:① 增加到达时间差测量次数,然后对时间差取平均．这种方法会减少随机因素带来的测量误差,但会增加定位时间．② 增加定位天线数,然后根据最小二乘等算法确定目标节点的位置[7-9]．这种方法有利于缩小定位误差,但过多的定位天线数意味着需要过多的接收机,这会大大增加定位系统的实现复杂度和成本．

2 频偏和多径对到达时间差的影响

参照式(6)和图5,到达时间差是通过2个接收信号与发送信号之间的互相关峰值点的时间差来获得的,因此需要分析频偏对互相关值的影响．由图5可知

τ=τxy2-τxy1=nmax[Rxy2]-nmax[Rxy1]

(9)

式中，nmax[Rxy2]表示取Rxy2最大值对应的时刻.

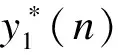
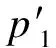
(10)

同样可得

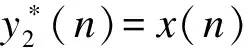
(11)

从式(11)可看出,互相关值与频偏和多径的关系很复杂,难以给出更直接的关系表达,可通过示例波形图8进行描述．这里给出了射频频率为2.4 GHz、频偏为±20 kHz的2个接收机,接收到的基带信号与发送端的基带信号按照式(10)和式(11)分别做互相关的结果．图8中,横轴为时间，即采样点数(采样率为300 MHz),纵轴为互相关值．

图8(b)中2个互相关曲线的峰值点在时间上大约偏离10个采样点,即±20 kHz的频率偏差会引起10 m的距离测量误差．

下面分析多径对到达时间差测量的影响．仍假定射频频率为2.4 GHz,接收机1收到的信号存在4条无线传输路径,接收机2收到的信号只有直达径,如表1所示．

由图9可看出,多径也会造成时间差测量的偏差．在上述条件下,误差大约为1个采样点,对应的空中距离为1 m,比频偏的影响要小．这是因为表1中假定有直达径的存在,它对互相关峰值点的贡献最大．

图8 ±20 kHz频偏对到达时间差测量的影响

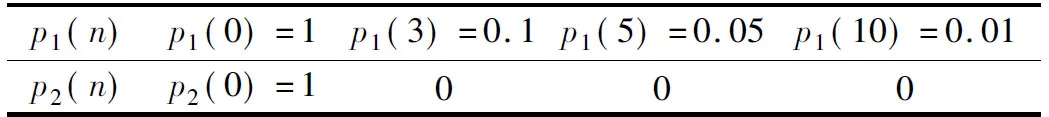
表1 接收机多径分布情况

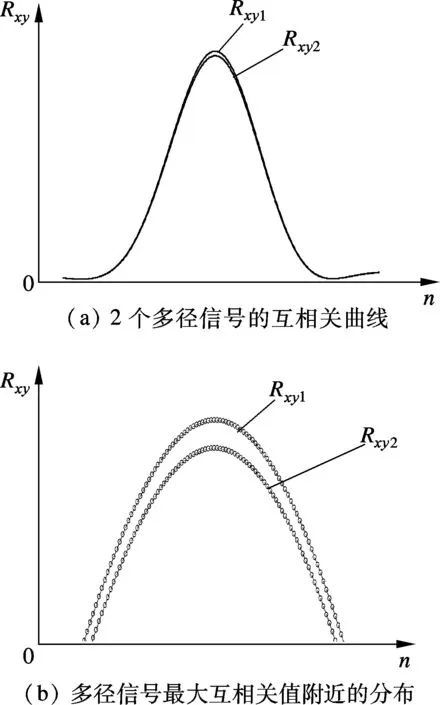
图9 4条路径对到达时间差测量的影响

3 减小频偏和多径对时间差测量影响的方法

要克服频偏对时间差测量的影响,必须估计式(10)、(11)中的e-jΔωn．这可以通过估计接收信号在一个符号内的相位变化来获得．对图5中的调制信号相位变化分析可知,在一个符号的时间宽度内,相位的总变化量为零．如果接收信号y(n)在一个符号内的总相位变化量不为零,则说明存在频偏．据此可得频偏估计方法为

(12)

由式(12)可得频偏估计值为

(13)

对后续的接收信号进行频偏校正,即

(14)

再用校正后的信号获取信号的到达时间差．

图9表明,无线传输环境的多径会对到达时间差的测量产生影响．在对接收信号校正过频偏后,频偏的影响可以忽略,即有y(n)=p(n)*x(n)．可推导得

Ryx(n)=[p(n)*x(n)]⊗x*(n)=p(n)*Rxx(n)

(15)

即多径对发送信号的作用直接反映在收发信号的互相关函数上．对式(15)进行解卷积运算即可获得对多径的估计,即

(16)

无线传输的多径现象使得接收信号可能出现衰落．在室内环境所做的测试表明,在2.4 GHz频段,由于波长很短,空中每一点的信号衰落情况都不相同,有些点会出现深衰落．这不仅导致接收信噪比很低,还会激活接收机中射频部分的自动增益控制(AGC)单元,使得信号幅度呈现快速的抖动,这些都导致不能有效定位目标．为此,接收机必须具有多天线分集接收的能力,以减少接收信号的衰落,同时正确控制接收机中信号的幅度,使其在一次定位中是稳定的．由于本文的目的是求取准确的信号到达时刻,分集接收方案必须不能与时间因素有关,否则会影响定位的精度,因此,宜采用多个独立接收机的空中分集方案,而不能采用多径合并的方案,如图10所示．

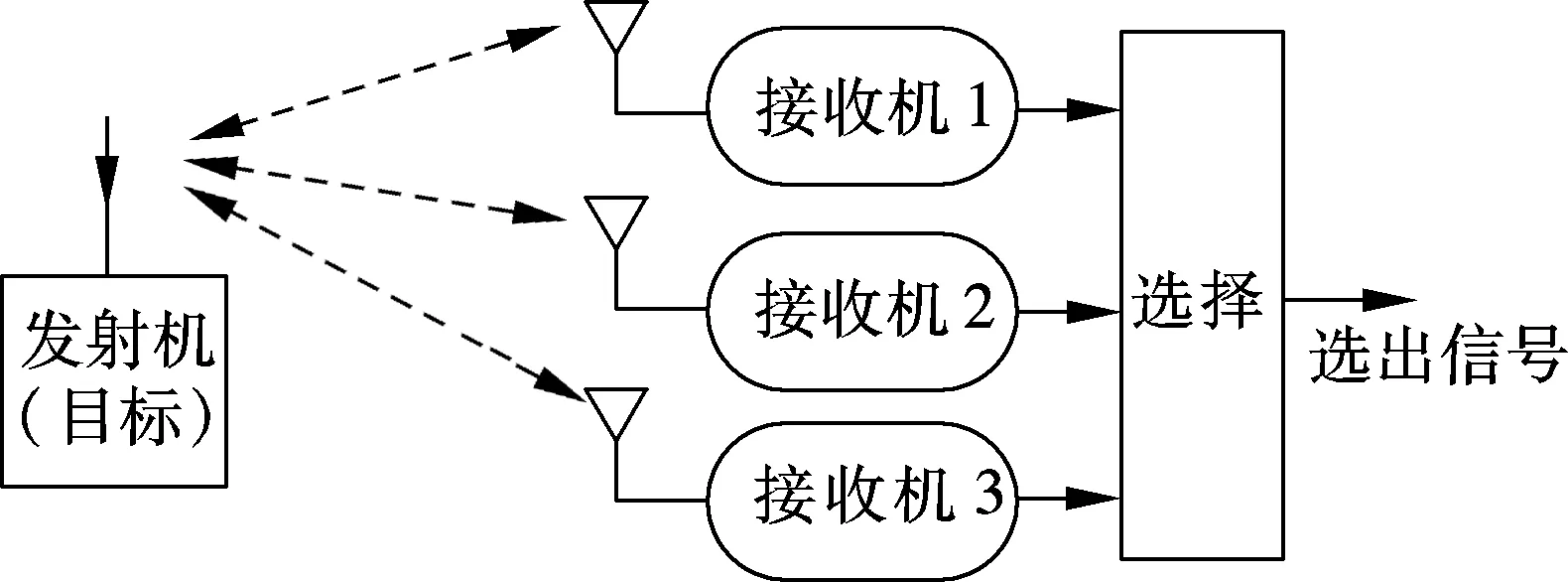
图10 采用3个独立接收机的空间分集接收机示意图

4 测试结果

为检验上述定位方法的性能,采用了图6所示的3个接收节点的定位方案．测量环境为室内办公环境,面积300 m2,有明显多径存在;目标节点采用2.4 GHz CC2530 Zigbee模块, 基带切普速率为2 Mchip/s; 在接收机中,接收信号从射频下变频到基带,然后将接收信号与本地序列进行复数相关运算;基带信号采样率为300 MHz;3个接收机的位置坐标分别为A(-0.2 m,-6.0 m),B(-6.0 m,3.3 m),C(8.5 m,0 m); 目标节点实际位置为T(0 m,-2 m)．

测得的距离差及定位误差情况如表2所示．表2中的定位位置误差为测出的目标节点的位置与其实际位置的欧氏距离偏差．A，B，C三点间的距离均约为12 m,平均偏差为0.34 m,因此采用本文方案的定位误差平均为2.8%,优于已有的基于TDOA的无线定位方法[12]．

5 结语

本文研究了基于TDOA的无线定位中影响定位精度的关键技术问题,提出了校正频偏和克服多径的方法,形成了具有实用价值的无线高精度定位方案．由于在计算多个接收机之间的时间差时需要严格的时间同步,这些接收机可部署在一部车辆上或者用电缆直接连接在一起,因此该方案可用于局部范围内对无线目标的高精度定位．后续的研究可集中在对所测量到的时间差数据的处理上,如对数据进行卡尔曼滤波,减少数据的摆幅,以及通过对同一目标的多次定位进一步提高定位精度等．

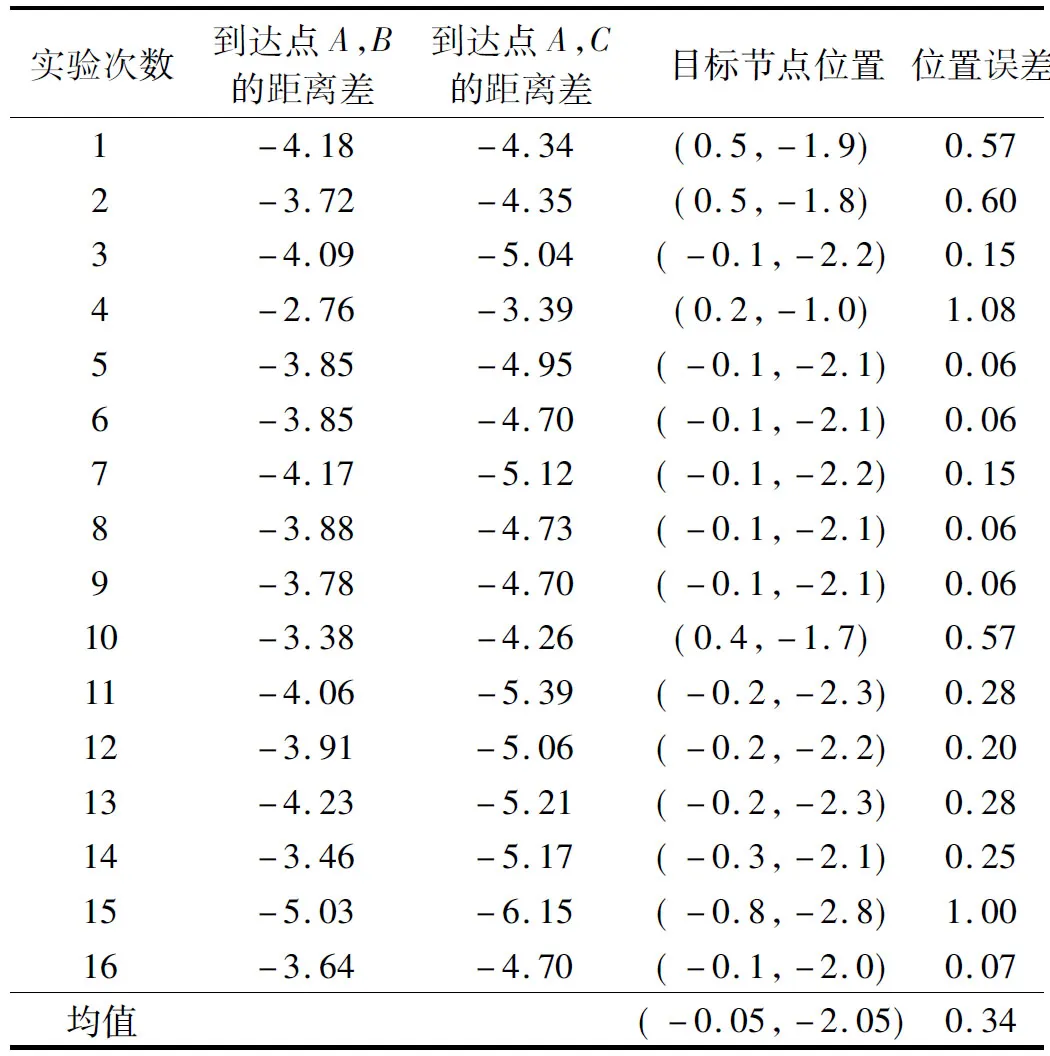
表2 测得的距离差及定位误差情况 m

)

[1]孙佩刚, 赵海. 智能空间中RSSI定位问题研究[J]. 电子学报,2007,35(7):1240-1245.

Sun Peigang, Zhao Hai. Research on RSSI positioning problem in intelligent space [J].ChineseJournalofElectronics, 2007,35(7): 1240-1245. (in Chinese)

[2]Wang W D, Zhu Q X. RSS-based Monte Carlo localisation for mobile sensor networks [J].IETCommunications, 2008,2(5): 673-681.

[3]Sha K, Shi W, Watkins O. Using wireless sensor network for rescue application:requirements and challenges [C]//ProceedingofElectro/InformationTechnology. East Lansing, MI, USA, 2006: 239-244.

[4]Rappaport T S, Reed J H, Woerner B D. Position loca-

tion using wireless communications on highways of the future [J].IEEECommunicationsMagazine, 1996,34(10): 33-41.

[5]Priyantha N B, Chakraborty A, Balakrishnan H. The cricket location-support system [C]//ProceedingsoftheSixthAnnualACMInternationalConferenceonMobileComputingandNetworking. Boston, MA, USA, 2000: 32-43.

[6]Texas Instruments Incorporate. CC2430 Datasheet (rev. 2.1) SWRS036F [EB/OL]. (2012-02-16)[2012-06-20]. http://www.ti.com/product/2430.

[7]Chan Y T, HO K C. A simple and efficient estimator for hyperbolic location [J].IEEETransactionsonSignalProcessing, 1994,42(8): 1905-1915.

[8]So H C, Hui S P. Constrained location algorithm using TDOA measurements [J].IEICETransactionsonFundamentals,CommunicationsandComputerSciences, 2003, E86-A(12): 3291-3293.

[9]Li W C, Wei P, Xiao X C. A robust TDOA-based location method and its performance analysis [J].ScienceinChinaSeriesF—InformationSciences, 2009,52(5): 876-882.

[10]厉力华,何振亚. 关于多径信号分辨及其性能界[J]. 东南大学学报:自然科学版,1992, 22(5): 14-21.

Li Lihua, He Zhenya. On multipath signal distinguishing and its performance boundary [J].JournalofSoutheastUniversity:NaturalScienceEdition, 1992,22(5): 14-21. (in Chinese)

[11]Chung W C, SHa D. An accurate ultra wideband (UWB) ranging for precision asset location [C]//ProceedingsofIEEEConferenceonUltraWidebandSystemsandTechnologies. Grenoble, France, 2003: 389-393.

[12]彭宇,王丹. 无线传感器网络定位技术综述[J].电子测量与仪器学报,2011, 25(5): 389-396.

Peng Yu, Wang Dan. Summary of wireless sensor network positioning techniques[J].JournalofElectronicMeasurementandInstruments, 2011,25(5): 389-396. (in Chinese)