风险态度对建筑工程项目投标均衡策略的影响及对策
2013-03-22成于思李启明袁竞峰
成于思 李启明 袁竞峰
(东南大学土木工程学院,南京210096)
拍卖(auction)或招标是现代经济社会中处理非对称信息下商品交易的一种普遍形式,在建筑工程招投标领域得到了广泛的应用[1-2].Holt[3]研究了基于密封拍卖模型的采购合同的委托承接过程,提出了最低价格招投标和第二最低价格招投标程序,以及相应的均衡策略.由于在该模型中将投标人建模为风险中性及对称,与现实中的条件有所偏差,因此研究人员对此基本模型进行了拓展.Maskin等[4]研究了投标人价值分布为非对称模型下的均衡存在条件以及均衡策略的表达式.在此基础上,Bajari[5]给出了非对称模型下均衡策略的数值解法.Cox等[6]将模型的风险中性假设推广到不同风险态度条件,给出了均衡策略.在此基础上,Boening等[7]用数值方法对Cox模型中较难给出理论解的部分进行仿真.Chen等[8]用实验经济学的方法研究了不同风险态度的一阶拍卖模型.然而Cox模型是应用于最高价格物品拍卖模型,与工程招投标模型不同.李建章[9]对比分析了风险参数相同的投标人和不相同的投标人的博弈行为,以及参数对均衡策略的影响.
在实际的工程招投标过程中,经常存在低价中标现象[10],使得基本的理论模型与实际相比产生了偏差.同时,在建设工程招投标中,价格只是衡量投标方案的标准之一,业主往往还需要考虑其他非价格属性(如质量、完工日期、项目经理等).Che[11]提出了二维多属性拍卖模型,而David等[12]将之推广到多维属性拍卖中.孙亚辉等[13]改进了David模型中的效用函数,使之更适合实际情况.在建设工程招投标中引入多维标准,解决低价中标问题是本文的研究目的.
本文首先在密封价格拍卖模型的基础上考虑了风险态度因素,对低价中标现象进行了理论分析.其次,引入多属性招标模型,分析模型中的均衡策略,进而解决低价中标问题,实现工程的整体性能优化.最后通过实例给出了投标及评分过程.
1 建设工程招投标基本模型
根据最低价格密封拍卖模型,基本的招投标过程如下:业主(即招标人)有一项建设工程要发包,根据招投标法规定,采用最低价格密封招标.承包商(即投标人)将自己对工程的报价写下来装入信封中,密封后交给招标单位,招标人开标,选择报价最低方作为工程承包者.
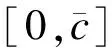
假定投标人i的出价bi(ci)是其成本ci的严格递增可微函数[14].由于博弈是对称的,只需要考虑对称的均衡报价策略:b=b*(c).给定c和b,投标人的期望收益为
投标人i面临的问题是
解此最优化问题,得到
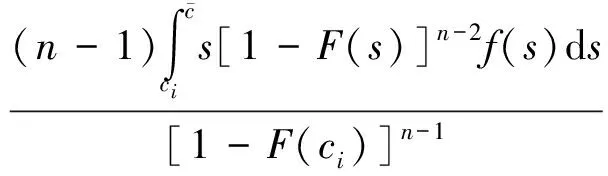
具体推导过程见文献[3].当投标人数增加时,投标方报价将接近成本.招标方采用这种博弈机制使得投标方揭示各自的私人成本信息.
尽管基本的投标拍卖模型可以优化招投标各方的收益,然而其基本的假设,即所有的投标者都是风险中性的,与现实中工程投标者的风险态度不符,因此限制了模型的应用.面对同一个招标工程,投标者采取的投标策略分为保守型和中立型[6].产生不同投标策略的原因主要有:① 工程招标与一般的商品采购招标不同,具有工期长、建造环境复杂、不可预见因素较多等特征.不同的承包商对于这些风险因素做出不同的判断,既可能认为会增加成本,也可能认为会减少成本.此时,承包商会选择不同的投标策略.② 由于工程合同存在一定模糊性和不完整性,部分承包商采取事前低价中标的策略,中标之后再以合同变更为借口提高价款,或降低工程质量进而弥补低价可能造成的损失.下面将修改基本模型,加入承包商风险态度变量,研究其对均衡投标函数的影响.
2 考虑风险态度的招标报价模型
改变招投标基本模型中投标人风险中性的设定,将每个投标人的效用函数建模为简单幂函数:Ui(yi)=(yi)ri,其中yi表示收入,ri为风险参数[6].当0≤ri<1时,投标人i为风险回避型投标人;当ri=1时,投标人为风险中性.ri为一随机变量,具有相同的概率分布函数,记为Φ,支持度表示为[0,rmax],其中rmax≤1.每个投标人知道自己的风险参数值,但仅知其他投标人的风险参数的分布函数Φ.

(1)
ci可以看作报价函数的反函数,可表示为
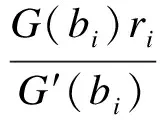
(2)
因为bi是ci的增函数,所以h(bi,ri)随着bi递增.由式(2)可知,风险参数为rmax的投标人报的最低价为
(3)
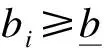

(4)
投标人以报价b赢得合同的概率G(b)为
G(b)=Fn-1(b)=I(F(b))
(5)
将式(5)代入式(4),可得

(6)
经过移项整理后,得到
(7)
令θ=1/E(r),式(7)两边同时乘以积分系数I(F)θ,可得

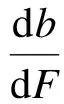
(8)

(9)
对式(9)进行积分,有
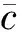
(10)

(11)
将式(5)代入式(2),有
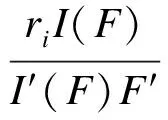
(12)
对式(11)两边求导,将得到的I′(F)F′的表达式代入式(12),可得到
(13)
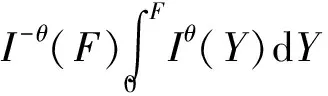

(14)
此时均衡报价函数被式(14)与式(13)定义.将式(5)代入式(13)中,得到

(15)
将式(14)代入式(15)中,得到如下均衡报价策略:
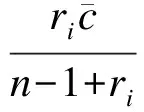
(16)
下面讨论ri对ci的影响.假设任意2个承包商满足c1=c2=c,r1 从上述推导可看出,投标人风险态度的不同使得成本较高者可能中标,此时业主并未选到最优投标商.而承包商以低价中标之后,为了弥补利润,中标者很可能采取在工程建设过程中偷工减料、降低施工质量、改变施工方案等措施,这些都将损害业主利益[10].为了解决这一问题,考虑在拍卖过程中不再以价格为唯一标准,加入质量标准、施工方案评价标准、施工方人员技术标准等,同时应将这些条款加入合同中,保证这些标准的执行力.在面对较为严谨细致的合同时,承包商需要考虑在施工过程中违反合同所要付出的代价,这在一定程度上会改变承包商在投标报价时的风险态度,使承包商更偏向于风险中性. 下面将多属性因素加入基本招投标模型,分析均衡报价策略的改变.业主在发布的招标文件中规定影响投标结果的(m+1)个属性及其权重,其中价格属性为b,非价格属性表示为qj(j=1,2,…,m).qj越大表示对投标人的要求越高,投标人在该属性上的成本越高.投标人在中标下的效用函数表示为 bi-fc(ci,qi1,…,qim) 式中,ci为投标方的成本参数,服从概率分布F(ci);aj表示第j个属性的成本系数,在此假设各个投标人同一属性下的成本系数相同.招标人的效用函数表示为 -b+fs(qi1,…,qim) (17) 式中,wj为第j个属性的权重.招标人公布评分函数,用以挑选承包商.文献[12]提出招标人的评分准则的权重可以与式(17)中的效用函数wj不同,进而优化招标人效用.而在建设工程招标中,需要遵循公开公平公正原则,因此评分函数S(b,q1,…,qm)与式(17)相同. David等[12]证明给定多属性招投标评分规则和投标方效用函数时,使得投标方效用最大化的非价格属性的选择独立于价格属性,且最优价格属性值为 (18) 最优化的一阶条件满足式(18)右边部分对qij求导等于零,由此得到 (19) 投标人的均衡报价函数是如下最优化问题的解: (20) 将p(·)认为是v的满足单调性和对称性的报价函数,利用一阶密封价格拍卖模型中的方法可求得式(20)的解为 (21) 假设某业主需要修建一栋大楼,采用公开招标的方式选择施工方.在招标的评分办法中,除价格之外提出几个标准:① 质量标准q1,包括承诺质量等级、违约经济处罚、质量保障体系等分项;② 施工方人员素质标准q2,包括项目经理资历、施工人员资历以及培训等分项;③ 施工方案性能标准q3,包括工期进度计划科学性、施工方案可行性、施工技术先进性等分项.每项标准的成本参数和成本系数与各个分项有关.这里各属性取值与成本参数和成本系数一起决定了施工方效用中的成本,这与实际中专家给出的各属性评分不同,两者之间是递增函数关系.假设各施工方成本参数在[0,1]上独立且服从均匀分布函数.各参与方的效用函数如下: 承包商根据评分规则进行投标,评分函数为 利用式(19)、(21),求得3个承包商的报价如下: BID1=(p=5.738,q1=4,q2=4,q3=6.25) BID2=(p=3.415,q1=1.78,q2=1.78,q3=2.78) BID3=(p=2.688,q1=1.23,q2=1.23,q3=1.93) 承包商的得分分别为:S1=3.61,S2=2.82,S3=2.50.由结果可知提供高质量高性能方案的承包商的投标价也相应提高.承包商1的得分最高,将赢得合同. 从本例中也可以看出并非价格最低的承包商获得合同,而是综合考虑了价格标准和非价格标准进行评选.这样一方面可以减轻承包商低价中标策略给业主造成的损失,保障了业主在整个工程上的长远利益;另一方面也促进承包商在工程开始之前做好充分调研准备,减少盲目投标带来的损失. 本文研究了建筑工程项目招投标过程中的博弈行为,将基本的密封拍卖模型中风险中性的假设条件拓展到不同风险参数条件,使之更适合实际招投标过程.通过分析不同风险参数下的均衡报价策略,可以看出,现实中投标人的风险态度使得最低价格密封拍卖不一定是帕累托有效.为了解决低价中标现象,使用多属性招投标模式挑选承包商,当合同不确定性降低时,承包商风险态度偏向中性.通过算例可以看出当承包商提供高质量的工程时,尽管报价最高也能赢得工程.本文中的招投标建模针对不可分的单一对象考虑多属性标准,而建设工程的招投标往往是将一个工程分解为多个对象分别报价.未来的工作将研究多对象多属性结合的招投标模型中的最优投标策略问题. ) [1]Mohamed K A, Khoury S S, Hafez S M. Contractor’s decision for bid profit reduction within opportunistic bidding behavior of claims recovery[J].InternationalJournalofProjectManagement, 2011,29(1): 93-107. [2]Oo B L, Drew D S, Lo H P. A comparison of contractors’ decision to bid behavior according to different market environments[J].InternationalJournalofProjectManagement, 2008,26(4): 439-447. [3]Holt C A. Competitive bidding for contracts under alternative auction procedures[J].JournalofPoliticalEconomy, 1980,88(3): 433-445. [4]Maskin E, Riley J. Asymmetric auctions[J].TheReviewofEconomicStudies, 2000,67(3): 413-438. [5]Bajari P. Comparing competition and collusion: a numerical approach[J].EconomicTheory, 2001,18(1): 187-205. [6]Cox J C, Smith V L, Walker J M. Theory and individual behavior in first-price auctions[J].JournalofRiskandUncertainty, 1988,1(1): 61-69. [7]Boening M V, Rassenti S J, Smith V. Numerical computation of equilibrium bid functions in a first-price auction with heterogeneous risk attitude[J].ExperimentalEconomics, 1998,1(2): 147-159. [8]Chen Y, Katuscak P, Ozdenoren E. Sealed bid auctions with ambiguity: theory and experiments[J].JournalofEconomicTheory, 2007,136(1): 513-535. [9]李建章. 风险态度与密封招标中的均衡投标策略[J]. 重庆交通学院学报, 2006, 25(1): 120-124. Li Jianzhang. The equilibrium bidding strategy for the bidders with different attitudes toward risk in the first price sealed auctions[J].JournalofChongqingJiaotongInstitute, 2006,25(1): 120-124.(in Chinese) [10]王维国, 刘德海. 建筑工程项目招标低价中标现象的不完全信息博弈理论分析[J]. 中国管理科学, 2008, 10(16): 444-449. Wang Weiguo, Liu Dehai. The incomplete information game-theoretical analysis of winning the bid with low-priced in engineering project[J].ChineseJournalofManagementScience, 2008,10(16): 444-449.(in Chinese) [11]Che Y K. Design competition through multidimensional auctions[J].JournalofEconomics, 1993,24(3): 668-680. [12]David E, Azoulay-Schwartz R, Kraus S. Bidding in sealed-bid and English multi-attribute auctions[J].DecisionSupportSystems, 2006,42(2): 527-556. [13]孙亚辉, 冯玉强. 多属性密封拍卖模型及最优投标策略[J]. 系统工程理论与实践, 2010, 7(7): 1185-1189. Sun Yahui, Feng Yuqiang. Multi-attribute sealed-bid auction model and optimal bidding strategies[J].SystemsEngineering—Theory&Practice, 2010,7(7): 1185-1189.(in Chinese) [14]张维迎. 博弈论与信息经济学[M]. 上海:格致出版社, 2004:152-153.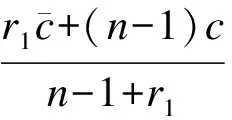

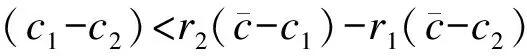
3 改进的建设工程招投标模型
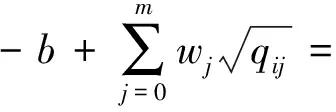
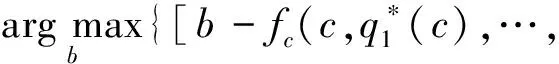

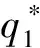

4 案例分析
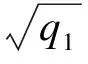



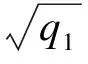
5 结语
