维修时间受限的单部件系统几何过程维修模型
2013-03-22王冠军张元林
王冠军 张元林
(东南大学数学系,南京 210096)
可靠性系统发生故障时,通过维修可以恢复其工作状态.通常情况下,逐次维修后系统的性能会逐渐下降,最终老化不能使用.同样由于系统老化,维修变得困难,维修时间越来越长.Lam[1-2]使用几何过程维修模型来描述可靠性系统状态随故障次数增加逐渐衰减这一现象,并提出了故障次数N和总工作时间T两种更换策略.Zhang[3]推广了几何过程模型,研究了二元更换策略(T,N).近10年来,几何过程维修的研究取得了很大进展,如文献[4-5]研究了系统在外部冲击下的几何过程维修模型,文献[6-7]分别研究了几何过程维修下的贮备系统的预防维修问题和多状态系统的最优维修更换策略问题,文献[8]讨论了具有2种故障的系统的最优更换问题.文献[9]则对几何过程近20年的研究和发展做了全面的介绍.
系统故障后,由于时间、经济等原因不能一直修下去,所以需要对维修时间进行限制,超出这个时间时放弃维修,系统被更换.维修时间受限的维修模型较早由Nakagawa和Osaki[10]提出.Wang[11]对维修时间受限问题研究进行了综述,介绍了退化系统下基于维修时间受限的几个维修更换模型.Dohi 等[12]研究了不完全维修下的最优维修时间受限阈值,并应用Lorenz变换给出了阈值的非参数估计.
本文提出了维修时间受限下的几何过程维修模型.逐次维修时间随机递增,构成几何过程.当维修时间超出给定阈值时放弃维修,系统被更换.系统维修次数达到N时不再维修,下一次发生故障时系统被更换.在这些假设下,研究了系统的一些可靠性指标和维修更换策略问题.利用一个数值例子对理论结果进行了模拟,并分析了维修时间阈值对最优策略的影响.
1 几何过程的定义
下面给出几何过程的定义:
定义1设{Xn,n≥1}是一个独立的非负随机变量序列,如果Xn的分布函数为Fn(t)=F(an-1t),n=1,2,…,其中a>0为常数,F(t)为一分布函数,则称{Xn,n≥1}为一个几何过程,常数a称为几何过程的比率.
显然,如果a>1,则几何过程{Xn,n≥1}随机递减;如果0 单部件系统中包含一个维修工,系统发生故障时,由维修工对其进行维修.对模型作如下假设: 1) 系统逐次维修后工作时间序列{Xn,n≥1}随机递减,构成递减的几何过程.记X1的分布函数为F(x),Xn的分布函数为Fn(x)=F(an-1x), 其中a>1,n=1,2,….数学期望E[X1]=λ,λ>0为常数. 2) 首次维修时间Y1服从指数分布e(1/μ),μ>0为常数.逐次维修时间序列{Yn,n≥1}构成递增几何过程,即第n次维修时间Yn服从指数分布e(bn-1/μ),其中0 3) 维修时间的上限阈值为θ,θ>0为常数.若维修时间达到θ还未修好,则不再继续维修,更换新系统. 4) 工作时间序列{Xn,n≥1}和维修时间序列{Yn,n≥1}是相互独立的. 5) 系统维修N次之后不再维修,在发生第N+1次故障时被更换. 6) 系统的更换费用为CR,系统的维修费用CM(Y)是维修时间Y的线性函数,即CM(Y)=C0+C1Y,其中,C0为基本维修费用,C1为与时间有关的费用率. 本节对系统运行中的一些变量进行分析,并给出一些数量指标. 系统首次更换的时间记为τ1,第n次更换的时间记为τn,则更新时间序列{τn,n≥1}生成一个更新过程,τn-τn-1为更新过程的一个更新周期.在上述假设下,一个更新周期中系统的总工作时间可表示为 U(θ,N)=X1+X2I{Y1<θ}+ X3I{Y1<θ,Y2<θ}+…+ XN+1I{Y1<θ,…,YN<θ} (1) 式中,I{·}为示性函数.则一个更新周期中的平均工作时间为 E[U(θ,N)]=E[X1]+E[X2I{Y1<θ}]+…+ E[XN+1I{Y1<θ,…,YN<θ}]= (2) 在一个更新周期中,系统的总维修时间可表示为 V(θ,N)=η1+η2I{Y1<θ}+ η3I{Y1<θ,Y2<θ}+…+ ηNI{Y1<θ,…,YN-1<θ} (3) 其中,ηk=min{Yk,θ}.ηk的数学期望经计算可得 (4) 于是平均维修时间为 E[V(θ,N)]=E[η1]+E[η2I{Y1<θ}]+…+ E[ηNI{Y1<θ,…,YN-1<θ}]= (5) 用ξ(θ,N)表示一个更新周期中的维修次数,则有 p(ξ(θ,N)≥1)=1 p(ξ(θ,N)≥k)=P(Y1<θ,Y2<θ,…, Yk-1<θ)=G(θ)…G(bk-2θ)= (6) 进一步可以求得一个更新周期内的平均维修次数为 (7) 由交替更新定理可得系统长期运行平均可用度为 (8) 系统在一个更换周期中的故障次数记为δ(θ,N),显然有δ(θ,N)=ξ(θ,N)+1.于是系统长期运行单位工作时间平均故障频度为 (9) 当θ→+∞时,极限平均可用度和极限平均故障频度分别为 (10) (11) 系统在一个更新周期中总的费用为 w(θ,N)=(C0+C1η1)+(C0+ C1η2)I{Y1<θ}+…+(C0+ C1ηN)I{Y1<θ,…,YN-1<θ}+CR (12) 一个更新周期中的维修次数ξ(θ,N)还可表示为 ξ(θ,N)=1+I{Y1<θ}+ I{Y1<θ,Y2<θ}+…+ I{Y1<θ,…,YN-1<θ} (13) 因此,费用W(θ,N)的表达式为 w(θ,N)=C0ξ(θ,N)+C1V(θ,N)+CR (14) 于是一个更新周期中总平均费用为 E[W(θ,N)]=C0E[ξ(θ,N)]+C1E[V(θ,N)]+CR= (15) 由更新报酬定理[13]可得系统长期运行平均费用率为 (16) 当θ→+∞时可得 (17) 这正是文献[1]中策略N下系统平均费用率的表达式. 假定模型参数的取值分别为:λ=50,μ=10,a=1.05,b=0.9,θ=40,C0=30,C1=5,CR=500. 将上述参数值代入式(7)、(8)、(12),可算出在策略N下系统长期运行平均费用率函数C(θ,N)、平均可用度A(θ,N)和平均维修次数ξ(θ,N)的数值结果,如表1所示.可以看出,当N=9时系统平均费用率达到最小值2.856 6,所以N*=9是以平均运行费用率为优化目标时的最优更换策略.此时,系统平均可用度为0.763 4,一个更换周期中平均维修次数为7.445 0.从表1还可看出,随着更换策略N的增加,平均可用度A(θ,N)逐渐降低,平均维修数ξ(θ,N)逐渐增大. 表1 平均费用率函数、平均可用度和平均维修次数的数值结果 图1和图2分别给出了系统平均运行费用率和平均可用度关于更换策略N的曲线.这2条曲线与表1中的数值是相对应的.从图1和图2中也可看出,当N较大时 (如N>20), 平均费用率函数C(θ,N)和平均可用度A(θ,N)几乎不再变化,这是由于在给定参数和维修时间限制下,当N很大时,系统很少是按计划更换的,多数情况下系统是由于维修时间限制策略产生更换.本文对不同的N也计算了一个更换周期中的平均维修数ξ(θ,N),当N很大时,ξ(θ,N)变化甚微,这也表明更换行为由维修时间限制策略所主导. 图1 平均费用率函数C(θ,N)关于N的曲线(θ=40) 图2 平均可用度A(θ,N)关于N的曲线(θ=40) 表2给出了维修时间限制θ变化时系统的最优更换策略和相应的平均费用率.从数值结果可看出,随着阈值θ的减小,最优策略N*的值逐渐增大.这是因为当阈值变小时,根据给定维修策略系统更容易被更换掉,作为一种补偿,当维修时间不超过阈值时,尽量多修几次以平衡严苛的更换规则. 表2 不同维修时间阈值下的最优更换策略和平均费用率 本文研究了一个维修时间受限的单部件系统的维修更换问题,系统工作时间和维修时间分布分别服从递减和递增的几何过程.对于给定的维修时间上限阈值,当系统维修时间大于阈值时,停止维修并且更换新系统.通过模型分析,不仅给出了一些重要的可靠性指标,如系统平均可用度、平均故障频度等,并且基于平均费用率函数研究了系统的最优维修更换策略.数值模拟表明在给定参数范围内存在唯一最优策略.此外,随着维修时间阈值的增大,最优更换策略N*有减小的趋势. ) [1] Lam Y. Geometric processes and replacement problem [J].ActaMathematicaApplicandaeSinica, 1988,4(4): 366-377. [2] Lam Y. A note on the optimal replacement problem [J].AdvancesinAppliedProbability, 1988,20(2): 479-482. [3] Zhang Yuanlin. A bivariate optimal replacement policy for a repairable system [J].JournalofAppliedProbability, 1994,31(4):1123-1127. [4] 王冠军,张元林.δ_冲击模型及其最优更换策略[J]. 东南大学学报:自然科学版,2001,31(5):121-124. Wang Guanjun, Zhang Yuanlin.δ_shock model and the optimal replacement policy [J].JournalofSoutheastUniversity:NaturalScienceEdition, 2001,31(5):121-124. (in Chinese) [5] 王冠军,张元林. 一般δ_冲击模型及其最优更换策略[J]. 运筹学学报, 2003, 7(3):75-82. Wang Guanjun, Zhang Yuanlin. Generalδ_shock model and its optimal replacement policy [J].ORTransactions,2003,7(3):75-82. (in Chinese) [6] Wang Guanjun, Zhang Yuanlin. A bivariate optimal replacement policy for a cold standby repairable system with preventive repair [J].AppliedMathematicsandComputation, 2011,218(7):3158-3165. [7] Zhang Yuanlin, Wang Guanjun. An extended replacement policy for a deteriorating system with multi-failure modes [J].AppliedMathematicsandComputation, 2011,218(5): 1820-1830. [8] Wang Guanjun, Zhang Yuanlin. Optimal repair-replacement policies for a system with two types of failures [J].EuropeanJournalofOperationalResearch, 2013,226(3): 500-506. [9] Lam Y.Thegeometricprocessanditsapplications[M]. Singapore: World Scientific, 2007: 37-40. [10] Nakagawa T, Osaki S. The optimum repair limit replacement policies [J].OperationalResearchQuarterly, 1974,25(2): 311-317. [11] Wang H. A survey of maintenance policies of deteriorating systems [J].EuropeanJournalofOperationalResearch, 2002,139(3):249-489. [12] Dohi T, Ashioka A. Replacement policy with imperfect repair: Lorenz transform approach [J].MathematicalandComputerModelling, 2003,38(11): 1169-1176. [13] Ross S M.Stochasticprocesses[M]. New York: Wiley, 1996:132-140.2 模型假设
3 模型分析





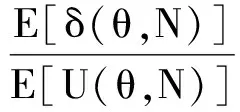

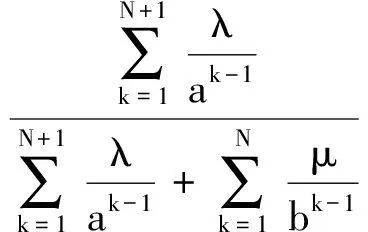
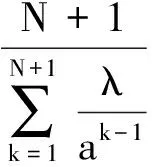

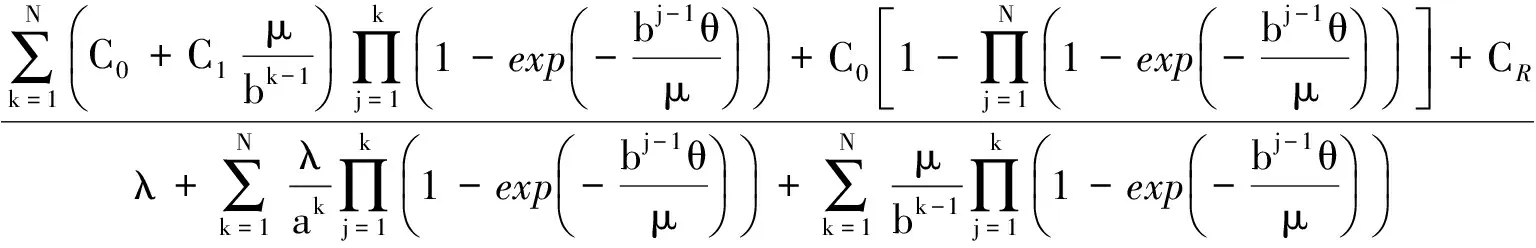
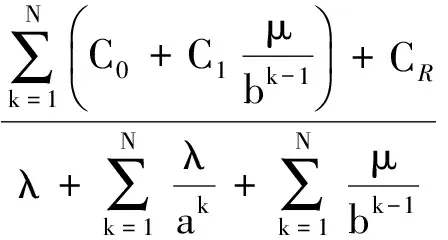
4 数值例子




5 结语
