基于视差区域分割的动态规划立体匹配算法改进
2013-03-21王敬东李秀馨许丽红
王敬东, 陈 思, 李秀馨, 许丽红
(南京航空航天大学自动化学院,江苏 南京 210016)
机器人在未知环境中运动时须准确、快速地辨别障碍物的位置,寻找出可行走的道路区域,这就要求应用于视觉导航系统中的立体视觉匹配算法具有较高的准确性和实时性。目前,一些立体匹配算法在精度方面取得了一定提高,但计算量与处理时间都显著增加。在全局算法中,DP(Dynamic Programming动态规划)方法计算速度较快,能够在较低的硬件条件下满足实时性需求,然而其匹配精度不高。
Geiger[1]等最早提出基于像素对亮度差异的DP立体匹配算法,但该算法缺少完善的全局约束项,易出现条纹瑕疵,匹配精度较低;Gong[2]等介绍了一种基于可靠性DP算法,该算法利用了像素点之间的约束关系,提升了一定区域的匹配精度,但其总体匹配精度仍然较低;Veksler[3]等提出了一种树形结构来替代传统的基于扫描行的DP方法,该方法更大地加强了扫描线内部及之间的约束,但匹配精度仍然不高。这些DP方法处理精度不高的一个重要原因是:在立体匹配的初始代价求取阶段,一般使用固定窗口进行能量聚集,这样仅仅以累加求平均的方式进行能量聚集,不能很好地体现像素与其周围各点的联系,且窗口的大小难以确定,得到的初始匹配代价仍存在较多误差。另外,在前向阶段及路径回溯阶段,对于每个像素点仅考虑了当前全局能量函数值E(d)最小的视差值。然而使当前点全局能量函数最小的视差值,并不一定就是使整条扫描线全局能量函数总和最小的视差值,因此这样做会导致一些有用信息丢失,甚至有可能会出现连续误匹配的现象。
本文针对传统DP算法存在的问题,对立体匹配初始代价求取、路径寻径及回溯加以改进。在初始代价求取阶段,提出了一种改进的变窗口能量聚集法,该方法通过获取场景的视差变化区域与视差连续区域的位置信息,从而使像素点在能量聚合时能够根据视差变化自适应地调整聚合窗口的大小,使能量聚合方式更加合理,提高了初始视差的准确性;在路径寻径及回溯阶段,使用多路径寻径回溯法,保留更多可靠点,避免了连续误匹配现象的发生。因此提高了立体匹配的匹配精度,并具有较好的实时性。
1 改进的多窗口能量聚合方法
1.1 初始匹配代价求取中存在的问题
初始匹配代价用于反映对应的匹配像素之间的相似程度,匹配代价值越小,两像素点为匹配点对的可能性就越大。匹配代价的计算就是利用相似性约束条件,对不同视差下立体图像对的基元进行相似度计算。
本文采用了Birchfield[4]等提出的BT相似性度量函数,可以减小对图像采样敏感程度,并且可以减少由于相关窗口整数像素匹配对精度的影响。
BT相似性度量函数如公式1所示

其中:

BT法原理示意如图1所示。该方法主要是对左右图像坐标分别为(x,y)和的 (x-d,y)待匹配像素点对进行邻域灰度线性插值,综合插值信息来进行匹配代价的计算。对于右图像而言,从插入的灰度值(x-d,y)、(x-d,y)和待匹配像素点的灰度值IR(x-d,y)找出最大值IRmax(x-d,y)和最小值IRmin(x-d,y),将左图像中的待匹配像素点IL(x,y)与右图像获得的最大值和最小值进行比较。如果IL(x,y)在IRmax(x-d,y)和IRmin(x-d,y)之间,那么左图像待匹配像素点到右图像待匹配亚像素点的匹配代价C(x,y,d,IL,IR)为0,否则对IL(x,y)与IRmax(x-d,y)的差值绝对值和IL(x,y)与IRmin(x-d,y)的差值绝对值进行比较,将较小值作为C(x,y,d,IL,IR)的值。同理,对左图像进行线性插值,获得右图像待匹配像素点到左图像待匹配亚像素点的匹配代价C(x,y,d,IR,IL)。最后比较两个匹配代价值C(x,y,d,IL,IR)和C(x,y,d,IR,IL),将较小值作为左图像坐标为(x,y)的像素点在视差为d时的匹配代价。
BT法在初始代价求取是具有优点,但若直接使用,在寻径时会产生多个相等的最优能量值,从而导致匹配的不确定性。因此需要将参考点与匹配点的邻域像素点信息引入进来,更全面地反映像素点的图像信息。能量聚合方法就是以参考点及匹配点为中心创建一个窗口,用窗口内相邻像素的亮度值分布来表征中心像素,从而体现中心点邻域像素间的关系,进而提高匹配准确率。

图1 BT法原理示意图
使用能量聚合法,首先需要建立合适大小的窗口。一般的能量聚合法是采用固定窗口对初始代价进行能量聚集,但这样做会带来固定窗口的大小难以确定的问题。窗口选取过小,在视差连续区域会造成较严重的误匹配;窗口选取过大,则会在视差明显变化区域造成较大误差,且会极大地增加计算量。
因此,初始代价聚集窗口大小要针对视差连续区域与视差变化变化区域相应处理。对于视差变化变化区域,像素周围各点的视差值变化较大,这时只需要一个较小的窗口,通过初始代价聚集即可得到较高质量的初始代价值。而对于视差连续区域,周围像素的视差均相等或接近,这时则需要一个足够大的窗口,以便涵盖足够多的像素点信息。
为了实现视差区域的划分,一般的能量聚合法采用如式(2)的判断方法[5],粗划分视差连续、变化区域。
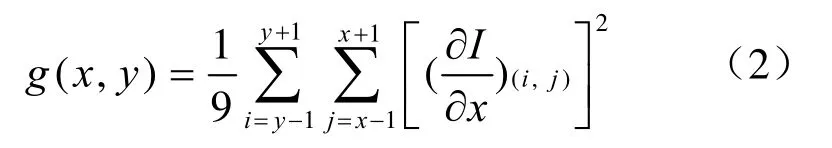
其中,(∂I/∂x)表示在(i,j)点处的水平梯度,设定阈值Tg。公式(2)其实是针对一个3*3窗口得到其中心像素的亮度梯度变化率。将亮度梯度变化率较大的区域定为视差变化区域,应用小窗口进行能量聚合,反之为视差连续区域,对其使用大窗口进行能量聚合。
但这种划分效果容易受到图像纹理因素的影响。物体表面的纹理也会造成梯度的变化,而纹理区域并不完全是视差变化区域,如黑白格子相间的地板图像,黑白格子的交界处属于纹理亮度变化区域,但是其视差与周围像素点都是一致的。如果将这些像素点当做视差变化区域点,应用小窗口进行能量聚集显然是不合适的。
1.2 视差变化区域的划分方法改进
视差变化区域主要是物体的边界区域,在真正物体的边界区域往往才会伴随着视差深度的变化,而物体表面的颜色纹理都应被排除。为此本文研究了一种改进的物体边界提取方法,首先获取实际图像的初步视差图,由于视差图上基本没有场景中物体表面纹理信息,因此通过视差图的亮度梯度变化对其进行边缘提取,即可较为容易地获得大致的物体边界图。再将该图与实际图像的边缘相匹配,滤除不能与之匹配的实际图像边缘,即可有效地提取出较准确的物体边界。在进行边界可靠提取后,就可以实现视差变化区域的有效划分。
边界提取的步骤如下:
1)对实际图像采用Canny算子提取边缘并保存;
2)使用WTA(Winner-Take-All,胜者为王)对前面的初始代价求取最小值,并通过一系列约束措施,得到初步视差图;
3)初步视差图含有很多单独的畸变点,采用基于信度的后处理方式将其滤除,得到一幅较为精准的初步视差图;
4)对步骤3)得到的初步视差图采用Canny算子提取边缘,获得初始物体边界图。然后再进行膨胀处理,增大可靠边缘范围,减少有用信息的丢失。
5)将步骤1)与步骤4)所得的两幅边缘图进行匹配,滤除不匹配的实际图像边缘,也即将步骤1)所得实际图像边缘图中未能与初始边界图相匹配区域全部置0,即可把实际图像边缘图转化为较为精准的物体边界图。
使用上述步骤进行边界提取会遇到如下两个问题:(1)使用WTA法求取初步视差图时,由于WTA法本身精度较低,得到的初始代价值误差较多;(2)获取的初步视差图中往往会存在单独的畸变点现象。
对于问题1,本文对最初取得的初始代价值添加如下一系列约束措施,以提高获得的初步视差图的精度:
1)在重复纹理区域,由于不同视差的匹配代价比较接近,初始视差代价值可能会出现多个极小值,从而引起误匹配。针对这一情况,首先求出当前点各视差下的最小代价C1,然后再求出次小代价C2,再定义C3=(C2-C1)/C1。当C3大于设定的阈值t1时,当前匹配被看作是可靠的,否则将其定义为不可靠匹配,并进行标记。也就是通过比较后把整个视差图进行分类,分成了标记点(不可靠匹配点)和未标记点(可靠匹配点)。
2)对未标记的点再进行唯一性约束处理。对于左图上的每个点,右图都有唯一的点与其对应。根据左图点x的最小匹配代价得出其对应的视差d1,x对应右图的点y=x-d1,即有匹配对L(x+d1,y)~R(x,y)。定义数组R[i],置R[y]=1。继续遍历x点,若发现存在匹配对L(x+d2,y) ~R(x,y),其R[y]值为1,即与之前存在的匹配对相冲突,不满足唯一性约束。此时分别比较两组匹配对的初始代价值,只保留初始代价值较小的视差值。
3)最后,对标记点统一进行处理,取其扫描线前一点的视差值作为当前视差值,从而获得初步视差图。
相比WTA法直接获取的视差图,使用上述约束后,场景视差图的视差深度变化信息得到了更好的反映,解决了WTA法初始代价值误差较多的问题,效果如图2所示。由图2可见,图2(a)存在较多的连续误匹配区域,而添加上述约束后,这些误匹配区域明显减少,如图2(b)所示。

图2 添加约束后WTA法实现效果比对图
对于问题2,也即获取的初步视差图中存在单独畸变点现象,本文在步骤3中采取一种基于可信度的后处理方式进行滤除。该方法分为以下6个步骤:
1)首先按列方向顺序地扫过视差图上的点,直至发现亮度变化区域或邻域的视差值比传播区域高2个级别以上方停止;
2)记录此时连续点的个数n,定义这些点的信度re值,令re=n;
3)继续扫过该列上其余的点直至该列被遍历为止;
4)按行顺序重复上述步骤进行遍历;
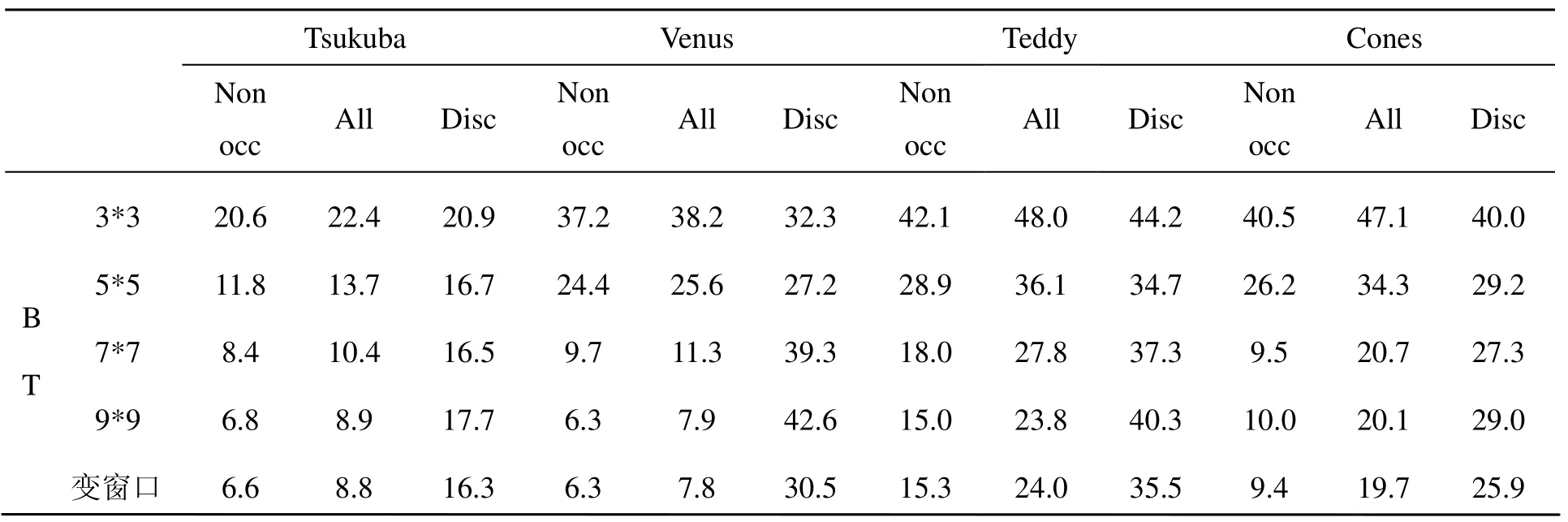
5)定义上阈值th与下阈值tl,对每个像素点基于此阈值进行信度分类。当re>th时,该像素被列为可信像素,re 6)将每个可信像素按列方向传播,当遍历到的区域不属于亮度变化区域时,覆盖其中的每个不可信像素的视差。 相较于处理前的初始视差图,整个图像处理后变得更加的平滑,图中的单独畸变点基本都可以得到很好的滤除,处理效果如图3所示。 图3 初始视差图滤除畸变点前后比较 改进的边界提取效果如图4(a-c)所示。其中图4(a)为对处理后的初步视差图提取边界并进行二阶膨胀处理的结果。图4(b)为原图直接使用Canny算子提取的边界图。图4(c)为将边缘图4(b)与初始边界图4(a)匹配处理后得到的物体边界图。图4(d)为场景实际边界图(无表面纹理的影响)。 图4 边界提取过程图 图4 (b)是直接使用Canny算子提取的边缘图,与场景实际边界图图4(d)比较,其表面纹理像素点个数为22238。而图4(c)是采用本文改进边界提取法得到的实际边界图,表面纹理点剩余个数为2810。相比之下,无用的表面纹理信息减少率为87.4%。将图4(c)与场景实际边界图4(d)进行比较发现,相同像素点所占实际边界图的百分比(即边界像素点保持率)为88.5%。可见使用本文方法物体边界信息得到了很好保留,物体表面纹理等无用信息得到很好的滤除。 在进行边界可靠提取后,即可实现视差变化区域的有效划分。对视差变化大的区域应用5*5小窗口进行能量聚合,防止引入过多不必要的像素邻域信息。对视差变化小的区域应用9*9大窗口进行能量聚合,尽可能多地引入中心像素点的有用邻域信息。 通过按视差变化情况进行能量聚合,获得的各像素点在不同视差下的初始匹配代价值具有更高的精度。 基于动态规划的立体匹配算法的实质就是要在视差空间图像上求出一条最优路径,使能量函数E(d)(式3)取值最小。其中Edata(d)是初始代价值,Esmooth(d)是平滑项。 一般DP算法在处理前向阶段时,对于每个像素点仅会考虑使其代价值E(d)最小的匹配转换方式,忽略掉那些即使与最小代价相差很小的转换方式。并且,在路径回溯阶段,也只考虑使图像最后一列上的点代价最小的转换方式,来作为路径的结尾,这样做法必然会导致大量有用信息的丢失。因为使最后一列上的点代价最小的转换方式,并不一定是最优路径的结尾方式。同样,前向过程中各点在各阶段视差值下最小代价值的累加也不一定就是最优路径的匹配代价值。若在扫描线上存在畸变或误匹配点,若以该点最小代价视差作为前向指导后续点进行匹配,则有可能会出现连续误匹配的情况。为了更多地保留正确信息,提高匹配精度,在前向阶段,把与最小代价相差小于常数阈值Rd的转换方式,作为可能路径项加以存储;在路径回溯阶段,除了使结尾点代价为最小值min的转换方式保留外,凡是代价Cost<α*min(α为常数,且α>1)的转化方式均加以保留,并以其为可能的路径结尾进行回溯。 该过程用伪代码表示为: 其中C(x,d)为像素点x在视差大小为d时的匹配代价,S(x,d)为扫描线至点x时总匹配代价。将与最小匹配代价相差在一个很小阈值Rd范围内的视差也加以保留(包括匹配代价C(x,d')与总代价S(x,d')),作为扫描线下一像素点的可能前向进行寻径。 在视差寻径求取阶段使用多路径寻径法,可以保留更多的可能视差值,从而获取更多的有效视差信息,避免横向寻径时由于单个点的误匹配,而造成后续扫描线上连续误匹配的状况,提升了匹配的可靠性。 首先对初始代价求取阶段的改进算法效果进行了验证,采用BT法分别使用大小为3*3、5*5、7*7和9*9的固定窗口以及变窗口进行立体匹配,得出初始视差图,如表1所示。可以看出:使用固定窗口进行立体匹配,随着相关窗口的增大,与周围整体像素亮度差异较大的离散点(图中的分散白色像素点)的数目逐渐减少,表明随着相关窗口包含信息量的增加,像素点的匹配准确性也随之提高。但当窗口增大时,图像中物体的边缘出现了膨胀现象,边缘定位也较为模糊。而采用可变窗口得出的视差图,离散点数目较少,且物体边界区域较为清晰,综合效果更佳。表2为BT法在不同窗口大小情况下获得的视差图误匹配率比较,通过该表可看出:采用固定窗口时,随着窗口大小的逐渐增大,非遮挡区域和所有区域的误匹配率逐渐降低,但深度不连续区域的误匹配率先降低后升高。也即相关窗口信息量增多在提高深度连续区域匹配精度的同时,边缘定位准确性逐渐降低。而变窗口法各项匹配精度较高,尤其是视差不连续区域匹配精度更高。 本文向标准的测试平台http://vision.middlebury.edu/stereo/)提交了最终实验结果。表3为改进DP算法与国外一种DP改进算法ReliabilityDP法对标准图的处理效果比较,表4为经测试平台评估计算的匹配结果误差率比对情况。 表1 不同窗口下BT法获得的视差图 表2 不同窗口下BT法获得的视差图误匹配率比较 表3 采用Middlebury标准图的实验结果 表4 立体匹配算法的精度比较 本文算法属于DP算法,计算速度较快,通过相应的改进措施又获得了较高的匹配精度。由表4的各项指标比较可看出,本文算法匹配精度高于ReliabilityDP等一些DP算法,且高于部分高计算量的算法,如GC算法等[6]。文献[7-8]提出的optimizedDP法与RealtimeCensus法等均是近一年来国外提出来的精度与速度并重的匹配算法,本文在精度上要高于这些算法。对于文献[9]提出的高精度大计算量匹配算法,本文算法虽然在整体精度上低于该算法,但对后两幅大视差图像的处理精度要高于该算法。 本文针对传统DP方法处理精度不高的问题,在DP算法的初始匹配代价求取阶段、路径寻径及回溯阶段加以改进。相较于一般的DP算法,本文算法的匹配精度得到了很大的提高,并具有较好的实时性,能更好地满足实际应用中对立体匹配算法实时性与准确性的要求。 [1]Geiger D, Ladendorf B, Yuille A. Occlusions and binocular stereo [J]. International Journal of Computer Vision, 1995, 14(3): 211-226. [2]Gong M, Yang Y H. Near real-time reliable stereo matching using programmable graphics hardware [J].IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005, (1): 924-932. [3]Veksler O. Stereo correspondence by dynamic programming on a tree [J]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 2005, (2): 384-390. [4]Birchfield S. Depth discontinuities by pixel-to-pixel stereo [J]. International Journal of Computer Vision,1999, 35(3): 269–293. [5]Daniel S, Richard S. A taxonomy and evaluation of dense two-frame stereo correspondence algorithms [J].International Journal of Computer Vision, 2002, 47(1):7-42. [6]Boykov Y, Veksler O, Zabih R. Fast approximate energy minimization via graph cuts [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(11): 1222-1239. [7]Salmen J, Schlipsing M, Edelbrunner J. Real-time stereo vision: making more out of dynamic programming [C]//. Computer Analysisi of Images and Patterns, beRLIN: 2009: 1096-1103. [8]Humenberger M, Zinner C, Weber M. A fast stereo matching algorithm suitable for embedded real-time systems. Computer Vision Image Understanding, 2010,114(11): 1180-1202. [9]李彬彬, 王敬东. 基于图像分割的置信传播立体匹配算法研究[J]. 红外技术, 2011, 33(3): 167-172.

2 改进的动态规划多路径寻径法
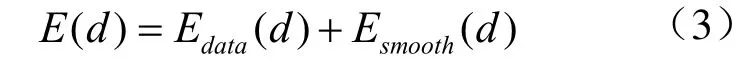
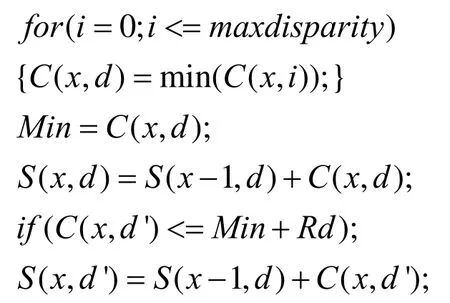
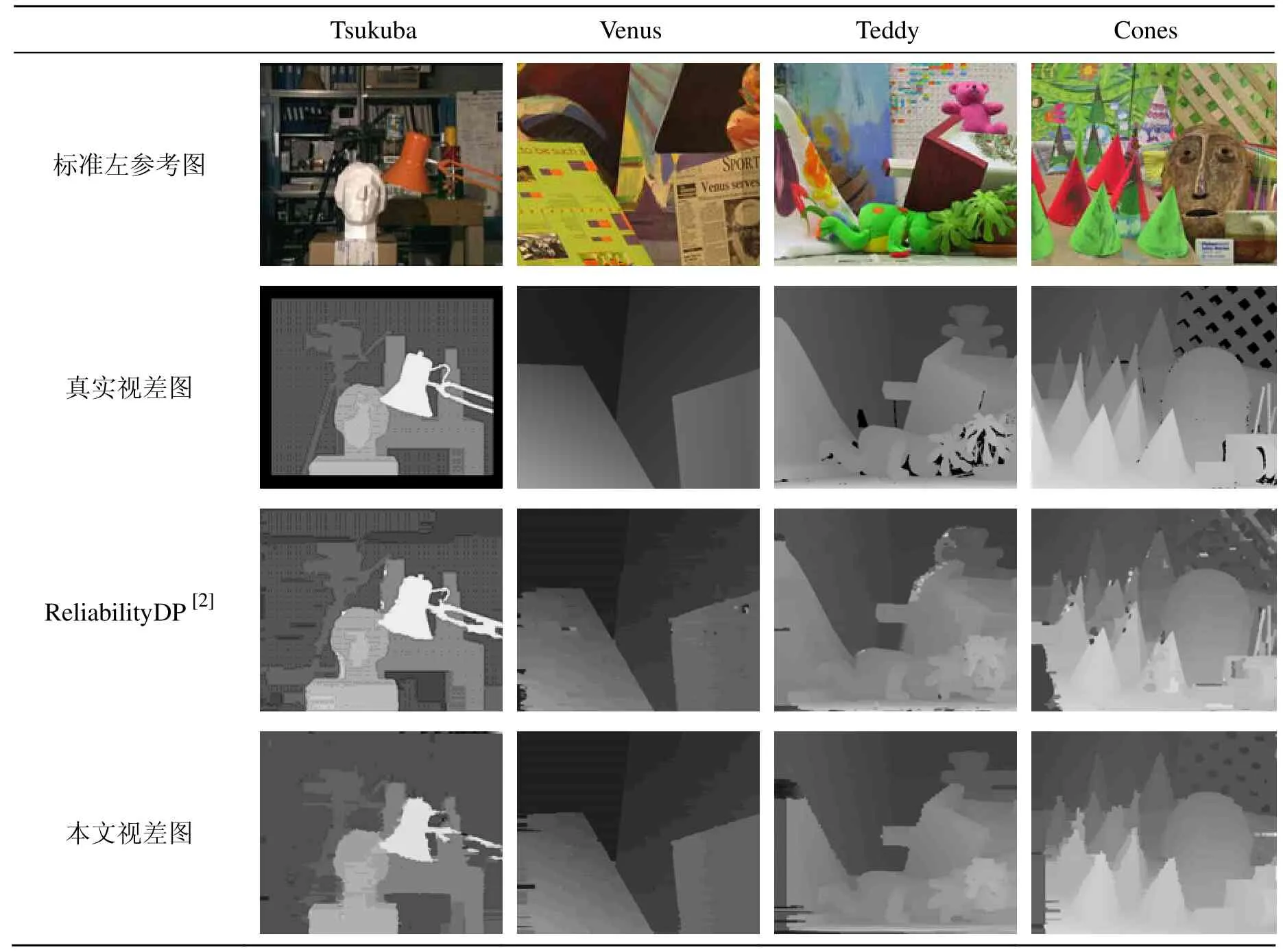
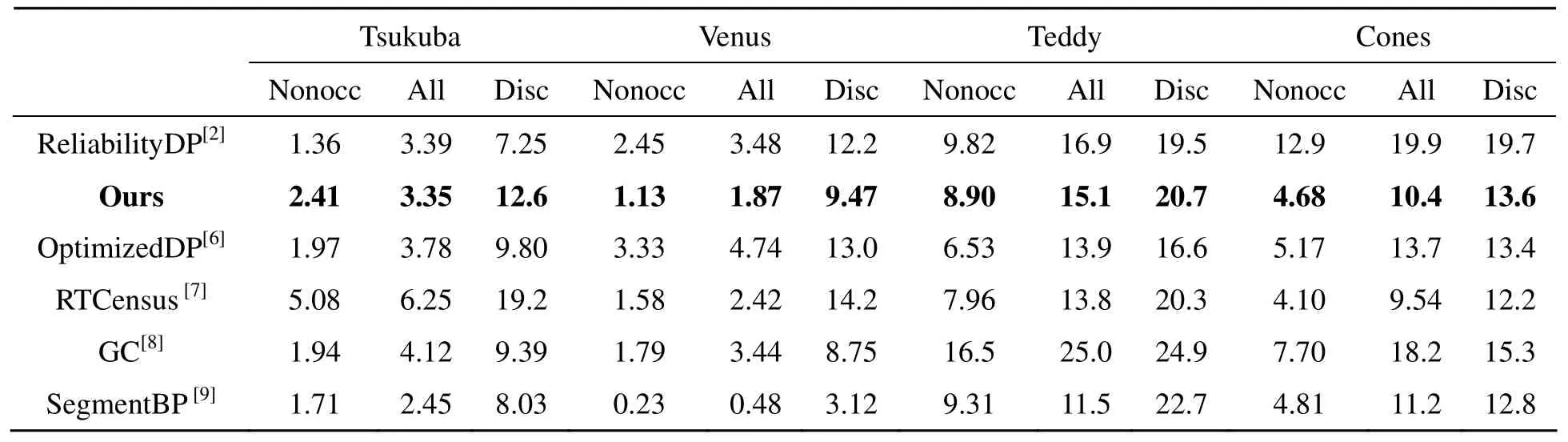
3 实验结果与分析

4 结 束 语
