基于特征轮廓的立体构型方法
2013-03-21张秀芝张云辉侯洪生
张秀芝, 闫 冠, 张云辉, 侯洪生
(吉林大学机械科学与工程学院,吉林 长春 130025)
培养学生读立体的二维视图的能力和进行立体构型的能力是工程图学课程的基本内容之一。传统工程图学课程中立体部分知识的授课方式是通过模型加挂图以及教师的语言描述加学生的想象力来完成的。三维CAD软件引入工程图学的课堂教学中,使得传统教学方式产生了革命性的变化[1]。三维CAD软件的使用不仅能够形象的展现立体的成型过程,而且为立体构型分析提供了新的思路[2],本文结合工程图学和三维CAD软件的教学实践,总结出一种基于特征轮廓的立体构型方法。
1 特征轮廓
工程图学课程中的常见立体结构多可看成是平面图形按照一定的规则运动而成[3-4]。图1所示立体的构型过程可看成是平面图形沿着与其自身垂直的方向拉伸形成。图2所示立体则可看成是平面图形绕着与其在同一平面内的轴线旋转而成。这些平面图形决定了立体的形状。
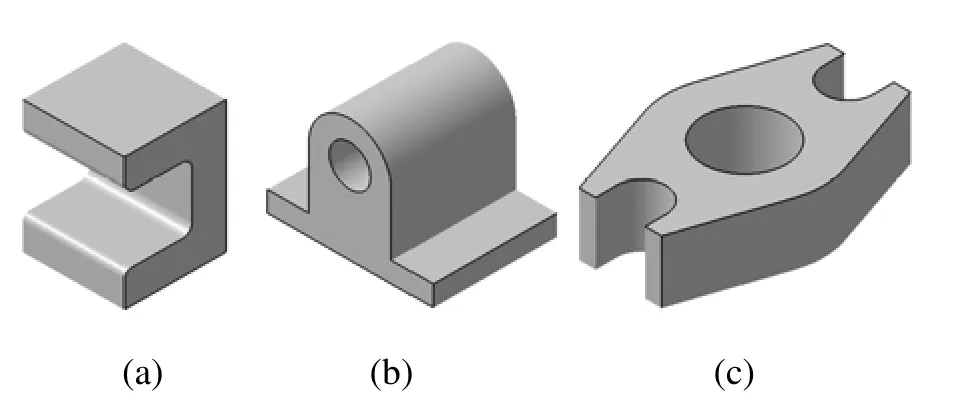
图1 拉伸构型柱体
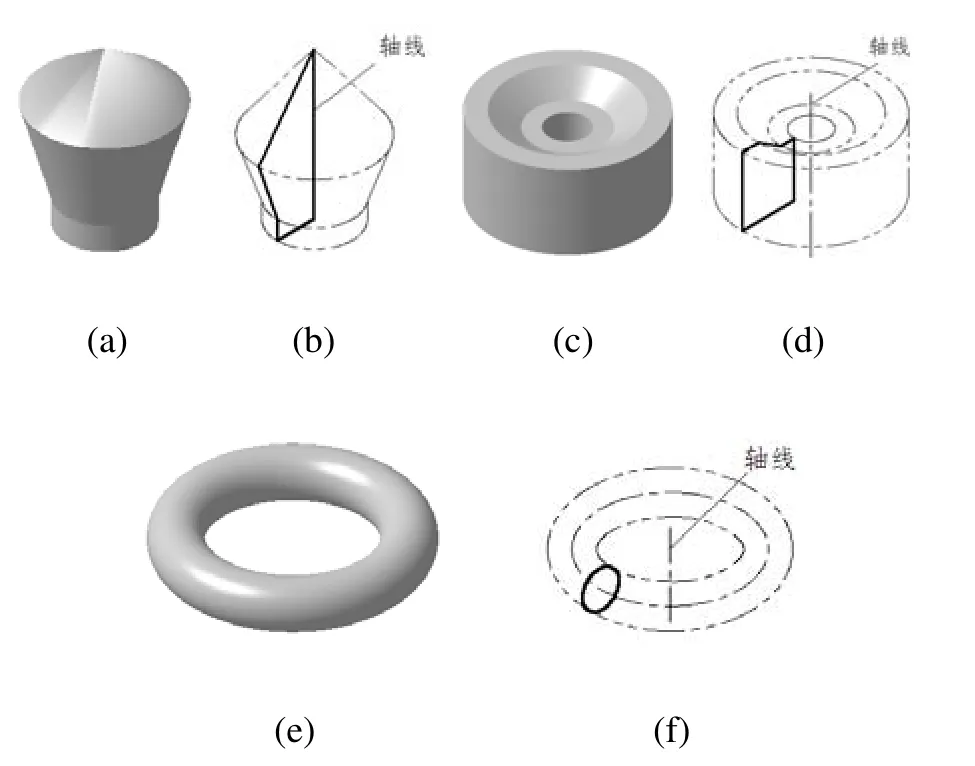
图2 旋转构型回转体
这里将决定立体全部或部分结构形状的平面图形称为特征轮廓。若要通过读立体的二维视图想象还原出立体形状,可以首先从二维视图中找到决定立体结构形状的特征轮廓。立体某一方向上的最外边界或者内部的封闭图形都可以成为立体构型的特征轮廓,特征轮廓的形状可以是多边形、圆或一般平面图形。有些立体只有一个特征轮廓,有些立体则在某一个方向上有多个特征轮廓或在不同方向上都存在特征轮廓。
2 单特征轮廓
图1和图2中立体的形状由单特征轮廓决定。
2.1 单向单特征轮廓
图3为图1所示立体的三视图。从中可以看出,图3(a)的主视图能够反映该立体的形状特征,是立体的特征轮廓,立体的成型过程可理解为XZ面上的特征轮廓沿Y方向拉伸成型;图3(b)的左视图为立体的特征轮廓,立体由YZ面上的特征轮廓沿X方向拉伸成型;图3(c)所示立体的成型过程则是XY面上的特征轮廓沿Z方向拉伸成型。图3所示立体都是单特征轮廓沿单一方向经拉伸形成,可统称为拉伸柱体。

图3 单向单特征轮廓拉伸柱体
2.2 旋转特征轮廓
图4 为图2所示立体相应的主视图和俯视图,对照图4(a)和图2(b)可以看出,以主视图的1/2这个平面图形绕自身的一条边旋转一周形成该立体,这条边则成为立体的轴线。图4(b-c)和相对应的图2(d-f)则展示了平面图形绕与其共面且和该平面图形不相交的直线旋转形成立体,该直线即是立体的轴线。形成旋转立体的基础图形可称之为旋转特征轮廓。单特征轮廓经旋转形成的立体可统称为复合回转体。
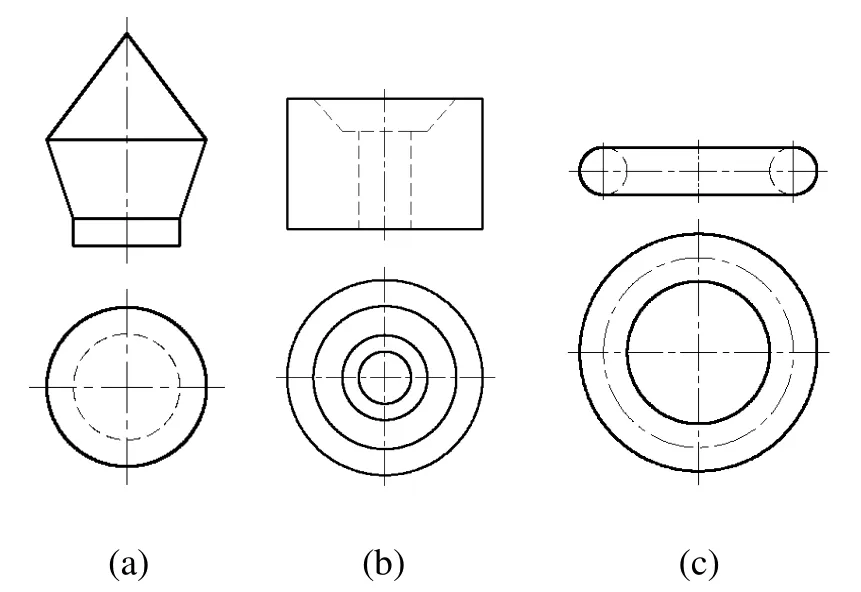
图4 特征轮廓旋转构型的复合回转体
3 单向多特征轮廓
3.1 单向对称多特征轮廓
很显然,图5(a)的左视图代表了立体的形状特征,该立体是由图5(b)和图5(c) 2个处于立体对称面上且上下相接的2个特征轮廓沿着同一方向对称拉伸不同的长度而成的。

图5 单向对称特征轮廓
3.2 单向多层次特征轮廓
图6 (a)以主视图和左视图2个视图表现了一个立体,从左视图可以看出此立体在Y方向上有3个层次,而主视图中则体现了每个层次的形状特征。所以可以从主视图中提取出每个层次的特征轮廓,如图6(b)所示。最外特征轮廓沿着Y方向拉伸一定的宽度后,次大的特征轮廓继续拉伸一定宽度,最小的特征轮廓沿着同一方向拉伸一定宽度,如图6(c)所示。这里每一个宽度层次上有一个特征轮廓,这些轮廓都是通过拉伸的方式生成立体结构。

图6 单向多层次拉伸特征轮廓
一个特征轮廓经过拉伸后所生成的新表面上,还可以有同一方向上的通过切割的形式在立体上生成新结构的特征轮廓,如图7所示,这些特征轮廓构成新的层次。
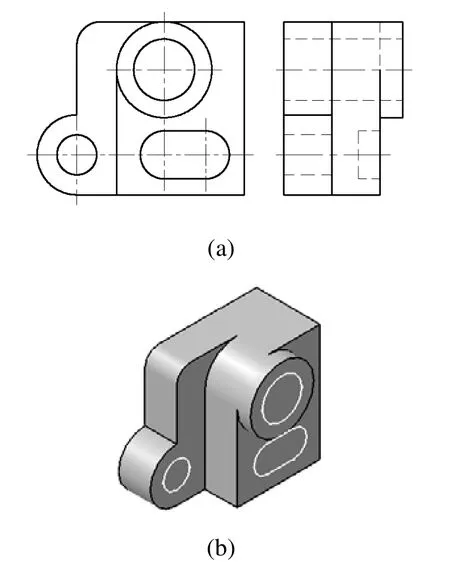
图7 单向多层次切割特征轮廓
4 双向单特征轮廓
如图8(a)所示立体,在工程图学课程中通常将其看成是由棱柱体经多次切割而成,或者由几个基本立体堆叠而成。
将三维实体构型的思想和特征轮廓的思路结合起来考虑,图8(b)主视图和左视图的最外边界可以看成相互垂直的两个特征轮廓。如图8(c)所示,沿各自的法线方向,一个看成是拉伸,另一个看成是切割,两个动作组合成型。这个组合成型过程相当于图8(d) 和图8(e) 2个单一方向拉伸柱体的布尔交集。

图8 双向单特征轮廓(多边形组合)
这种由立体的两个二维视图提取出最外边界作为特征轮廓,再分别沿其法线方向一个作为拉伸轮廓一个作为切割轮廓组合构型的方法可以称作双向单特征轮廓法,主要有以下几种类型:
(一个约定:由直线和曲线共同围成的图形投影相对复杂,应用双向特征轮廓法时为将其与其他图形区分方便,将这类图形称作“复合平面图形”。)
4.1 多边形与多边形组合
图8中的立体即是2个多边形特征轮廓一个作为拉伸轮廓、另一个作为切割轮廓而成型的。
4.2 多边形和圆形组合
图9所示立体的主视图为一多边形,左视图最外边界为圆形,用双向特征轮廓方法,分别以多边形和圆形作为特征轮廓沿各自法线方向,一个方向拉伸,另一个方向切割,即形成该立体。图9(a)左视图中圆的直径和多边形的高方向尺寸相等,也就是立体的高。
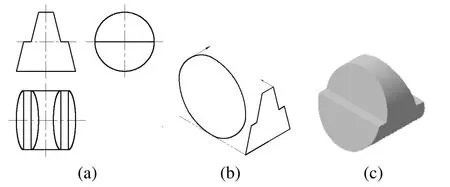
图9 多边形和圆形等高组合构型
将图9中立体左视方向的圆直径增大如图10(a)所示,应用双向特征轮廓方法则得到形如图10(b)所示立体,其三视图如图10(c)所示。从主视图和左视图中分别提取出最外边界作为特征轮廓,成型过程如图10(d)所示,同样得到图10(b)所示立体,即图10(a)和10(d)中的圆形被截与否并不影响立体结构。所以在教学实践中,讲授读立体的二维视图时采用图10(d)可以帮助学生快速准确的想象出立体的形状,而在讲授三维立体建模时则采用图10(a)的特征轮廓可以简化立体建模过程,节省时间。

图10 多边形和圆形不等高组合构型
4.3 多边形和平面图形组合
图11 (a)所示的底板结构,用传统的立体构型方法分析,可以看成是叠加在一起的两块板,对称的以上下方向切割两个U型结构而成。从图11(b)给出的立体三视图分析,俯视图的最外边界是一个由多段直线和圆弧围成的复合平面图形,左视图的最外边界为多边形,二者分别代表了立体上下方向和左右方向的形状特征,用双向特征轮廓的方法构型,一个作为拉伸轮廓而另一个作为切割轮廓进行构型,如图11(c)所示,即可得图11(a)的立体结构。
此例中将左视特征轮廓作为拉伸轮廓而俯视特征轮廓作为切割轮廓,较容易想象立体结构。
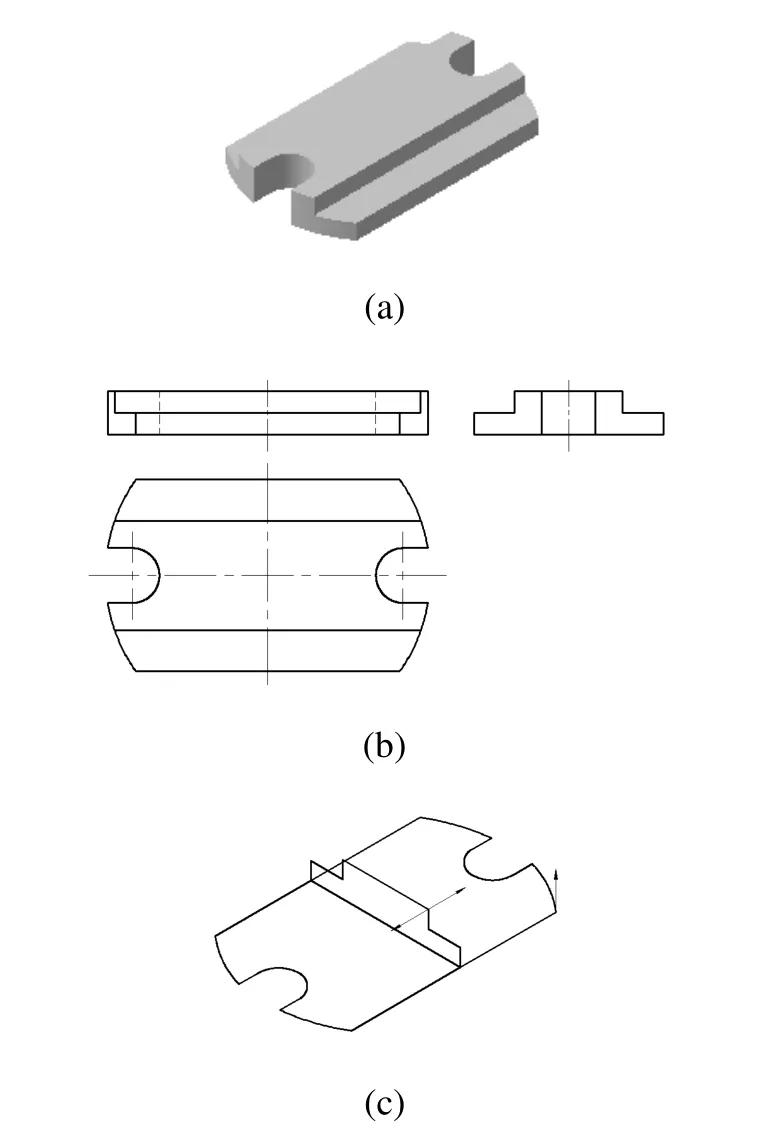
图11 多边形和复合平面图形组合
4.4 圆形和圆形组合
图12 (b)为图12(a)所示立体结构的三视图,经分析,主视图不能代表立体的形状,而立体的俯视图和左视图是直径相同的2个圆,显然俯视图和左视图的2个圆形轮廓代表了立体的形状特征,因此,此2圆可作为立体构型的双向特征轮廓,一个作为拉伸特征轮廓另一个作为切割特征轮廓,如图12(c)所示,即可构型。
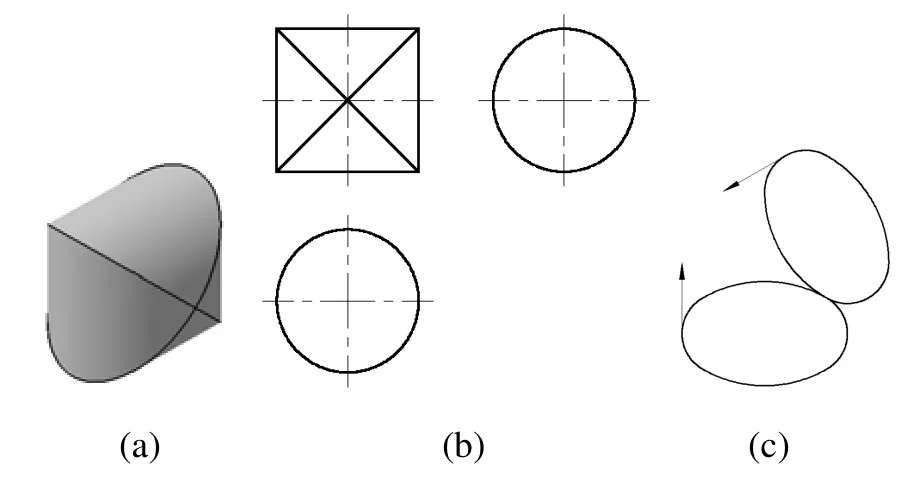
图12 直径相同的圆轮廓组合
增大图12(c)中上下方向圆的直径如图13(a)所示,应用双向特征轮廓成型方法得到图13(b)所示的枕形结构,其三视图如图13(c)所示。单独观察分析立体的三视图,其俯视图和左视图代表了立体的形状,将其作为双向特征轮廓,一个方向拉伸,一个方向切割,如图13(d)所示,同样得到图13(b)的立体结构。笔者的体会是将小直径的圆轮廓看成是拉伸轮廓而大直径的圆轮廓看成切割轮廓更容易想象立体的结构。类似文中4.2的分析,在实践中图13(a)和图13(d) 2种思路可以灵活运用。

图13 直径不同的圆轮廓组合
图14 和图15分别是圆形和复合平面图形以及两个复合平面图形作为双向特征轮廓构型的简单示例,不再详细说明。
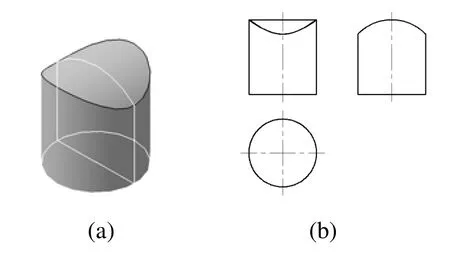
图14 圆形和复合平面图形组合

图15 两个复合平面图形组合
应用双向单特征轮廓方法进行立体构型分析时,有一个一般性规律,当两个方向的特征轮廓复杂程度差别较大时,将较复杂的特征轮廓看成是拉伸轮廓而较简单的特征轮廓看成是切割轮廓想象还原立体结构较为容易和快速。
5 双向多特征轮廓
双向多特征轮廓是指两个构型方向上至少有一个方向上有两个以上特征轮廓来决定立体结构的情况。图16(a)所示立体经图16(b)提取出主视图和俯视图的最外边界作为特征轮廓应用双向单特征轮廓方法的构型结果如图16(c)所示。
对照图16(c) 进一步分析图16(a),可见主视图上部左右两个直角三角形进一步决定了立体的完整形状,所以将此两直角三角形提取出来作为和主视图最外边界在同一方向上的新一层的特征轮廓,如图16(c)所示,经过切割成型最终完成立体构型,如图16(d)所示。象这样的成型过程可称作双向多特征轮廓法。

图16 双向多特征轮廓构型
6 构型分析实例
机械零件的构型中,前面所提到的方法有时单独使用即可,对于结构复杂的零件往往需要两种或两种以上的方法联合使用才能完成。图17(a)为某型号的空气压缩机中活塞的结构视图。总体上可将活塞结构分为四个大部分,即活塞头部、圆筒部分、连接部分和导柱部分。活塞头部大体上是回转结构,通过视图分析,其左视图中内外轮廓的一半可以作为旋转特征轮廓,以自身一条边作为轴线旋转一周成型,如图17(b-c)所示。中间部分圆筒结构可从左视图中提取出类同心圆作为拉伸特征轮廓,从A向视图中提取其最外边界作为切割特征轮廓,应用双向单特征轮廓方法一次构型完成,如图17(d-e)所示。其余结构较简单在此不再赘述,最终完成的立体构型如图17(f)所示。
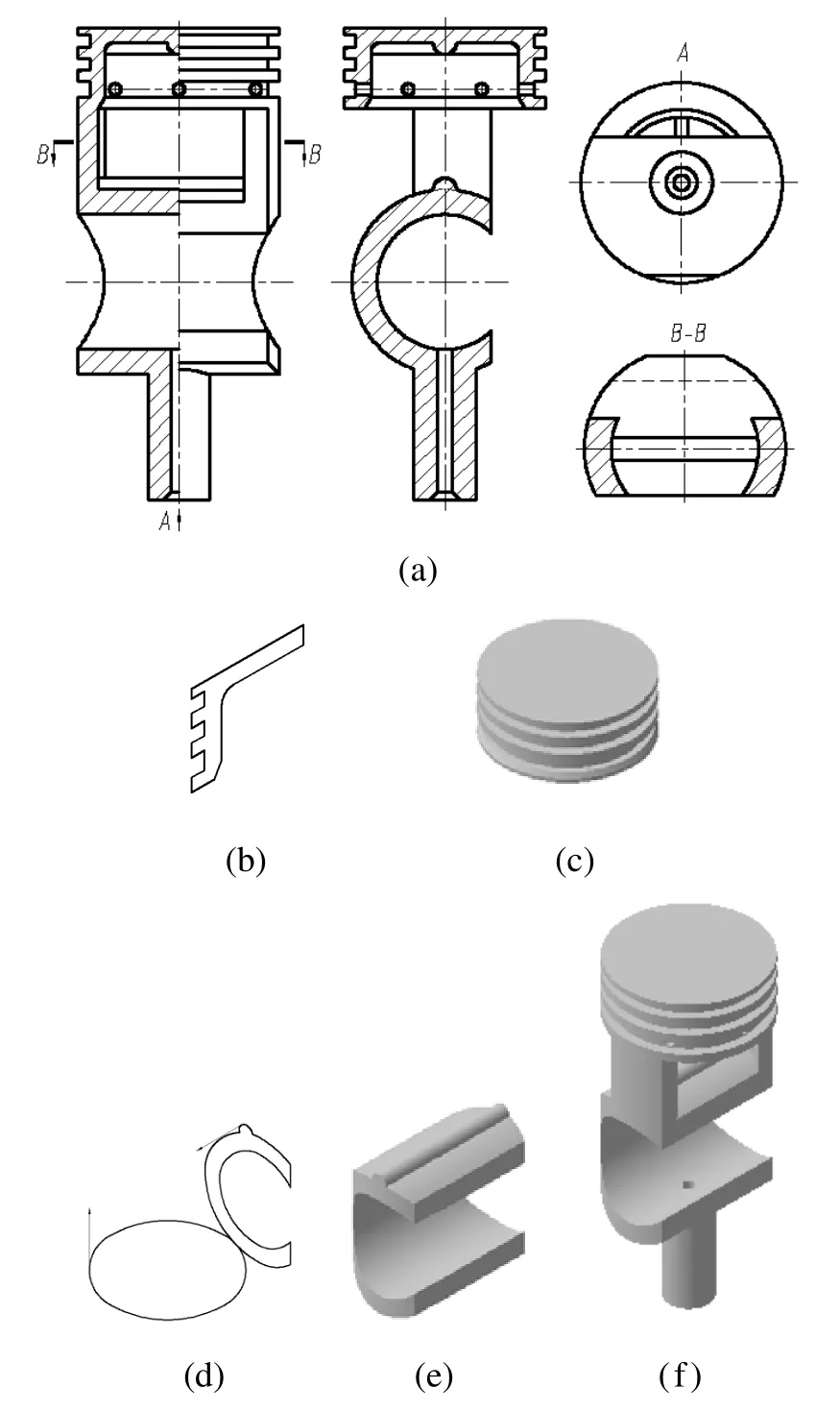
图17 活塞的构型分析
7 结 束 语
特征轮廓法可以解决由投影面平行面和投影面垂直面经过拉伸、切割或者旋转的方式生成的立体结构的读图和构型问题,为工程图学课程中立体的读图问题提供了新的方法,可以拓宽学生的想象空间,强化学生的空间思维能力。应用特征轮廓法,尤其双向单特征轮廓法,可以简化立体三维构型过程。
特征轮廓法不仅可以用于工程图学系列课程的教学,而且为立体的实体造型和生产加工过程提供了新的思路。
[1]张京英, 罗会甫, 张 彤, 等. 三维造型设计与工程图学的有效融合[J]. 工程图学学报, 2010, 31(6):151-154.
[2]唐荣锡. CAD/CAM技术[M]. 北京: 北京航空航天大学出版社, 1994: 149-159.
[3]侯洪生, 闫 冠, 谷艳华. 由二维视图复原三维立体的新方法[J]. 工程图学学报, 2011, 32(3): 95-99.
[4]侯洪生, 王秀英, 王泰花, 等. 机械工程图学[M].北京: 科学出版社, 2008: 30-38.
