一种基于子采样的混合域稳健零水印算法
2013-03-21韩绍程张兆宁
韩绍程, 张兆宁
(1. 中国民航大学基础实验中心,天津 300300;2. 中国民航大学空中交通管理学院,天津 300300)
数字水印技术作为图像版权保护的有效手段,近年来一直受到研究者的广泛关注。常见的数字水印技术,大多是通过修改系数的方式在图像的空域或变换域中秘密地“加入”水印信息(版权信息、用户信息等)来标识图像的版权。这类方法难免会让图像产生一定程度的失真,并导致水印稳健性和不可感知性之间的矛盾[1]。文献[2]提出的零水印方案能够有效地解决这一问题,所谓“零水印技术”就是在对原始图像数据不进行任何修改的前提下,利用图像固有的本质特征来构造具有唯一标识性的零水印,将生成的零水印或零水印加密处理后的结果在IPR(Intellectual Property Rights)信息数据库中注册,以用于水印的提取。目前,一直有不少研究者从事零水印的研究,Zhou[3]对图像小波变换后的低频分量进行分块奇异值分解,通过比较相邻子块最大奇异值之间的大小关系构造零水印。Yang[4]等先将图像进行分块DCT变换,并选择出一部分子块,通过比较所选每个子块DC系数和所有子块DC系数均值之间的大小关系构造零水印。
2007年K. Guo等[5]通过特殊形式的具有合成膨胀的仿射系统构造了剪切波变换 (Shearlet transform)。作为一种新颖的后小波分析方法,剪切波变换不仅能像曲线波变换一样,对图像提供最优逼近,而且可以在多分辨率分析框架内实现。同时,与轮廓波变换(CT)和非下采样轮廓波变换(NSCT)相比,剪切波在剪切过程中没有方向数和支撑基尺寸大小的限制,并能拥有更高效的计算效率[6]。近年来剪切波变换在图像融合、图像去噪及目标边缘检测等图像处理领域中已经取得了一定的研究成果[7~9]。然而,这些研究大多是采用下采样策略实现剪切波变换的离散化,由于不具有平移不变性而易产生伪吉布斯现象。非下采样剪切波变换(NSST)[10]就不存在这样的问题,其将会在图像处理研究方面发挥更重要的作用。
图像离散余弦变换(DCT)后的直流分量DC具有很好的能聚作用,其数值具有一定的稳定性。本文将这一特点与NSST技术相结合,提出了一种基于子采样的混合域稳健零水印算法。对图像NSST分解后的低频分量进行子采样得到4幅子图,随机选择2幅子图进行分块DCT变换,通过比较对应子图中规定映射位置上的DC系数的大小关系构造零水印。实验结果表明,该方法能有效地保护数字图像的版权。
1 相关理论
1.1 剪切波变换
当维数为2 时,具合成膨胀的仿射系统定义为:
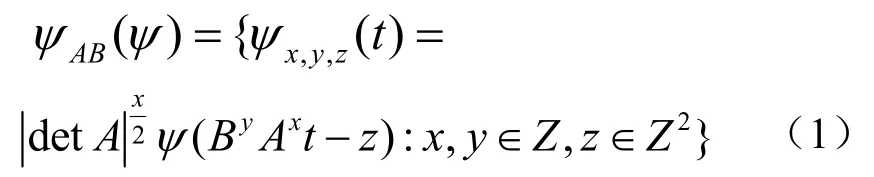
剪切波变换应用于图像处理时,需采用其离散化形式。非下采样剪切波变换的离散化过程主要分为多尺度剖分和方向局部化两个步骤,多尺度剖分由非下采样金字塔滤波器(NSPF)实现,方向局部化是通过剪切滤波器(SF)来完成,由于非下采样剪切波变换在图像分解和重构过程中避免了下采样和上采样操作,从而具有平移不变性[10]。
1.2 DCT变换
二维DCT是先将图像分成N×N像素块,然后对N×N像素块逐一进行DCT变换。N×N像素矩阵f(i,j)的二维DCT变换的定义为:
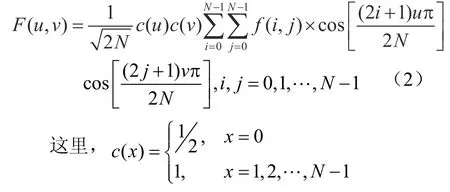
2 算法描述
2.1 零水印构造
设原始载体图像为I,其大小为M×M,水印信息为W,大小为n×n,则零水印的具体构造过程如下:
1)将图像I进行非下采样Shearlet变换,提取出低频分量记为A,其大小仍为M×M。
2)对A进行子采样操作得到4幅子图,记为A1,A2,A3,A4,其大小为M/2×M/2。

3)分别对A1,A2,A3,A4进行c×c的分块DCT变换,并提取每个子块的DC系数组成新的系数矩阵记为B1,B2,B3,B4,这里c=M/2n。
4)使用密钥key1生成随机序列Zk={(i,j)},其中i,j={1,2,3,4}且i≠j,作为系数选择器,k=1,2,…,n2。
5)借助logistic系统(见公式(4))生成混沌序列X={xi, 1≤i≤m2,m>>n},从中选取n2个不重复的元素组成新的序列D,并对其进行升序排列,即[EIX]=sort(D),这里E为排序后的序列,IX存放了排序后元素在D中的位置信息。
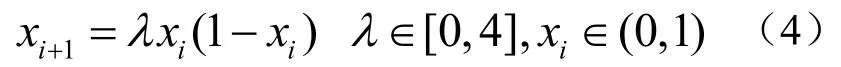
6)按照以下规则构造零水印

其中,k=1,2,…,n2;i,j为Zk中的数值。
7)把W′扫描成矩阵的形式W″,并与原始水印图像W进行异或运算,生成注册中心水印,作为水印提取时的密钥:

2.2 水印提取
设遭受击后的载体图像为I′,水印提取过程与零水印构造过程相类似,即:
1)按照2.1中式(1)~式(3)描述的方法从待检测图像I′中获得待比较的系数子集
2)使用相同的密钥key1生成随机序列Zk={(i,j)}。
3)按照2.1式(5)生成矩阵IX,并按照如下规则提取零水印:
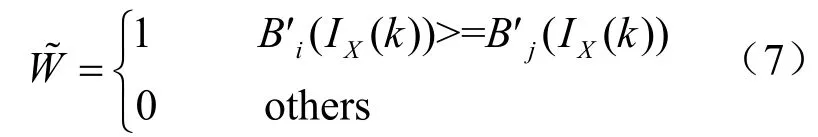
4)把先扫描成矩阵形式,最终提取出水印信息:

3 实验结果
采用大小为512×512的Lena、Baboon和Peppers三幅纹理程度不同的灰度图像作为测试图像,如图1所示,采用大小为64×64的带有“信息安全”字样的二值图像作为水印图像,如图2所示。

图1 原始载体图像
采用峰值信噪比(PSNR,见公式(9))来评价图像遭受不同攻击后图像视觉质量的变化,PSNR值越小,表明图像遭受到的破坏就越大,这时攻击前后图像视觉质量的变化就越明显。一般情况下,灰度图像PSNR值大于45时视觉上与原始图像相比无明显差异。提取出的水印图像W*和原始水印图像W之间的相似度用归一化相关(NC)值来度量,NC值越大,则两者相似度越高。NC的定义见公式(10)。
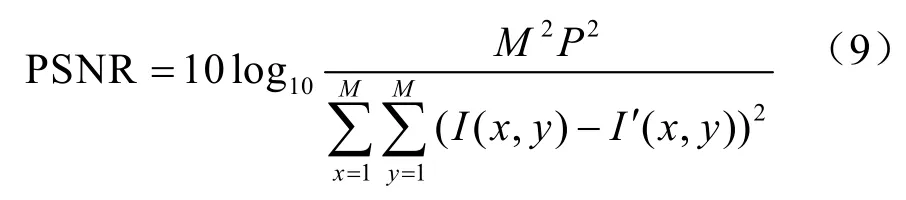
其中,M表示图像的大小,P是信号峰值,I和I′分别为攻击前后的图像。
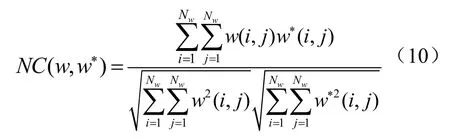
其中,w代表原始水印信息,w*表示提取出的水印信息,Nw为水印的大小。
3.1 稳健性测试
为了验证算法的稳健性,选取8种常见的攻击,其依次为:(a) 强度为0.01的高斯噪声;(b)强度为0.03的椒盐噪声;(c) [8×8]中值滤波;(d)30%JPEG压缩;(e) 缩放处理512-128-512;(f) 左上角1/8 剪切;(g) 向右旋转1°;(h)向下平移5行。图3显示了Lena图像在遭受这些典型攻击后的视觉效果和相应的PSNR值,不难发现,Lena图像经历过(a)~(h)这些攻击后,视觉已经质量严重受损,与攻击前的Lena图像相比存在明显差异。图4分别显示了采用本文算法从图3所示Lena经历不同攻击后的相应图像中提出的水印信息。由图4可见,提取出的水印信息清晰可见,表明该算法具有较强的稳健性。

图3 对应攻击下的图像及PSNR值

图4 对应攻击下提取的水印信息
3.2 算法性能比较
为进一步说明本文提出的算法对不同纹理图像的适应性以及非下采样剪切波变换相对于其他多尺度变换的优越性,将算法中的NSST分别用离散小波变换(DWT)、离散多小波变换(DMWT)和非下采样轮廓波变换(NSCT)替换,获得对应的低频分量,并进行了大量的仿真实验。同时,需要指出,在前两种替换方案中c=2,而在NSCT+DCT方案和本文算法中c=4,目的是保证构造零水印和提取水印大小的一致性,从而便于方案比较。表1显示了不同混合域方案下从遭受(a)~(h)攻击后的Lena图像中提取出水印的NC值。图5和图6分别以Baboon和Peppers作为载体图像,对比了相同攻击下采用不同混合域方案提取出水印的NC值。表1以及图5和图6,共同表明,本文提出的NSST+DCT混合域零水印构造和提取方案具有一定适应性。针对不同的图像,采用该方案均能够提取出相似度较高的水印信息来,且较其他混合域的替代方案相比在算法稳健性方面更具优势。
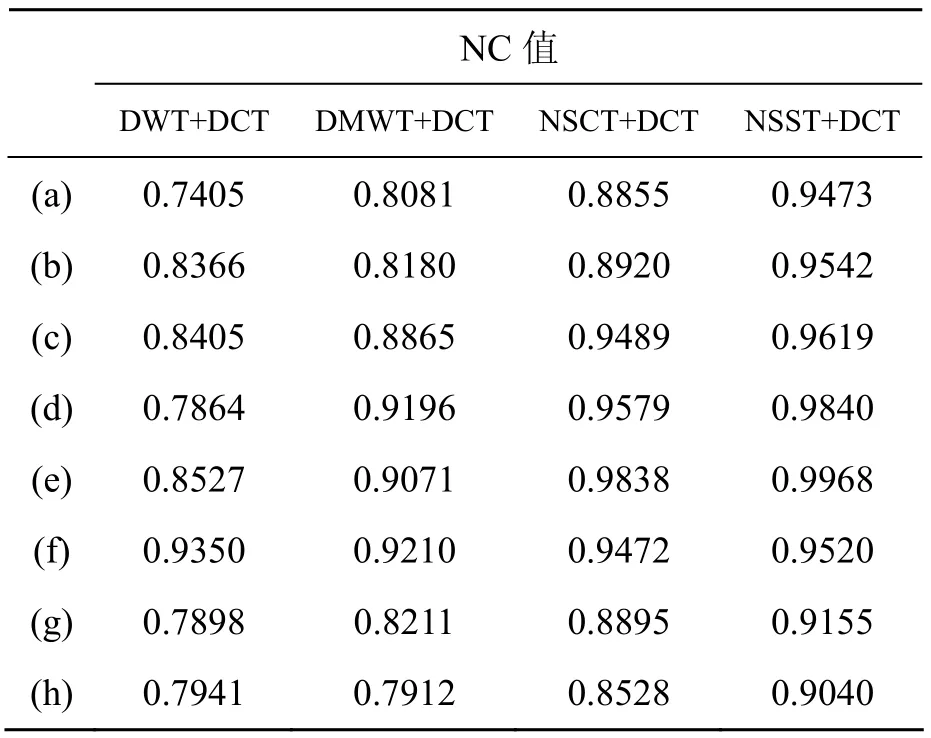
表1 Lena图像下不同混合域算法性能比较
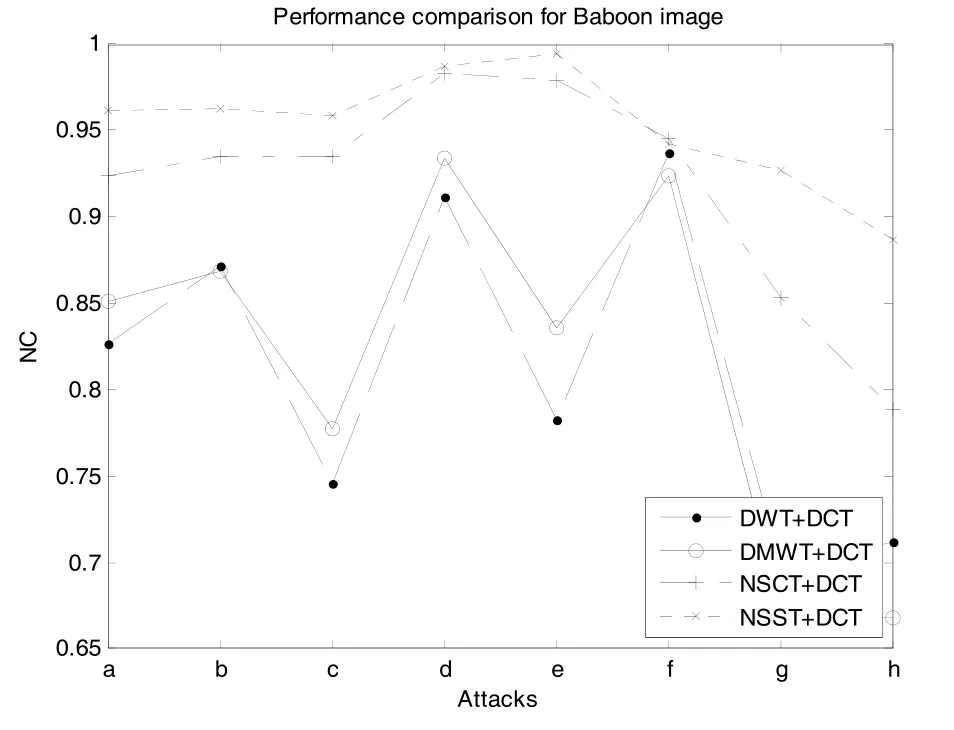
图5 Baboon图像下不同混合域算法性能比较
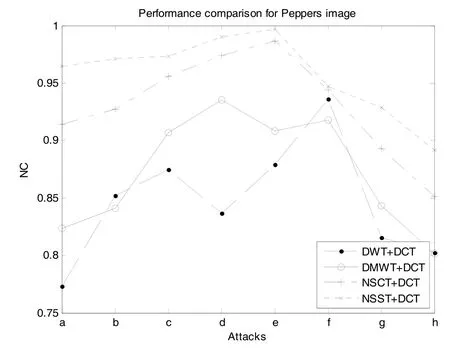
图6 Peppers图像下不同混合域算法性能比较
4 结 论
本文将NSST和DCT用于图像处理方面的优势有机结合,提出了一种新的基于子采样的混合域稳健零水印算法,用来进行数字图像的版权保护。空域中图像分块DCT变换后的DC系数之间存在一定的稳定性,这种稳定关系在NSST域中较其它变换域更为明显。利用这一特点,结合子采样和混沌映射技术构造零水印。实验结果表明,NSST+DCT零水印方案能够稳健地抵抗噪声、JPEG压缩和剪切等常见的攻击操作,具有一定的有效性和实际意义。同时,也说明了NSST应用于数字水印技术时相对于其它多尺度变换工具更具优越性,为数字水印研究提供了新的思路。
[1]李建忠. 抗几何攻击的鲁棒计算全息的零水印算法[J]. 光电工程, 2010, 37(8): 67-75.
[2]温 泉, 孙锬锋, 王树勋. 零水印的概念与应用[J].电子学报, 2003, 31(2): 214-216.
[3]Zhou Yaxun, Jin Wei. A novel image zero-watermarking scheme based on DWT-SVD [C]//Multimedia Technology 2011, 6002066: 2873-2876.
[4]Yang Weimin, Meng Lingmei. A zeros-watermarking algorithm based on chaotic system and DCT [C]//Asia-Pacific Computational Intelligence and Industrial Applications, 2009, 1: 71-74.
[5]Guo K, Labate D. Optimally sparse multidimensional representation using shearlets [J]. SIAM Journal on Mathematical Analysis, 2007, 39(1): 298-318.
[6]王 雷, 李 彬, 田联房. 基于平移不变剪切波变换的医学图像融合[J]. 华南理工大学学报(自然科学版), 2011, 39(12): 13-19.
[7]Miao Qiguang, Shi Cheng, Xu Pengfei, et al. A novel algorithm of image fusion using shearlets [J]. Optics Communications, 2011, 284(6): 1540-1547.
[8]Easley G R, Labate D, Colonna F. Shearlet-based total variation diffusion for denoising [J]. Image Processing,IEEE Transactions, 2009, 18(2): 260-268.
[9]Sheng Yi, Labate D, Easley G R, et al. A shearlet approach to edge analysis and detection [J]. Image Processing, IEEE Transactions, 2009, 18(5): 929-941.
[10]Easley G, Labate D, Lim W Q. Sparse directional image representations using the discrete shearlet transform [J]. Applied and Computational Harmonic Analysis, 2008, 25(1): 25-46.
