AR模型的功率谱估计方法及在故障检测中的应用
2013-03-20姚志飞姜万录朱勇
姚志飞,姜万录,朱勇
(1.河北广播电视大学,河北石家庄050090;2.燕山大学,河北秦皇岛066004)
干式真空泵目前主要应用于航天及航天卫星器件的地面性能测试系统、科学研究机构及高等院校实验室的真空获得设备、化学工业、生物及化学制药、光学器件过程工艺、半导体器件工艺制造、液晶生产、蚀刻和镀膜等行业中。随着真空应用领域的不断发展和真空应用要求的提高,传统的油润滑真空设备已经越来越不能够满足市场的苛刻要求。因此,出现了各种不同类型的干式真空泵,以满足市场上需要的无油洁净真空的要求。随之而来的对干式真空泵的故障检测也成为亟需解决的问题。
目前,在滚动轴承的故障诊断中,通常采用将振动信号进行基于Fourier 变换的经典谱分析方法,并从中提取故障特征信息,再进一步判断轴承的工作状态。但经典谱估计存在缺陷:(1)弱信号被强信号的旁瓣所淹没;(2)频率分辨率约为数据长度的倒数,导致分辨率不高;(3)频谱存有旁瓣,导致出现“泄漏”现象而使主瓣失真。虽然,之后出现了几种改进算法改善了谱估计的性能,但仍未能有效地克服上述缺点[1]。
现代谱分析方法利用被窗函数截取的有限信号以外的信息进行预测或外推,从而避免了功率泄漏,提高了分辨率。其中,参数模型法是较为常用、有效的方法,而有理参数模型中最成熟和常用的是AR模型[2]。作者将其应用于干式真空泵的滚动轴承故障检测,以设有内圈故障缺陷的滚动轴承振动信号为例进行验证,取得了较好的诊断结果。
1 AR模型及AR 功率谱
AR模型即自回归模型,该模型的当前输出是当前输入和过去输出的加权和,可用如下差分方程来表示:
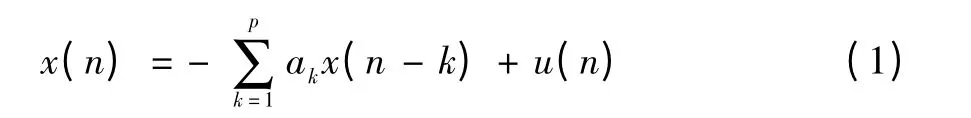
其中:ak(k=1,2,…,p)为AR模型的参数;p为AR模型阶数;u(n)为均值为零、方差为σ2的平稳白噪声序列。
由上式所定义的AR(p)过程{x(n)}可以看作是白噪声序列u(n)通过一个传递函数为

的全极点滤波器所产生,因此{x(n)}的功率谱密度px(ejω)可表示为:

从上式可以看出,只要求得参数ak(k=1,2,…,p)和σ2即可估计出{x(n)}的功率谱密度。
2 AR模型参数估计及最佳阶次选择
建模的关键是把模型的阶数和参数全部估计出来。AR参数估计的常用方法有:Yule-Walker或自相关法、最小二乘法、Burg算法等。作者采用计算简单、处理速度快、精度高的Yule-Walker方法,然后用Levinson-Durbin 递归算法计算AR模型系数[3]。
Yule-Walker方法主要基于一组被称为Yule-Walker方程的线性方程,它是联系自相关序列和AR模型参数的方程。可以通过计算含p+1阶自相关系数的Yule-Walker方程,计算p+1阶模型参数。
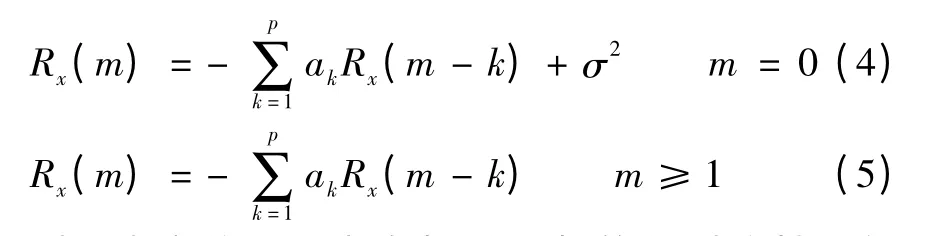
对于真实信号,由自相关函数的偶对称性可知Rx(m)=Rx(-m)。上式可写成矩阵形式:
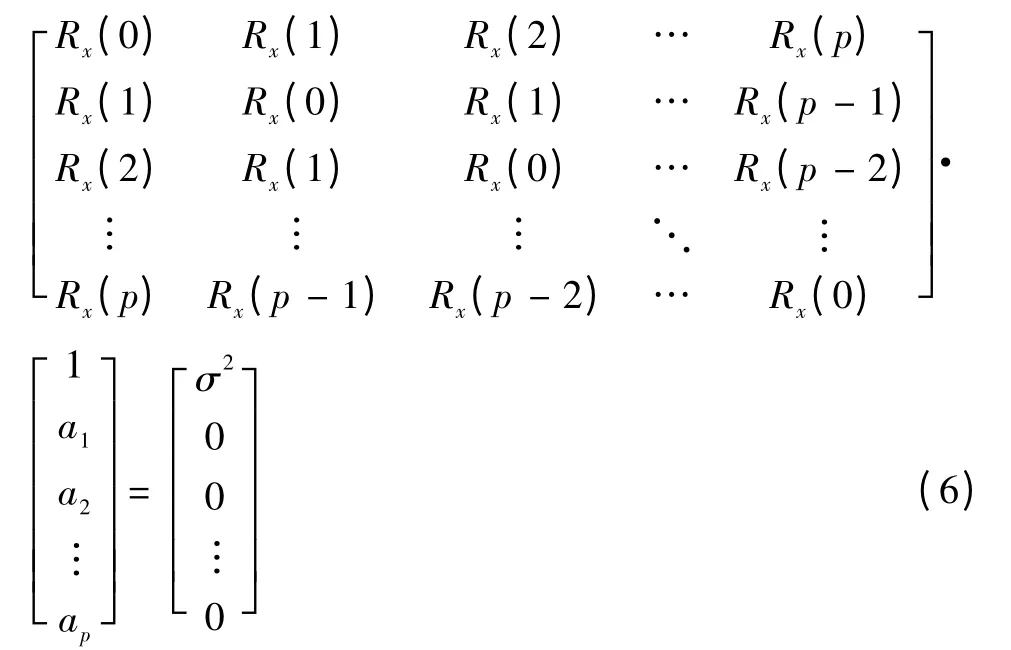
在AR 谱估计中,模型阶次的选择是一个关键问题。阶次太低将会导致过于平滑的谱估计结果,频率分辨率过低;而阶次太高,将会产生虚假谱峰,并且估计的方差也会增大。文中采用最终预测误差准则(FPE)判断最优阶次。该准则的计算公式为:
其中:N为数据点数;p为待估计参数,对AR(n)模型,p=n;为模型残差。
a 开始随着p的增大而减小,但当p 超过序列的真正模型阶数p0之后,值不再减少,这时将起着主导作用。因此,使FPE(p)取最小值的那个p 就可以判定为模型的最佳阶次,即
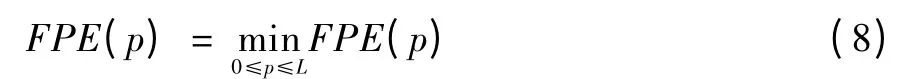
其中:L为预先设定的模型阶次上界。在阶次上界范围内,FPE 会存在若干个极小值,其中最小值对应的阶次为FPE 判阶准则给出的最佳阶次。显然,这样确定的最佳阶次与定阶上界有关,如果定阶上界选得过小,所得最合适阶次将会偏低;如果定阶上界选得过大,将加大计算量。因此,阶次上界的确定非常重要。目前人们只给出了样本长度N 在20~200之间的AR模型阶次确定的经验准则(即定阶上界)[4],但这并不适用于滚动轴承振动信号。文献[5]指出,估计阶次的上界L与样本长度N之间的关系为:但文中既没有给出理论推导,也没有给出实际验证。文献[6]通过实验研究表明,将样本长度的均方根值作为滚动轴承AR模型的定阶上界,可以得出满意的AR模型分析结果。
参数估计是在给定阶次的情况下进行的。由于事先无法判断模型的阶次,因此在建模过程中先给定模型的阶次,然后按照Yule-Walker法估计出AR模型的参数,得到相应阶次模型,最后取FPE(p)值最小的阶次作为模型的最佳阶次,同时也确定了AR模型。
3 AR模型分析在干式真空泵故障检测中的应用
滚动轴承常见的故障形式有内、外圈滚动面及滚动体表面的划痕、剥落、磕伤,以及保持架的断裂等。文中以干式真空泵滚动轴承内圈故障的振动信号为例进行AR 建模,并估计了其AR 谱,进行故障分析。在轴承外圈固定的情况下,滚动轴承内圈故障特征频率[7]:

其中:fr为内圈的旋转频率,D为轴承节径,d为滚动体直径,α为接触角,z为滚动体个数。已知试验中fr=105 Hz,D=46.2 mm,d=9.525 mm,z=9,α=24.97°,代入式(9)可求得fi=550 Hz。
实验采用的干式真空泵为5级罗茨+爪型干式真空泵,泵体结构示意图如图1所示。泵的每个转子都由固定于高、低真空端的一对单列深沟陶瓷轴承来固定。泵入口压力为2 kPa,轴转动频率为105 Hz。振动传感器ADXL105 (ADXL-HV)和BK4370V (BKHV)被安装在干式真空泵高真空端,另一只振动传感器ADXL105 (ADXL-LV)被安装在干式真空泵低真空端。振动信号由采样频率为40 Hz的数据采集卡采集,通过A/D转换器得到数字信号。振动加速度传感器的采样点数为80 000[8]。
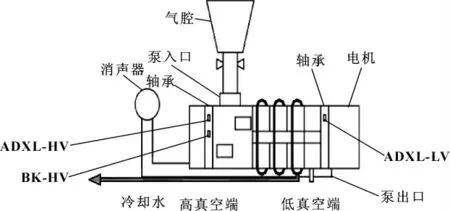
图1 干式真空泵结构示意图
实验中,采用3种测试工况:正常运行的泵1 和泵2,引入轴承故障的泵1。
在一定的气体负载范围内 (入口压力0~100 kPa),选用加速度传感器ADXL-HV 采集正常泵1 高真空端的无故障振动信号,得到基于AR模型的功率谱图,如图2所示。可以看出,无故障振动信号的典型的频谱含有谐波振动信号及其倍频的谱峰。采集真空泵有故障时振动信号,得到基于AR模型的功率谱,如图3所示。当在一个轴承上引入故障以后,其频谱就会有显著的差别,出现了频率为550 Hz的频峰。
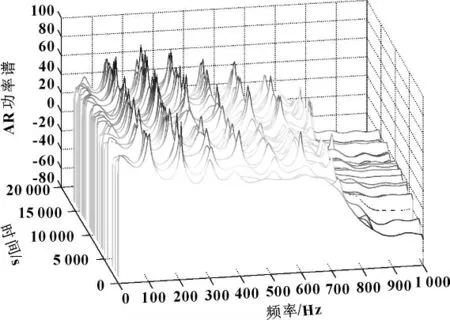
图2 不同入口压力时无故障振动信号的功率谱图

图3 不同入口压力时故障振动信号的功率谱图
为了对比有无故障的频谱图,作者将以上两个三维图叠加形成二维图,如图4所示。可知:故障特征频率大约为550 Hz,可初步判定为轴承内环故障。
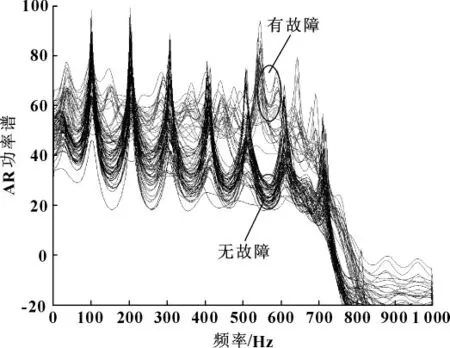
图4 ADXL-HV 捕获的有故障与无故障功率谱的对比图
同理,采用加速度传感器ADXL-LV 采集3种工况的低真空端振动信号分析得到功率谱图,叠加后的二维谱图如图5所示。用加速度传感器BK-HV 采集3种工况的高真空端的振动信号并作出其功率谱图,叠加后的二维谱图如图6所示。
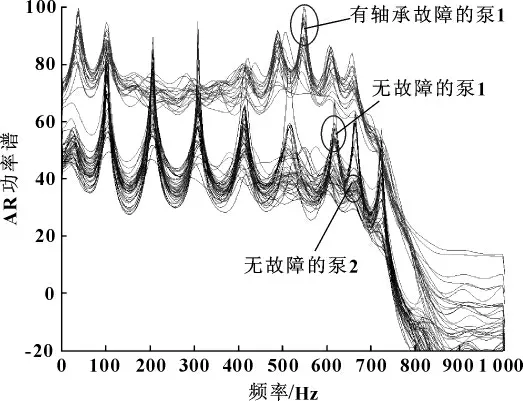
图5 ADXL-LV 捕获的有故障与无故障功率谱的对比图
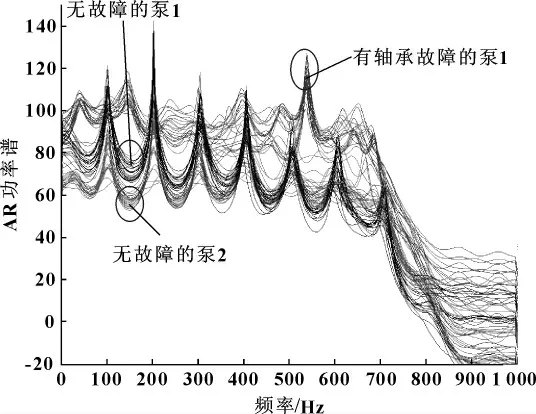
图6 BK-HV 捕获的有故障与无故障功率谱的对比图
对比3种工况振动信号的基于AR模型的功率谱,其故障特征频率都明显出现在550 Hz处。因此,可以进一步判断故障形式为轴承内环故障,这同试验所设定的故障形式吻合。
4 结论
对干式真空泵的滚动轴承故障进行了研究,分析了AR模型最佳参数选择原则,并运用AR 功率谱分析方法对泵实验数据进行了分析。实验研究结果表明:基于AR模型的功率谱分析方法对于干式真空泵的故障检测是有效的,为干式真空泵故障诊断的研究提供了一种可靠的方法。
【1】陆传赉.现代信号处理导论[M].北京:北京邮电大学出版社,2002.
【2】胡广书.数字信号处理[M].北京:清华大学出版社,2002.
【3】姚志飞.AR模型最佳阶次选择及其在故障检测中的应用研究[D].秦皇岛:燕山大学,2008.
【4】杨叔子,吴雅.时间序列分析的工程应用[M].武汉:华中理工大学出版社,1994.
【5】沈凤麟,叶中付,钱玉美.信号统计分析与处理[M].合肥:中国科学技术大学出版社,2002.
【6】赵联春,马家驹,范树迁,等.滚动轴承振动分析中的AR模型研究[J].中国机械工程,2004(3):210-213.
【7】张晨罡,郝伟.基于AR模型的滚动轴承故障检测[J].现代制造技术与设备,2006(5):35-40.
【8】JIANG W,SPURGEON S K,TWIDDLE J A,et al.A Wavelet Cluster-based Band-pass Filtering and Envelope Demodulation Approach with Application to Fault Diagnosis in a Dry Vacuum Pump[C]//Proceedings of the Institution of Mechanical Engineers:Part C,2007:1279-1286.
