基于李雅普诺夫稳定性的PID控制器参数整定与应用比较
2013-03-20曹淼龙李强
曹淼龙,李强
(浙江科技学院机械与汽车工程学院,浙江杭州310023)
PID控制器[1]是根据系统的输出输入误差,利用比例、积分、微分计算出控制量,具有结构简单,算法易实现、鲁棒性好、适应性强及可靠性高等优点,在控制工程领域应用非常广泛。
PID控制器的比例项减少对干扰的误差响应,积分项消除稳态误差,微分项则抑制动态响应。自Ziegler 和Nichols 提出PID参数整定方法[2]起,国内外学者及研究机构关于此问题的研究此起彼伏,如基于相幅裕度PID控制[3]、模糊自适应PID控制[4]、鲁棒PID控制[5]方法等。PID控制器参数整定要满足闭环系统得到预期响应的前提下,亦要提高系统稳定性,
近年来PID参数稳定域的研究越来越受到重视。文献[6]基于广义Hermite-Biehler 定理提出完整的PID参数稳定域,对非时滞对象进行H∞鲁棒设计;文献[7]基于Nyquist 稳定性判据解决PID控制器参数稳定域的计算。作者针对单输入-单输出(SISO)闭环反馈控制系统,基于李雅普诺夫稳定性原理,通过对比传统的Z-N 等整定方法,给出一种较为简单实用且易推广可行的PID控制器参数整定方法。
1 问题的描述
图1为典型的SISO 闭环反馈控制系统的基本结构图[8],其中,r、y分别为设定的参考值输入和控制对象输出,e为信号偏差量,d为干扰信号,u为控制信号,GK(s)和G(s)分别为PID控制器和控制对象。

图1 反馈控制系统的结构图
控制对象的传递函数G(s)设为:

式中:s为复变量,n≥m,an≠0;bm≠0,ai和bj均为已知数;i=0,1,…,n;j=0,1,…,m。
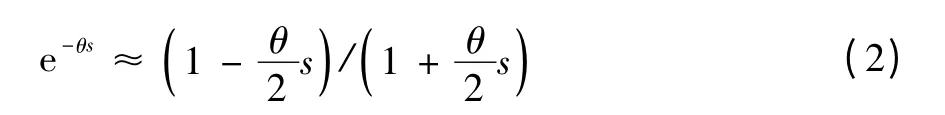
式中:θ为对象时滞。
PID控制器的传递函数GK(s)如下:
式中:kp、ki和kd分别为比例、积分和微分增益。
由控制对象G(s)与PID控制器GK(s)构成的负反馈闭环系统传递函数为:

若GP(s)已知,可通过根轨迹法考察系统的稳定性,判定系统是否稳定或是否符合设计的性能要求。
2 基于李雅普诺夫稳定性的PID参数的计算方法
把s=jω 代入公式(4),其中ω为信号频率,可得频率特性GP(jω),令幅频特性|GP(jω)|=1:
武陵自然村调查地面塌陷共37处,主要集中发生在2017年10月16~17日(矿洞透水发生于2017年10月14日),数量达34处,占调查总数的92%,仅有3处发生在11月20日。塌陷发生期间均有降雨过程。可见矿洞开采透水是本次塌陷发生的诱因,塌陷发生后,受降雨影响,塌陷点的规模逐渐扩大并伴随新的塌陷点出现。
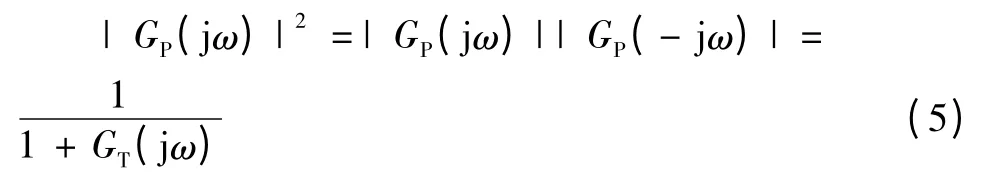
式中:

δr和δi分别表示GT(jω)的实部和虚部。由李雅普诺夫系统稳定性原理,为使系统稳定,特征方程的全部根,都是负实数或实部为负的复数,位于复数平面的左半平面,要保证闭环系统稳定,即δr=0。
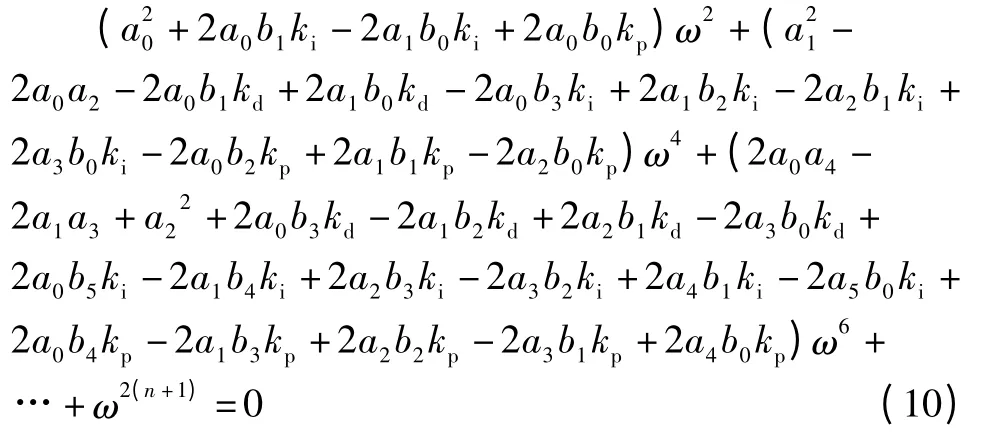
针对最小相角系统,用GT(jω)曲线对 (-1,j0)点的接近程度来表示系统的相对稳定性[9]。当ω趋向于0时,由公式(10)联列3个方程组即可求出PID控制器kp、ki和kd3个参数值。

3 仿真实例
3.1 典型的工业时滞过程应用
在工业过程控制中,大多数的控制对象都具有一阶惯性加纯时滞过程的动态特性[10],因而控制对象传递函数G(s)可以表示为:

式中:k为静态增益,τ为时间常数。
由公式(11)—(13)经计算,kp、ki和kd3个参数值如下:

文献[10]采用遗传算法求解鲁棒PID控制器的计算公式为:

例1,考虑一阶延迟过程[10]:

该对象PID控制器3种整定方法的结果如表1所示。

方法 kp ki k d Z-N[2]2.285 2.673 0.488 IAE-GA[10] 2.219 1 1.982 2 0.437 9文中方法1.25 2 0.5
在t=1 s 和t=15 s时分别加入单位阶跃输入和单位反向阶跃干扰信号,y(t)为系统输出,得到的系统响应如图2所示。
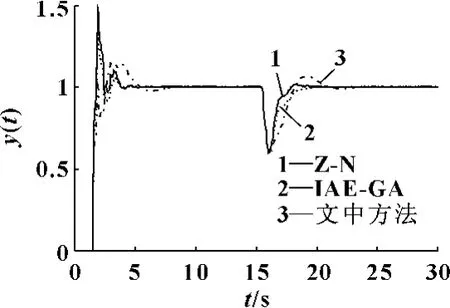
图2 例1的闭环仿真输出响应
从图2可以看出:Z-N方法和文献[8]的IAE-GA方法在前期时域跟踪性表现较差,超调量分别为47%左右和28%左右,在稳态值的±2%误差范围内调节时间分别为3.6 s 和2.9 s,但后期具有良好的时域抗干扰性,超调量分别为5.1%和2.3%;而文中方法有一定的折衷性,前期超调量为16%左右,调节时间为4.8 s,但后期超调量稍大,为9%,由此表现出优良的跟踪性和一定的抗干扰性。
3.2 机电控制工程的应用
机电控制工程常见的传递函数为:

文献[11]应用H∞控制理论派生出的闭环增益成形方法,设计鲁棒控制器计算公式为:
kp=ωca1ki=ωca0kd=ωca2
式中:ωc为闭环系统的截止频率。
由公式(11)—(13)经计算,kp、ki和kd3个参数值如下:

例2,永磁同步直线电机的传递函数[11]为:
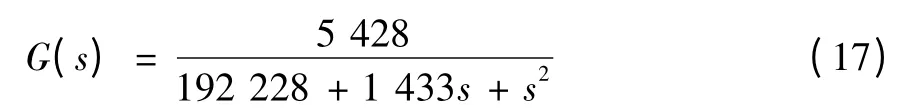
表2为该对象PID控制器两种整定方法的结果,经计算文献[11]的ωc取0.666 4 rad/s。
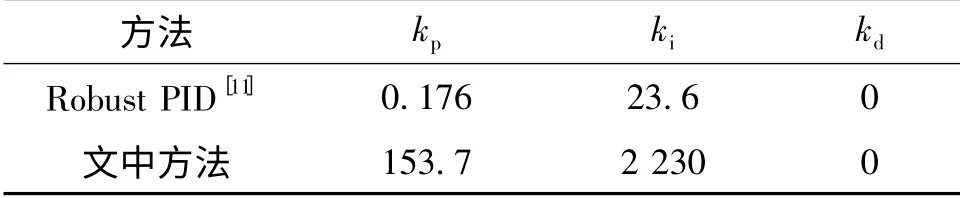
表2 永磁同步直线电机模型PID参数整定比较
在t=1 s 和t=15 s时分别加入单位阶跃输入和单位反向阶跃干扰信号,y(t)为系统输出,所得到的系统响应如图3所示。
从图3可以看出:文献[9]的鲁棒PID控制器跟踪性和抗干扰性均表现不佳,延迟时间达到4.6 s,后期的超调量为3.1%;而文中方法的时域跟踪性和抗干扰性都表现得较好,具有良好的鲁棒性能。

图3 例2的闭环仿真输出响应
4 结论
文中基于根轨迹法确定满足闭环反馈控制系统稳定性要求的目标方程组;然后在李雅普诺夫稳定性判据基础上,推导PID控制器参数整定的计算方法,分别对具有代表性的工业工程——一阶迟延过程的近似模型和永磁同步直线电机模型进行跟踪性和抗干扰性仿真分析和比较。仿真分析结果表明:采用该方法设计的PID控制器在保证闭环系统稳定性的前提下,能获得较好的跟踪性和抗干扰性。简化控制系统的传递函数后无需类似Z-N 作根轨迹或伯特图等来确定控制参数,只需通过对闭环系统函数分解并近似后推导出相应的方程组求出控制器参数值。该方法主要优点是参数计算程序化,便捷可行易推广,适用于各类时滞对象或非时滞对象的鲁棒控制,但同时若函数的阶数较多,求解方程组复杂,计算工作量较大,通常需借助计算机来完成。
【1】ASTROM K J,HAGGLUND T.PID Controllers:Theory,Design and Tuning[M].2nd Edition.Research Triangle Park,NC:Instrument Society of America,1995.
【2】ZIEGLER J G,NICHOLS N B.Optimum Settings for Automatic Controllers[J].Transactions of the American Society of Mechanical Engineers,1942,64(8):759-768.
【3】LEE C H.A Survey of PID Controller Design Based on Gain and Phase Margins[J].International Journal of Computational Cognition,2004,2(3):63-100.
【4】HOOSHMANDI K,YAZDIZADEH A,MONTAZERI,M.Cascade Adaptive Predictive Controller Design Based on Multiple Models(Case study:GILAN Combined Cycle)[C]//2009 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Singapore,2009:1964-1969.
【5】TOSCANO R.A Simple Robust PI/PID Controller Design via Numerical Optimization Approach[J].Journal of Process Control,2005,15(1):81-88.
【6】SILVA G J,DATTA A,BHATTACHARYYA S P.New Results on the Synthesis of PID Controllers[J].IEEE Transactions on Automatic Control,2002,47(2):241-252.
【7】MARTELLI G.Comments on“New Results on the Synthesis of PID Controllers”[J].IEEE Transactions on Automatic Control,2005,50(9):1468-1469.
【8】欧林林,顾诞英,张卫东.基于幅值裕度和相位裕度的PID参数最优整定方法[J].控制理论与应用,2007,24(5):837-940.
【9】KUANG S,CONG S.Lyapunov Control Methods of Closed Quantum Systems [J].Automatica(Journal of IFAC),2008,44(1):98-108.
【10】金鑫,谭文,李志军,等.典型工业过程鲁棒PID控制器的整定[J].控制理论与应用,2005,22 (6):947-953.
【11】潘霞远,刘希喆,吴捷,等.永磁同步直线电机的鲁棒PID控制[J].电机与控制应用,2008,35(9):34-38,65.
