冷发射实验台的模糊自适应串级控制仿真研究

韩洋洋，马大为，乐贵高，胡健，孙德

(南京理工大学机械工程学院，江苏南京210094)

在冷发射系统中，导弹在发射过程中的弹射力会造成车体的震动进而影响导弹发射精度，实际工作过程中要求发射车在受到导弹弹射力作用后能够快速稳定地恢复到稳定位置。文中主要通过液压试验平台模拟发射车受到冲击载荷的震动特性，该试验平台是由4个非对称液压缸共同支撑，每个液压缸上装有位移/速度传感器。由于控制阀的压力流量不确定性和非对称液压缸的往复运动，使得阀控液压缸本身是一个非线性系统。经典PID控制自诞生以来由于结构简单、运算量小被广泛应用于各种工业控制领域，但是其缺点是系统抗外部扰动和控制非线性系统能力较差。模糊控制是人工智能控制的一种，可以有效利用先前控制经验并将其转化为推理逻辑，但是单独模糊控制器的缺点是控制精度低。文献[1]将模糊控制和PID 调节相结合，根据误差实时变化，利用模糊规则调整PID参数，建立模糊自整定PID控制系统，但该控制系统仅为单回路控制系统，抗扰动能力不够强。文献[2－3]将模糊控制与PID控制相结合，建立了模糊PID 串级控制系统，内回路为PID控制器，外回路为模糊控制器。文献[2]基于非线性归一模糊量化方法给出了带修正函数模糊规则自调整的控制方法，由于位置环仅采用模糊控制，系统稳态误差比较大，从文献给出的结果图可以看出阶跃响应出现抖动;文献[3]中内回路仅采用比例控制，外回路采用模糊控制器输出Kp、Ki、Kd3个参数。由于内回路仅采用比例控制，系统上升时间较长，会产生超调和稳态误差。

文中针对实验台的特点，取实验台的一个液压缸支腿，建立其模糊PID 自适应串级控制模型，内回路(速度环)采用经典的PID控制器，外回路(位置环)采用增量式模糊自适应PID控制器，即利用模糊控制器输出PID参数变化量ΔKp、ΔKi、。

1 实验台液压缸支腿控制模型

图1 液压缸串级控制方框图

结合文献[4－6]得到液压缸串级控制系统的方框图，如图1。图中:ωh为阀控液压缸系统谐振频率;ωf为伺服阀谐振频率;ζh为阀控液压缸系统阻尼比;ζf为伺服阀阻尼比;Kq为阀控液压缸系统增益;K为伺服阀增益;Km为扰动外力微分系数;Kn为扰动外力增益;Kpx、Kix、Kdx分别为位置环比例、积分、微分系数;Kpv、Kiv、Kdv分别为速度环比例、积分、微分系数;T为滤波器时间常数。

文中采用对称伺服阀控制非对称液压缸，这种控制方式在液压缸换向时会产生很大的压力跳动，使系统产生震动且液压缸传递函数随活塞杆运动方向变化而变化，使系统会表现出动态不对称性[6]。

当仅仅采用位置PID控制器时，即将内部速度环去掉，液压缸输出位移与扰动力之间的传递函数为:

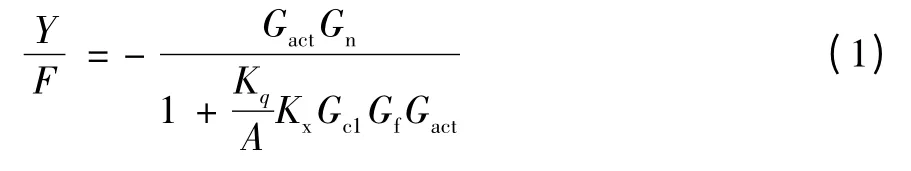
令

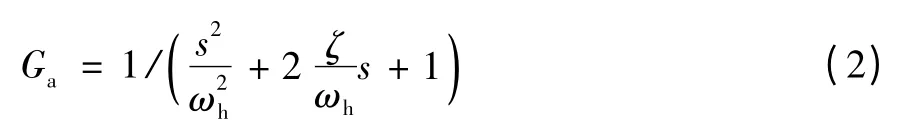
当采用串级控制时，液压缸位移与扰动力之间的传递函数为

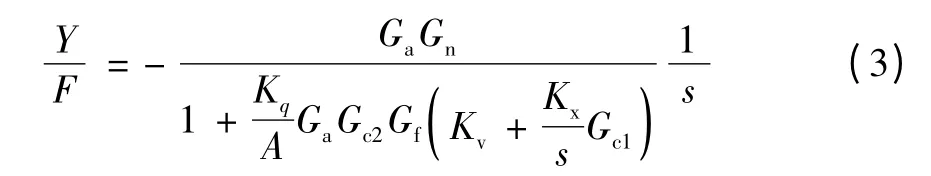
由于

式(2)化简后为

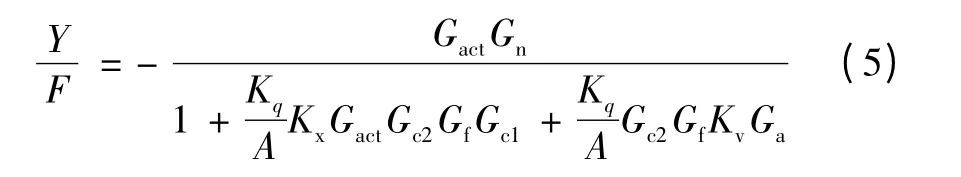
结合式(1)、(5)知，两式分子是相同的，分母式(5)比式(1)多了一项KqKvGc2GfGa/A，而且式(5)的分母第二项比式(1)的分母的第二项大得多。因此，由于内环控制的存在，系统对干扰的抑制能力变强，当其他参数不变时，内环的增益越大系统抑制干扰能力越强。

2 模糊自适应串级控制器设计

文中位置环采用二维模糊控制器，将位置误差与误差变化率输入模糊控制器，通过模糊推理机计算，输出PID参数的修正量，即ΔKp、ΔKi、ΔKd。

位置环自适应控制器控制算法为:

模糊控制器是系统实现自适应控制的核心，在设计模糊控制器时的主要原则是:当位置误差较大时，应该增大ΔKp，以提高系统的响应速度，ΔKi取较小值，以减小系统的超调量;当位置误差较小时，应当减小ΔKp，适当增大ΔKi，以便减小稳态误差。ΔKd抑制控制量的变化，是对ΔKp、ΔKi的补偿。具体的模糊规则如表1[7－8]。

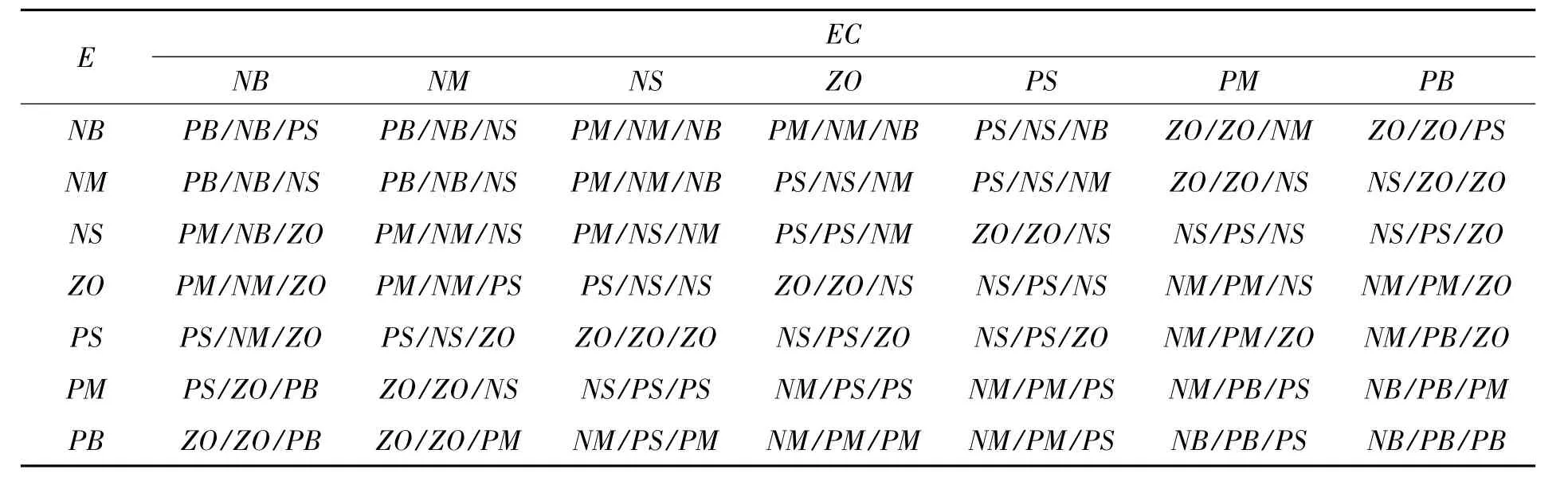
E EC NB NM NS ZO PS PM PB NB PB/NB/PS PB/NB/NS PM/NM/NB PM/NM/NB PS/NS /NB ZO/ZO/NM ZO/ZO/PS NM PB/NB/NS PB/NB/NS PM/NM/NB PS/NS/NM PS/NS/NM ZO/ZO/NS NS/ZO/ZO NS PM/NB/ZO PM/NM/NS PM/NS/NM PS/PS/NM ZO/ZO/NS NS/PS/NS NS/PS/ZO ZO PM/NM/ZO PM/NM/PS PS/NS/NS ZO/ZO/NS NS/PS/NS NM/PM/NS NM/PM/ZO PS PS/NM/ZO PS/NS/ZO ZO/ZO/ZO NS/PS/ZO NS/PS/ZO NM/PM/ZO NM/PB/ZO PM PS/ZO/PB ZO/ZO/NS NS/PS/PS NM/PS/PS NM/PM/PS NM/PB/PS NB/PB/PM PB ZO/ZO/PB ZO/ZO/PM NM/PS/PM NM/PM/PM NM/PM/PS NB/PB/PS NB/PB/PB

3 系统仿真与结果

3.1 仿真模型建立

仿真模型建立AMESim与Simlink仿真模型如图2和图3所示。

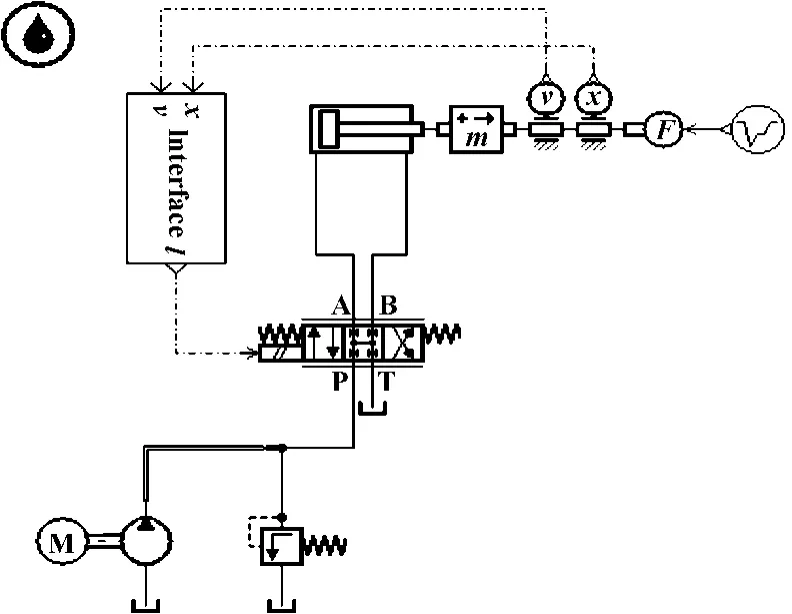
图2 模糊自适应串级控制液压系统模型

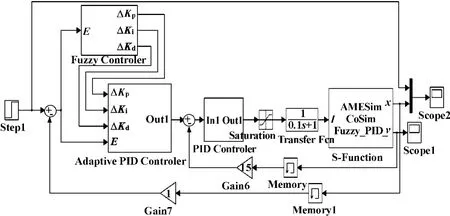
图3 模糊自适应串级控制Simulink 控制系统模型

模型的主要参数如下:液压缸缸径125 mm，杆径70 mm，行程0.5 m;溢流阀的压力设定为25 MPa，伺服阀额定流量54 L/min，额定供油压力21 MPa;位置参考信号为阶跃信号，幅值为0.4 m，干扰力为持续1 s、幅值为100 kN的冲击力。

在Simulink 中建立如下的联合仿真模型，控制信号输入伺服阀前要经过限幅环节和滤波器。速度环的PID参数为Kp=20，Ki=1×10－6，Kd=1×10－3;位置环的PID参数为10－3。

3.2 系统仿真分析

系统参考信号为幅值为0.4 m的阶跃信号，在t=7 s时刻突然施加载荷为100 kN的冲击力，持续时间为1 s，仿真结果如下所示。

模糊自适应串级PID控制和单回路PID控制阶跃响应仿真曲线分别见图4和5。模糊自适应串级PID参数整定曲线见图6和7。

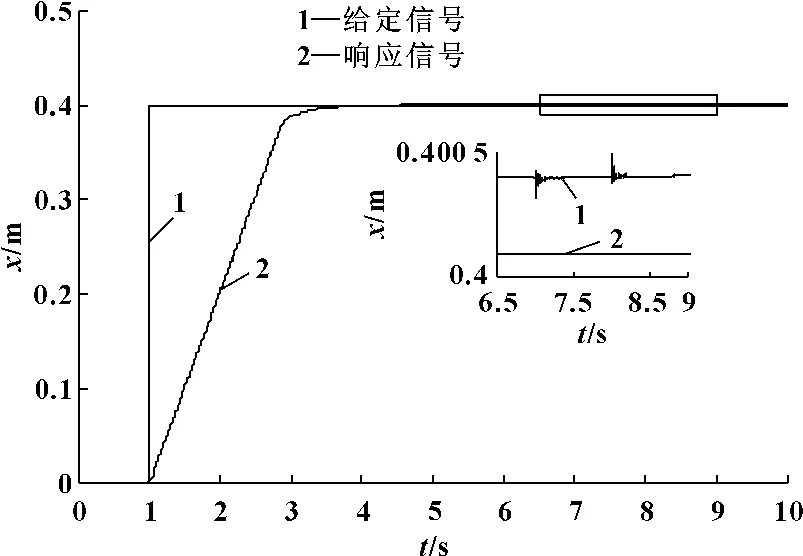
图4 模糊自适应串级控制阶跃响应曲线

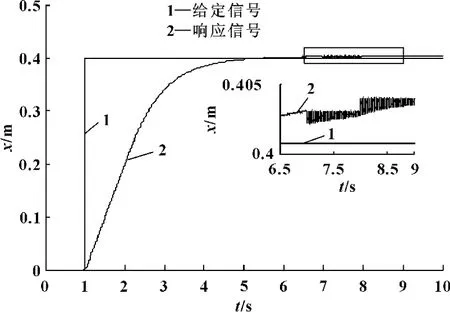
图5 单回路PID 控制阶跃响应曲线

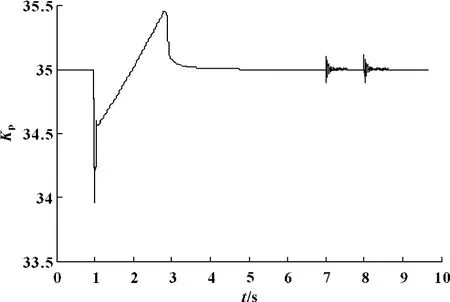
图6 Kp 整定曲线

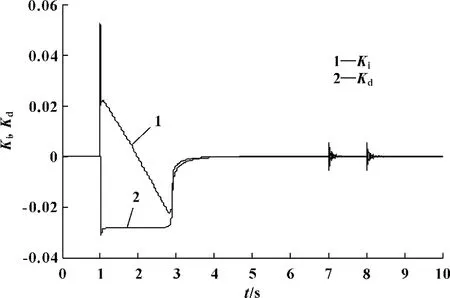
图7 Ki 和Kd 整定曲线

由图4和图5可以看出:实验台在单回路经典PID控制下，经冲击力作用后，震动幅度较大且衰减周期较长，而在模糊自适应串级控制下，由于系统的控制参数能够实时变化使系统的响应速度增快，系统震动幅值可以控制在非常小的范围之内，且系统可以很快恢复到稳定状态，并且液压缸上升速度比单回路经典PID控制下的快。由图6、图7看出:在液压缸上升阶段，位置环的Kp不断增大，Ki不断减小;在t=7 s 冲击力作用时，Kp、Ki，Kd不断自适应调节，以达到快速稳定实验台的目的。

4 总结

在控制液压缸时采用模糊自适应串级控制策略，建立了液压缸速度环和位置环双闭环控制模型，速度环采用经典的PID控制器，位置环采用模糊自适应PID控制器，利用模糊控制器在线实时调节PID的参数。仿真结果表明:在冲击载荷下，模糊自适应串级控制器相较于单回路传统PID控制器，能有效地减小系统的震荡时间和震荡幅度，增强系统鲁棒性。

【1】卢红影，姜继海，王頔.模糊自适应PID控制控制策略的液压变压器驱动直线负载系统研究[J].机床与液压，2009，37(9):58－61.

【2】丁国锋，王孙安，林延圻，等.模糊PID 串级控制在电液伺服系统中的应用[J].机床与液压，1996(2):10－11.

【3】王启志，王晓霞，王永初.一种自适应模糊串级控制仿真[J].计算机仿真，2003(3):65－67.

【4】刘长年.非对称伺服油缸的动态研究[J].机床与液压，1985(1):1－10.

【5】江玲玲，张俊俊.基于AMESim与Matlab/Simulink 联合仿真技术的接口与应用研究[J].机床与液压，2008，36(1):148－149.

【6】肖晟，强保民.基于对称四通阀控非对称液压缸的电液比例位置控制系统建模与仿真[J].机床与液压，2009，37(6):96－97.

【7】冯永宝，常钰.基于Fuzzy-PID控制的调平支腿精确定位的仿真研究[J].液压气动与密封，2011(19):19－22.

【8】凌轩，曹树平，朱玉泉，等.基于模糊自适应控制的四点支撑液压平台自动调平方法[J].机床与液压，2007，35(12):84－86.