基于MRFAC的液压双缸同步控制系统设计与仿真

沙郑辉，赵升吨

(西安交通大学机械工程学院，陕西西安710049)

模具研配压力机是汽车、塑料、压铸等工业中制造、精修大中型模具的关键设备之一。随着我国模具现代化科学技术的不断进步和发展，大多数模具制造企业已经完成了从人工锤击合模到模具研配压力机自动合模的转变，可是目前很少有国内研制的成型产品，绝大多数大中型企业修理模具的机械都为非国产(大陆地区)，如海南马自达模具车间的模具研配压力机是从台湾迪斯油压工业有限公司引进的，这样不仅大大提高了成本，而且模具的修理比较困难。而频频更换价值很高的模具是一种资金的浪费，因此高精度研配液压机的研制就显得比较迫切，具有很大的市场应用价值与潜力。而研配压力机的液压控制系统是保证压力机研配精度的关键。针对此问题，作者提出了基于模型参考模糊自适应(MRFAC)控制的液压双缸同步控制系统，并对其进行了仿真验证。

作者所设计的模具压力机的的基本设计参数如下表1所示。

表1 数控模具研配压力机的主要技术参数[1]

1 液压同步控制系统方案论证

1.1 典型液压同步控制回路

液压同步回路有很多，目前常见的主要可分为以下几种形式[2－3]:机械强制同步，流量同步回路，容积同步回路，电液伺服同步回路等。其中，最简单的是依靠横梁的刚度和小间隙、高平行度导轨的导向强制横梁平动;也可以利用齿轮—齿条或连杆等机构实现双缸同步。流量同步是通过流量控制阀控制流入或流出两液压缸的流量，使液压缸活塞运动速度相同，实现速度同步。图1(a)是采用调速阀和流向整流板使液压缸双向均能进行节流控制的同步回路，但系统效率低，同步误差在5%～10%左右。容积同步回路是两相等容积油液分配到尺寸相同的两液压缸，实现两液压缸位移同步，同步精度高，系统的效率也较高。图1(b)为带补油装置的串联缸同步回路，但是两串联油腔的泄漏会使两活塞产生位置误差，长期运动误差会不断积累起来，应采取措施使一个液压缸达到行程端点后，向串联油腔补油或由此排油，消除误差。电液伺服同步回路实际上也是一种流量控制回路，其关键元件是电液伺服阀。电液伺服阀具有体积小、结构紧凑、功率放大系数高、直线性好、死区小、灵敏度高、动态性能好、响应速度快、能实现连续准确地控制流量的作用等优点，因此在液压系统中得到了广泛的应用。由于采用电液伺服阀，必须用能产生电信号的位移传感器检测2个液压缸的位移，将2个传感信号比较得到位移偏差信号，再输入伺服阀进行流量控制，系统位置同步精度可达10－2级。此外还有利用同步缸直接构造同步回路等，这里不再一一赘述。

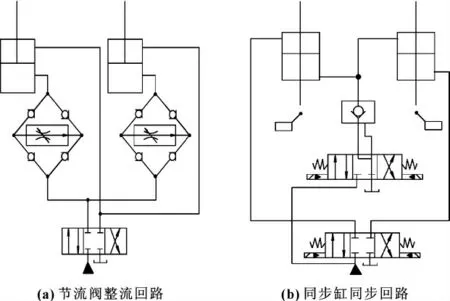
图1 常用液压缸同步回路［2］

1.2 新型数控模具研配压力机双缸同步控制系统

模具研配液压机的研配精度是通过安装在动梁上双液压缸的同步运行来实现的，但在实际中存在重心不对称，两负载的微小差别，液压回路流量、压力的波动，机械系统安装误差及运行后的累计误差等问题[4]。为了保证系统在下行过程中的同步精度，作者在综合比较上述几种同步方案，并结合该模具研配压力机设计精度要求，最终确定了文献[5]中所提出的比例流量阀与伺服阀同时控制的同步控制方案，即在主油路上采用双比例流量阀，并且在旁路采用伺服阀同时控制的双缸同步下行，工作原理图如图2所示。

图2 模具研配压力机同步系统原理

其控制原理可概括为两个步骤[5]:

(1)双缸下行过程中的粗略同步的实现。比例流量阀1接收位移指令信号，比例流量阀2同时接收速度信号及两液压缸位移的偏差信号，这样缸1为主动缸，缸2为从动缸，改变指令信号即可改变两缸的位移。信号由压力机控制系统主控制器 (如PLC)给出，电控器将其输入电压转换为两个比例阀的控制电流，控制阀的流量，从而控制缸的工作速度。通过光栅位移传感器L1、L2 测出缸即时位移，其输出值为电压VL1、VL2，VL1与VL2的差值反映了两缸同步误差，将其作为反馈电路输入，经放大作为系统负反馈叠加至系统输入端，从而即时修正位移，确保双缸的同步运行。其优点是:在闭环控制的情况下，只有一个比例流量阀起自动调节作用，另一个起固定节流的作用，因此相当于装了一个备用阀，这种余度设计提高了系统的可靠性。

(2)研配过程中精确同步的实现。由于比例阀存在死区及严重的流量非线性，尽管在双缸下行过程中可以保证一定程度的同步精度，可是在动梁与下梁合模的过程中应用比例流量阀无法满足模具研配的精度要求，因此在此甚础上，设计了一个伺服阀控制的双缸同步，从而使动梁与下梁精确合模定位，当达到上下模具合模的指定位置时，伺服阀开始工作，缸1为主动缸，位移传感器Ll、L2分别检测两缸的位置信号，将两位置信号进行比较，经放大电路放大后，输入到伺服阀中形成偏差信号，从而对缸2 进行补油或放油，直到两缸同步运行。此系统按输入的电流信号来控制液流的方向，亦为闭环控制。

2 液压元件数学建模及主动缸液压伺服系统设计

由上述分析可知，作者所设计的同步控制系统分为两个阶段，显然，研配过程的精确同步是作者更为关心的，关系到合模的精度，并最终影响模具研配的质量，需要重点分析与讨论。这一阶段中的控制元件为电液伺服阀，执行元件为液压缸，反馈元件为光栅位移传感器，如图3所示。因此，必须对这几个关键部件进行数学建模，以便对此阶段的控制系统进行分析。

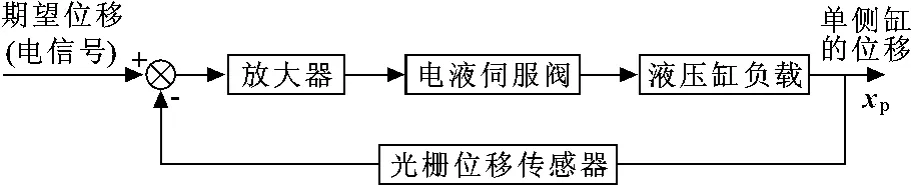
图3 主动缸电液伺服控制系统的方框图

(1)电液伺服阀的数学建模

文中所选用的电液伺服阀为力反馈式，第一级液压放大器为双喷嘴挡板阀，由永磁动铁式力矩马达控制;第二级(若为三级阀，则后两级)液压放大器为四通滑阀。在大多数电液伺服系统中，伺服阀的动态响应往往高于动力元件的动态响应。为了简化系统的动态特性分析与设计，伺服阀的传递函数可以简化，一般可用二阶振荡环节表示[6－7]。

二阶近似的传递函数可由下式估计:

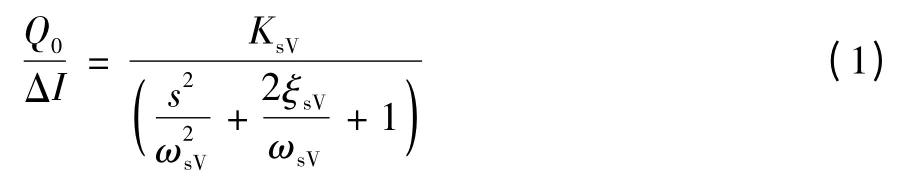
式中:KsV为伺服阀的流量增益;

ωsV为伺服阀固有频率;

ξsV为伺服阀阻尼比。

(2)阀控非对称液压缸的数学建模

在得出控制元件电液伺服阀的数学表达式后，作者对执行元件非对称液压缸进行数学建模。此外，通常情况下伺服系统的负载在很多情况下是以惯性负载为主，而没有弹性负载或弹性负载很小，可以忽略。假设在该系统中没有负载干扰力FL，则阀控非对称液压缸的传递函数可简化为[8]:

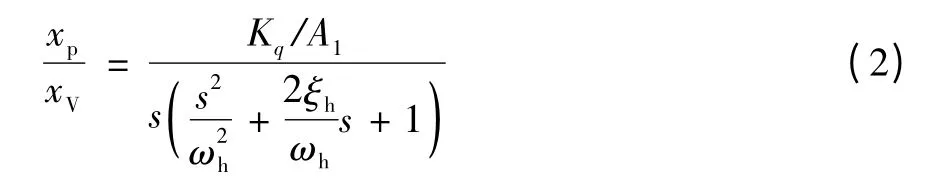
式中:xp为液压缸的位移(m);

xV为滑阀阀芯的位移(m);

Kq为滑阀的流量系数(m2/s);

A1为液压缸有杆腔的面积(m2);

ωh为液压阻尼固有频率;

ξh为液压阻尼比。

(3)位移传感器与放大器

一般位移传感器自身带有放大系数，根据设计参数确定具体型号后即可确定相应的比例系数Kf。

至此，作者得出了主动缸精确研配时电液伺服系统各环节传递函数的确切表达式。由表1中研配压力机的相关设计参数可以确定伺服阀、液压缸以及位移传感器的型号，从而确定计算参数。具体的选型和参数计算不在这里赘述。最终可确定方框图中系统的开环传递函数的具体表达式为:

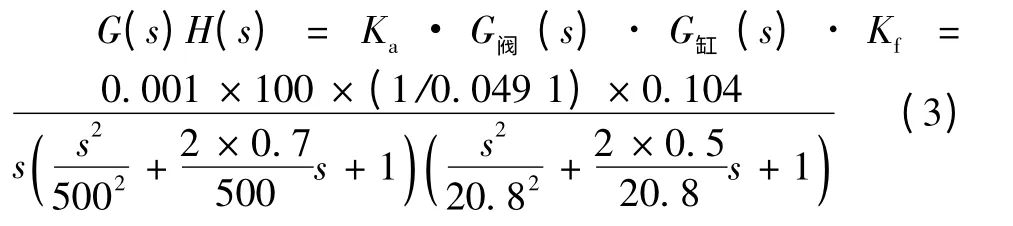
3 主缸伺服系统的时频分析及PID校正

3.1 系统的时频分析

根据上述计算数据，绘制Simulink仿真如图4所示。经计算，可得系统的单位阶跃响应如图5所示。同时可获得系统的频域特性曲线如图6所示。

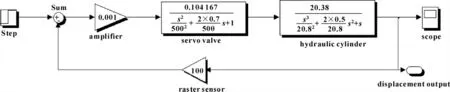
图4 主动缸液压伺服系统的Simulink 模型

由图5的单位阶跃响应可以看出:系统响应无超调，无震荡，达到稳态时间大约为28 s，可见系统的动态特性良好，但是达到稳态所用的时间太长。

图5 主动缸液压伺服系统阶跃仿真结果

系统的频域特征见图6，可见:系统的幅值裕度Kg=Gm=39.3 dB，相位裕度γ=Pm=89.4°，均为正值，根据系统稳定性判据，可知系统是稳定。同时，还可求得系统的频宽为W－3dB=14.5 rad/s，所以系统的响应速度较快。此系统与现有的实际系统进行比较，数据基本相符[9]，说明此数学建模能够通过验证。

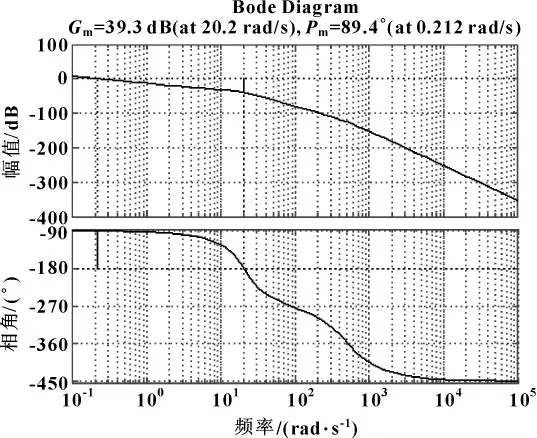
图6 主动缸液压伺服系统频域分析

3.2 主动缸电液伺服控制系统的PID校正

由上述分析可知，其单位阶跃响应达到稳态时间很慢，因而考虑对主缸伺服系统进行改进。考虑到该压力机电液伺服系统的双缸同步误差主要是由于从动缸的跟踪误差引起的，因此，在这里只对主动缸采用传统PID 进行校正，而不采用其他复杂控制算法，以提高整个系统的计算效率。

PID算法中的比例Kp、积分Ki和微分Kd系数的选取与整定，采用实验凑试的方法确定初始值。最终确定Kp=18，Ki=0.002，Kd=0.5，得仿真曲线如图7所示。

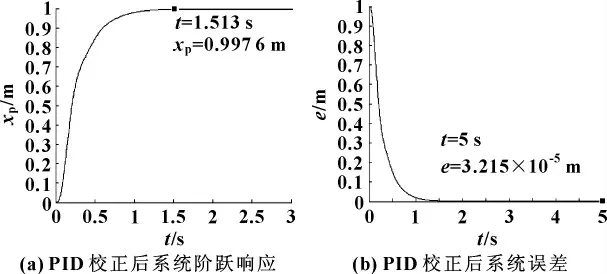
图7 主动缸电液伺服系统PID校正仿真图

由图7可以看出:加入PID的电液伺服系统时域动态特性较原系统有了明显改善，特别是达到稳态的时间由原先的28 s 缩短至1.5 s，大大提高了系统的响应速度，而且稳态误差仅为0.032 mm。至此，作者设计了主动缸的电液伺服系统，并对其进行了PID校正，为后面的双缸同步误差分析打下了坚实的基础。

4 双缸同步控制策略的分析和选择

4.1 同步控制策略初探

上一节，作者建立了研配压力机主动缸的液压伺服系统模型，而此模具研配压力机采用双缸同步控制系统方案，故这里对双缸同步控制系统进行数学建模，并对同步误差进行分析，并试图找到较合适的控制策略使压力机获得满意的研配精度。

在第1.2节中，已确定了比例流量阀与伺服阀同时控制的同步控制方案，但在具体进行同步控制时，有不同的控制策略，因此需要进行比较分析，从而选择适合该伺服系统的同步控制方法。目前，同步系统中较多采用“并联结构”和“串联结构”两种控制策略[10]，如图8(a)和(b)所示，文中忽略了执行元件1 和2之间的耦合环节。“并联结构”是指两个需同步控制的执行元件跟踪设定的理想输出而都分别受到控制并达到同步驱动。“串联结构”是指两个需同步控制的执行元件以其中一个的输出为理想输出，而另一个执行元件受到控制来跟踪这一选定的理想输出并达到同步驱动。

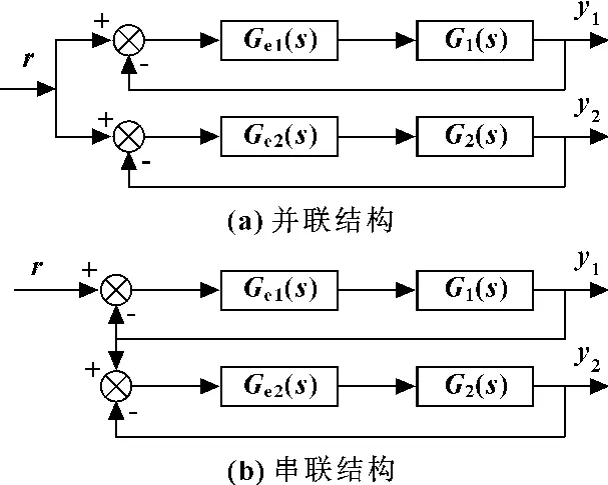
图8 同步控制策略

图8中控制环节Ge1(s)和Ge2(s)分别控制两只油缸的位移y1和y2跟随设定值，G1(s)和G2(s)为被控对象的传递函数。通常，位置同步系统的首要控制要求是稳态同步误差。另一方面，假设稳态同步误差已满足工程上的要求，但由于同步系统结构型式的不同，以及组成同步系统的各控制系统特性的差异等，系统仍会产生较大的动态同步误差，而当这种动态同步误差超过一定值时在工程上也是不允许的。因此要获得良好的位置同步控制系统，在保证稳态同步误差的基础上，还必须兼顾动态同步误差。因此，需对上述两种控制策略进行误差分析。

首先，被控对象的数学模型已在第2节推导，见式(3)。仿真时，为参照实际情况，被控对象的特征参数应设置不同值以模拟实际情况。运行仿真，结果如图9所示，其中y1和y2分别为缸1 和缸2的位移输出，e=y1－y2即为双缸同步误差。

由图9可看出:

(1)在图(a)中，由于组成同步系统的两个子系统的特征参数不同，采用“并联结构”会带来较大的动态同步误差，达到0.254 m。实际液压系统中参数是时变的，要保证在复杂工况下，两个子系统特征参数随时匹配就更困难，而且稳态误差也可能进一步加大，所以这种控制方式效果不佳。

(2)在图(b)中，由于从动缸的位移y2跟踪主动缸的y1具有延时性，从而产生了更大的动态同步误差，达到了0.417 m。此外，上述两种方式从动缸达到稳态的时间稍慢，均在2 s以后，从而使达到稳态同步误差的时间也随之延长，不利于同步精度的控制。

图9 两种同步控制策略的仿真结果

综上所述，组成同步系统的子系统中各元件的性能间很难具有严格的匹配关系，所以“并联结构”难以得到良好的控制性能。对于“串联结构”，因为从动系统的输出变量y2跟踪主动系统的输出y1具有延时性，所以系统在响应过程中会出现较大的动态同步误差。这两种结构均存在不同的缺陷，需设计新的同步控制系统方案。

4.2 基于模型参考思想的串并联复合同步控制

基于上述串联结构和并联结构的特点，借鉴模型参考自适应的原理和概念，提出了基于模型参考的串并联复合同步控制策略。

图10 模型参考自适应控制原理图

模型参考自适应控制(MRAC)是自适应控制中的一类[11]。通常包括4个部分:参考模型、被控对象、常规反馈控制器和自适应控制律，如图10所示。

图10中参考模型的输出Ym代表系统希望的动态响应，也就是用理想模型的输出来表示对系统的性能要求。当被控对象由于外界环境或工作状态的改变使其运行特性偏离了最优轨线时，被控对象的输出Y与理想模型的输出Ym相比较，产生广义误差e。e 通过自适应机构，根据自适应规律产生反馈去修正调节器的参数，或产生一个附加的输入信号作用于可调系统，使可调系统的输出Y与参考模型的输出相一致，使e 趋于零。

作者根据上述模型参考的控制机制，将缸1的数学模型视为缸2的参考模型，这样缸2的输出就会最大化地与缸1的输出相一致，从而使同步误差e 趋于零。可见，从理论上讲，将模型参考的概念应用于双缸电液伺服控制系统应该会有非常好的同步控制效果。由于缸2 同时接收位移信号和缸1的输出信号，所以整个系统从结构上讲，又是一个串并联复合控制。其同步控制原理图如图11所示。

图11 基于模型参考的串并联复合同步

用Simulink 对控制方案进行仿真实验，得实验结果如图12所示。

图12 基于模型参考的串并联复合同步控制仿真

从图12可以明显看出:尽管两个子系统的特征参数不同，但系统在“并联结构”的基础上增加了对参考模型缸1的同步误差调节器，使y2可迅速跟踪设定值和y1的变化，最大动态误差仅为0.21 m，双缸运行基本同步，因此获得了较为满意的动态同步误差。但是，从图12 中依然可以看出，在系统运行的初始阶段，缸2的输出略微超调，使得这部分的动态同步误差略大，这主要是由于传统PID算法参数一旦给定，无法根据被控对象的运行状况进行在线调节，因此应寻找合适的控制算法来尽量消除这一部分动态同步误差。

5 MRFAC 串并联复合同步控制设计与仿真

由上一节分析可知，需要在系统中构造合适的自适应规律，使得缸1 和缸2的偏差信号e根据自适应规律产生反馈作用去修正调节器的参数，从而使可调节系统的输出Y与参考模型的输出在整个时间历程上尽量保持一致。

电液伺服系统的非线性特性和参数不确定性是制约其控制算法发展的两个主要因素，而且它们的非线性环节又是未知和时变的[10]。模糊控制在解决复杂的、不清楚的、不确定的系统时显得非常有效。这是因为模糊控制由语言性控制规则构成，对于输入和输出变量之间的关系，采用条件语句描述，因而不需要系统精确的数学模型，可应用于数学模型不确定甚至模型未知的系统[12]。此外，将模糊控制与自适应控制相结合，也有其独特的优势。因为自适应控制需要辨识出对象精确的数学模型，并且自适应机构一般较复杂，因而在工程应用中，其实时性受到一定的限制[13]。而用模糊控制器进行参数整定不需要进行参数自适应律的推导，这是其他方法所不可比拟的。

综上所述，作者经过仿真实验，以及参阅相关文献，最终确定了模型参考模糊自适应(MRFAC)的控制方案。

5.1 MRFAC的原理

MRFAC是利用模糊逻辑实现系统的自适应控制，控制原理图如图13所示，即将图10中的常规自适应控制律用模糊控制律来代替。模糊自适应机构的输入设为系统广义误差e 及其变化率de/dt，Ke和Ke'为模糊系统输入量化因子;由于原系统中已采用PID控制器作为前馈控制，这里将自适应机构的输出作为PID控制器的3个系数Kp、Ki、Kd的增量，构成模糊PID自适应机构，从而对PID控制器的3个系数进行在线调节，使系统动态响应加快，超调量变小，而且整个响应过程具有较好的鲁棒性[14]。

图13 模型参考模糊自适应控制原理图

当液压伺服系统的动态参数发生变化时，自适应机构根据广义误差e 及其变化率de/dt的大小，通过模糊自适应机构给出一个调节信号反馈到可调系统中，以保证液压伺服系统的输出准确地跟随缸1的输出。研究表明:调整输入模糊控制器的量化因子和比例因子，实际上是把模糊控制器中的论域划分压缩或者扩张，与变论域模糊控制系统本质上相同。在此通过模糊因子自调整律实时调整模糊自适应机构的输入输出因子，实现变论域模糊控制，实际上等于增加了模糊规则，从而提高了模糊自适应机构输出调整精度[15]。

5.2 MRFAC控制器设计

在该系统中，模糊控制器的具体设计步骤如下:

(1)选择模糊控制器的输入输出变量，定义各变量的模糊子集。模糊控制器的输入变量为误差e 及其变化率de/dt。而其输出变量为PID控制器3个参数的调整量ΔKp、ΔKi、ΔKd的。它们分别被规定为下列Fuzzy 子集:

{NB，NM，NS，Z，PS，PM，PB}

(2)确定输入量和输出量各自的论域，建立各自的隶属度函数。误差e的论域为[－3，3]，de/dt的论域为[－3，3]，ΔKp的论域为[－2.5，2.5]，ΔKi的论 域为[－0.06，0.06]，ΔKd的论 域为[－0.3，0.3]。各模糊子集的隶属函数如图14所示，这里只列举误差e的隶属度函数，其他的与之相似，不再赘述。

图14 模糊子集的隶属函数

(3)建立模糊控制器的控制规则。根据系统的实际控制需要，建立在线调整比例因子ΔKp、ΔKi和ΔKd的模糊控制规则表[16]，见表2—4。

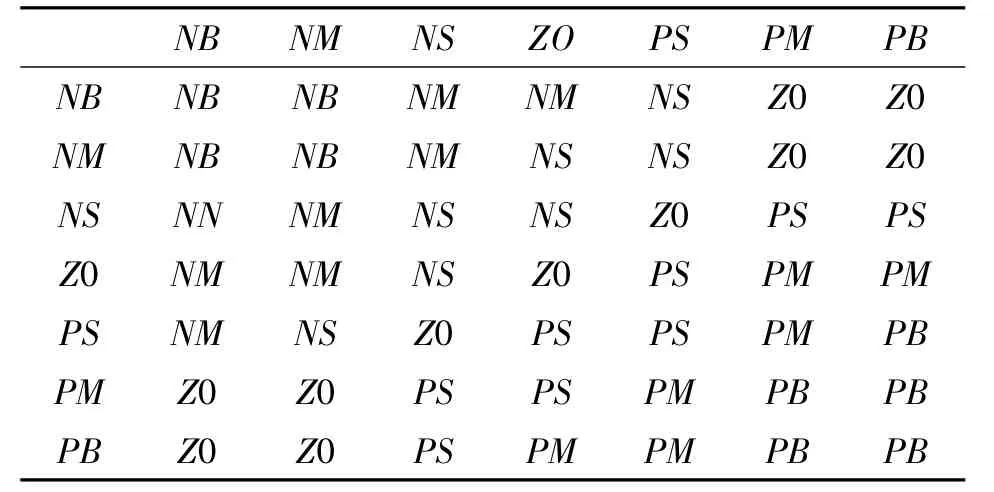
表2 ΔKp的模糊控制规则表

表3 ΔKi的模糊控制规则表

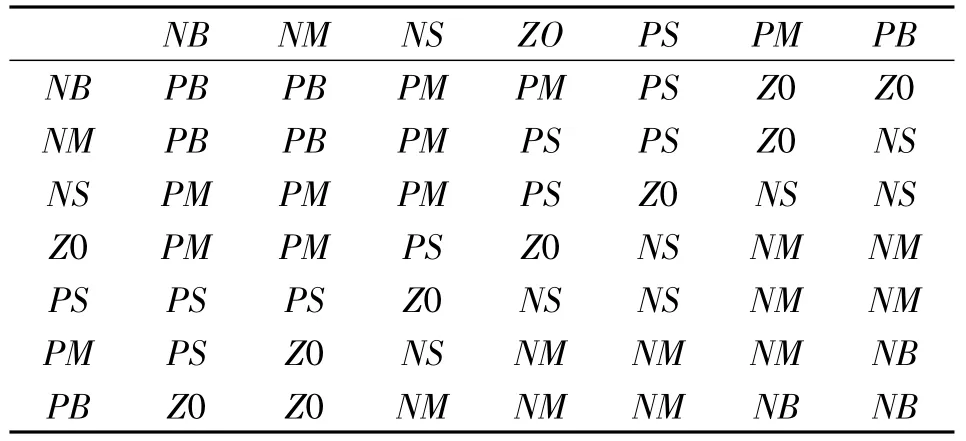
表4 ΔKd的模糊控制规则表

(4)反模糊化时，若采用重心法，结果精确但软件实现较困难;采用最大值法，虽结构简单，但结果不精确。所以选用加权平均法，兼顾了二者的优点[17]。加权平均法可用下式表示:

式中:μ(Ui)为各元素Ui在集合中的隶属度;

Ci为各元素在集合中的加权系数。

(5)量化因子Ke、Ke'的选择。MRFAC系统结构中，模糊自适应机构的输入为系统输出偏差。模糊自适应机构的作用是使系统输出动态偏差尽快减小。系统输出偏差的大小反映了系统的自适应性能。因此，作者结合对系统精度的要求来选择量化因子。选择量化因子为:

一般，系统要求的精度为1%～3%，此系统误差精度为2%。所以一般选择Ke=30～100，Ke'=100～500。

5.3 实验与结果讨论

5.3.1 仿真结果与分析

根据上述控制原理和设计参数，绘制Simulink仿真实验框图如图15所示。这里只显示从动缸的仿真框图，运行仿真，MRFAC的单位阶跃响应如图16所示;MRFAC控制算法下的同步误差与传统PID算法下的同步误差比较如图17所示。

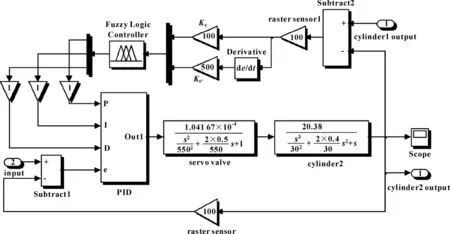
图15 MRFAC 同步控制仿真框图

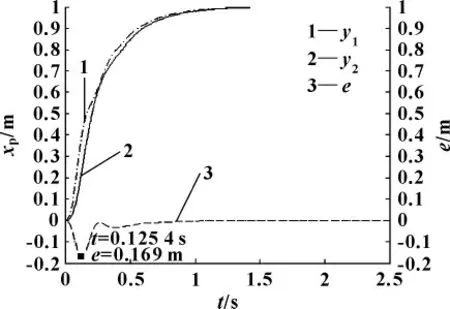
图16 MRFAC 同步控制仿真结果

从图16中可以清楚地看出:与未加模糊自适应相比，在参数变化量相同时，传统PID 超调较大，而MRFAC的同步误差得到了很好的改善。虽然改善的量不大，但是对于系统本身物理因素所导致的动态同步误差的调节，哪怕使之减少一点都是很难得的。此时，最大动态同步误差仅为0.169 m，稳态同步误差达到了2.0×10－2mm。

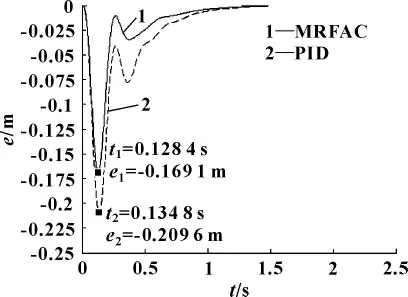
图17 同步误差比较

从图17可以看出:加有MRFAC控制的从动缸显然收敛得更快，这使得从动缸达到稳态的时间缩短为1.3 s 左右，从而使两缸更快地达到了同步，而且缸2 在整个时间历程上能很好地跟踪缸1的位移，从而实现模具研配时的精确同步控制。

5.3.2 鲁棒性验证

用两种干扰来检验MFAC的鲁棒性。首先，将开环增益增大一倍来模拟外界一个简单的干扰，其仿真曲线如图18所示。此时PID控制的从动缸的输出曲线明显出现振荡变坏的现象，而MRAFC 无超调，其响应曲线与初始状态响应区别较小。

图18 开环增益增大一倍后的从动缸跟踪曲线

进而利用MATLAB 自带的限带白噪声干扰信号，将其叠加到从动缸的输入中，模拟外界的一个复杂噪声，对比两种控制算法的输出响应，如图19所示，两者的同步误差信号输出如图20所示。由图19、20可知:虽然两个输出均出现了不同程度的震荡，但是可以看出MRFAC 所产生的震荡明显小于传统PID算法。可见文中提出的MRAFC 具有很好的鲁棒特性。

图19 加入白噪声后的从动缸跟踪曲线

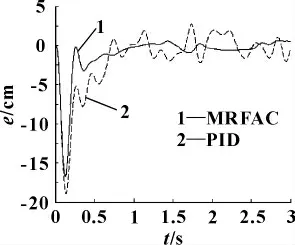
图20 加入白噪声后的同步误差曲线

6 结论

通过比较常用的液压典型同步回路，结合模具研配压力机的设计要求，确定了在主油路上采用双比例流量阀，并且在旁路采用伺服阀同时控制的双缸同步下行控制方案。建立了阀控非对称液压缸及主动缸液压伺服系统的数学分析模型。通过对主动缸液压伺服系统进行时域和频域分析，对系统进行了PID校正，改善了系统的响应速度。

在进行同步设计时，利用MATLAB/Simulink 对串联和并联同步控制进行了仿真，结合二者各自的优点，设计了使用于该压力机的串并联复合同步控制系统，实验发现双缸运行基本同步，最大动态误差仅为0.169 m，因此获得了较为满意的控制双缸同步下行效果。进而，利用基于模型参考的模糊自适应控制算法对系统进行了改进。实验证明:加有MRFAC控制的从动缸的响应收敛得更快，而且在整个时间历程上能很好地跟踪缸1的位移，从而实现模具研配的精确同步控制。最后，利用增大开环增益和限带白噪声来模拟叠加于输入的外界干扰，仿真实验证明MRFAC控制算法的鲁棒性较之PID算法有明显的优势。

【1】奇瑞公司.奇瑞汽车股份有限公司三厂研配压机技术协议[R].2009:1－10.

【2】隨云龙.模具研配液压机双缸同步液压系统的动态特性研究[D].沈阳:沈阳工业大学，2005:9－10.

【3】俞新陆.液压机的设计与应用[M].北京:机械工业出版社，2007.

【4】张宏.PLC控制模具研配液压机系统的研究[D].沈阳:沈阳工业大学，2003:9.

【5】韩国惠.PLC控制模具研配液压机双缸同步控制的研究[D].沈阳:沈阳工业大学，2005.

【6】宋志安.基于Matlab的液压伺服控制系统分析与设计[M].北京:国防工业出版社，2007:195－205.

【7】夏德钤.自动控制原理[M].北京:机械工业出版社，1989.

【8】苏东海，杨京兰.基于SIMULINK的阀控非对称液压缸系统的研究[J].流体传动与控制，2008(1):3－5.

【9】王野牧，王洁.液压伺服闭环控制系统的SIMULINK仿真实现[J].沈阳工业大学学报，2005，22(5):370－372.

【10】管杨新，胡大邦，王奕豫.电液位置同步伺服系统的模糊控制研究[J].机床与液压，2002(1):83－85.

【11】王占林.近代电气伺服液压控制[M].北京:北京航空航天大学出版社，2005:56－88.

【12】CHEN Cheng-Yi，LIU Li-Qiang，CHENG Chi-Cheng，et al.Fuzzy Controller Design for Synchronous Motion in a Dual-cylinder Electro-hydraulic System[J].Control Engineering Practice，2008(16):658－673.

【13】刘国荣.模型参考自适应控制[J].控制原理及应用，1996(1):92－97.

【14】方一鸣，黄镇海，焦晓红.液压伺服位置系统模型参考模糊自适应PID控制器的设计[J].自动化与仪器仪表，2002(3):6－11.

【15】李洪兴.变论域自适应模糊控制器[J].中国科学E辑，1999，29(1):32－421.

【16】刘金琨.先进PID控制及其Matlab仿真[M].北京:电子工业出版社，2003:67－80.

【17】KIM Jong-Hwan，LEE Seon-Woo，KIM Kwang-Choon.Fuzzy Precompensation of PID Controller[C]//Proceeding of Second IEEE Conference on Control Application，1993.