特殊爪型真空泵转子型线的研究

2013-03-20徐学忠谭翰墨刘建花

机床与液压 2013年5期

徐学忠，谭翰墨，刘建花

(常熟理工学院机械工程学院，江苏常熟215500)

引言爪型干式真空泵是一种非接触式的干式真空泵，它具有无油、较大的压缩比、可直接向大气排气、可处理固体颗粒等优点，特别适合于电子产品等工艺的真空设备中。

爪型真空泵转子型线主要有6段曲爪式、7段直爪式和非对称爪型等几种。但其转子型线都是由直线、圆弧、摆线及其包络线连接而成。6段曲爪式和7段直爪式真空泵由于啮合两转子型线完全相同，称为对称型转子型线;另一类爪式真空泵其啮合两转子的型线完全不相同，称为非对称型或特殊型。由于转子型线组成多样性，共轭曲线的计算求解较复杂，给设计工作带来诸多不便，影响了其推广应用和使用性能的提高。

文献[1－2]对真空泵的型线进行了研究，但都是采用直角坐标变换和公式进行求解。这种方法所得到的方程较复杂，求解较麻烦。作者应用复数矢量法对一种特殊爪型真空泵的理论型线进行了研究，建立了两转子曲线方程，运用计算机作出了转子型线，并对泵的容积利用系数进行了研究，提出了影响容积利用系数的主要因素。

1 坐标系的建立

以转子1的回转中心O1为原点建立静坐标系X1O1Y1;以转子2的回转中心O2为原点建立静坐标系X2O2Y2;动坐标系x1O1y1以O1为原点，固结于转子1 上;动坐标系x2O2y2以O2为原点，固结于转子2 上。

转子型线上处于啮合的点M可表示在上述4个坐标系中，这些坐标系具有下列变换关系:

设啮合点M 在静坐标系中的矢径为r(fk)M，上标k表示点M 所在的动坐标系，k=1，2;而点M 在动坐标系中的矢径为r(sk)M。

图1 坐标系的建立

两静坐标系之间的变换关系为

两动坐标系之间的变换关系为

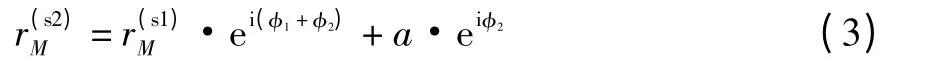
式中:a为两转子的中心距;

φ1、φ2为动坐标系相对于静坐标系的转角。

真空泵两转子之间的传动是传动比为1的定传动比传动，故有

式中:R1、R2为两转子的节圆半径。

2 转子型线的曲线方程

2.1 转子1组成

所研究的特殊爪型真空泵转子的一对转子形状是不同的，相互啮合的转子1 和转子2的型线是中心对称的，其由圆弧、直线或摆线以及它们的共轭曲线组成。

设爪顶圆半径为Rm=c·R，R1=c1·R、R2=c2·R，中心距a=2R，其中:c为形状系数;c1为爪顶系数;c2为爪背系数;R为节圆半径。

转子1 (图2)各段的组成为:AB段为摆线，与转子2 上右侧的尖点共轭;BC段为圆弧，半径为R1，圆心在点O1(Rm－R1，0);CD段为直线，平行于x轴且距x轴的距离为R1，与BC 圆弧相切，点D坐标为(Rm－a－R2，R1);DE段为圆弧，半径为R2，圆心在点O2(Rm－a－R2，R1－R2);EF段为直线，其与y轴平行，与圆弧DE 相切。FG段也为摆线，与转子2 上的点F 共轭，与AB段中心对称。

转子下半部分型线关于中心对称，只要求出上半部分的型线就可以了。各段曲线参与啮合时，啮合点M 在动坐标系上的轨迹即为相应段的轮廓曲线。现在已知转子1的轮廓曲线，求与其共轭的转子2的曲线。

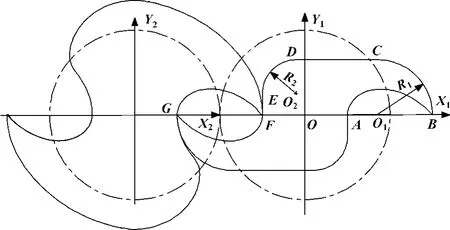
图2 转子型线

2.2 各段曲线方程

BC段啮合时，如图3所示，啮合点M 在静坐标系x1O1y1中矢量方程

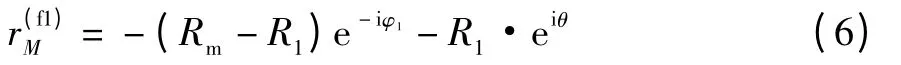
上式中角参量θ、φ1和α之间的关系

图3 BC段啮合图

CD段为直线，平行于x1轴且距x1轴的距离为R1，点D坐标为(Rm－a－R2，R1)。

CD段啮合时 (图4)，啮合点M 在动坐标系x1O1y1中矢量方程

点M 由点D 到点C时，φ1的变化范围为φ1D～φ1C，由几何关系可得

动坐标系中x1轴相对于静坐标系中X1轴的转角为

图4 CD段啮合图

DE段啮合时 (图5)，啮合点M 在静坐标系X1O1Y1中矢量方程

其中:a2为OO2间的距离

角参量θ、φ1之间的关系为

OO2与y1轴所夹角度为

点E 啮合时，对应的角度θ为

点D 啮合时，对应的角度φ1D

在转子转动过程中，φ1的变化范围为φ1=－φ1D～φ1E。动坐标系中x1轴相对于静坐标系X1轴的转角为

图5 DE段啮合图

EF段啮合 (图6)时，啮合点M 在动坐标系x1O1y1中的矢量方程

其中:φ1的变化范围为0～φ1max

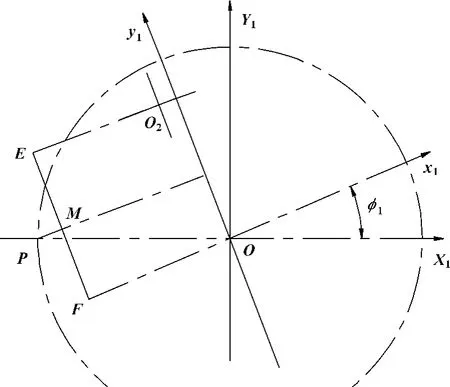
图6 EF段啮合图

FG段为一段摆线，由转子2 上的相应一点F 共轭形成，在静坐标f2中，点F 作圆周运动，半径为Rm，在动坐标系s2 中其矢量方程为

动坐标系中x1轴相对于静坐标系中X1轴的转角为φ2=0～arccos(1/c)。

转子1 上的点G与转子2 上的一段摆线共轭，点G 在静坐标f1 中作圆周运动，半径为Rm，在动坐标系s1 中其矢量方程为

点G与转子2 上的点啮合时，动坐标系中x1轴与静坐标系中X1轴的夹角φ1的变化范围为φ1=－arccos (1/c)～0。

以上是转子型线上半段的求解过程，当求出啮合点M 在任一坐标系中的轨迹方程和动坐标系相对于静坐标系的转角，通过坐标变换就可以求出另一转子的型线方程。另外，由于两转子都是中心对称的，根据上半部分的曲线矢量方程容易求出下半部分的曲线方程。

图7为根据以上求得的曲线方程，用MATALB软件作出的两转子型线。参数取值:R=50 mm，c=1.5，c1=0.65，c2=0.4。

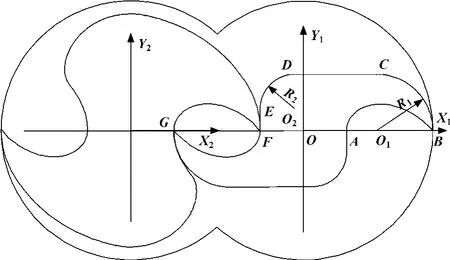
图7 转子型线图

这里所研究的转子型线与文献[1]所研究的型线的不同之处是:该转子1的EF段是一铅垂直线，而文献[1]中此段曲线是由3段互相相切的圆弧组成，其设计参数要增加2个。理论计算和作图可证明:用直线代替3段圆弧对曲线的形态和特性不产生影响，但可使曲线的求解变得简单。

3 容积利用系数

变容式真空泵中，其几何抽速的大小与容积利用系数λ 有关，在其他条件一定的情况下，λ 愈大，表示几何抽速也就愈大。

容积利用率是指转子旋转一周的有效吸气容积与转子一周所扫过的容积之比。如图8所示，转子旋转半周，形成两个吸气容腔A2s和A1s，半周内有效吸气面积为

在此过程中，转子扫过的面积为Ars=π·R2m，则容积利用系数为

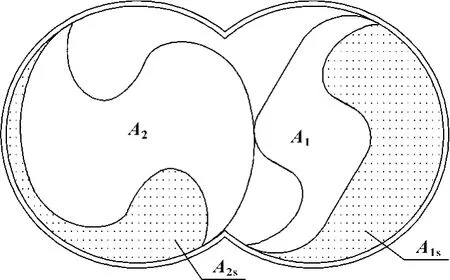
图8 转子的吸气排气容积图

求得转子曲线方程后，两个转子的横截面积可通过积分求出，从而可求出泵的容积利用系数。

通过分析计算可知，影响转子型线和泵的容积利用系数的参数有形状系数c、爪顶形状系数c1和爪背形状系数c2。表1列出了几组参数下的容积利用率值。

表1 容积利用系数变化表

由表中计算可知:随着形状系数c的增大，容积利用率也随着增大。但随着c的增大，转子的爪尖部分变尖，强度变弱，爪根与轴联接处变细，联接强度降低，因此提高容积利用系数受到限制。爪顶系数c1和爪背系数c2的取值对容积利用系数的影响较小，它们的取值主要考虑其对转子形状的影响，如保持转子各段曲线平滑连接、共轭曲线不出现内凹等条件。表1中的容积利用系数也较文献[1]相近系数型线所得容积利用系数有所增大。