基于视觉的智能车辆模糊滑模横向控制

李琳辉，李 明，郭景华，连 静＊

（1.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024；2.大连理工大学 运载工程与力学学部 汽车工程学院，辽宁 大连 116024）

0 引 言

随着汽车保有量的不断增加，交通事故也持续增加，惨剧的不断发生使汽车安全问题成为公众日益关注的焦点.近年来，随着科技的不断发展进步，汽车安全辅助驾驶技术作为智能车辆发展的重要组成部分，已成为国内外专家学者研究的热点，因为它能够在一定程度上降低由于疲劳和疏忽等原因引发的事故概率.目前比较成熟的汽车安全辅助驾驶技术，如车道保持系统和自动泊车系统，都离不开车辆的横向控制.横向控制主要是指控制车辆在不同的车速、路况、荷载以及风阻等条件下自动跟踪期望轨迹，并能够保持一定的舒适性和平稳性［1］，主要考查的是车辆的路径跟踪能力，即如何控制车辆沿给定参考路径行驶.

车辆的横向控制一直是车辆控制中的难点，目前已经有很多专家学者对它进行了研究.文献［2］采用经典PID 控制方法设计车辆横向控制器，它具有良好的跟踪能力，但是缺乏对复杂工况的适应性.文献［3］采用最优控制理论设计有限时间最优预瞄横向控制器，但它对外部干扰的鲁棒性较差，降低了跟踪过程中车辆的稳定性.文献［4］基于滑模控制理论设计车辆横向控制器，它对系统参数摄动和外界干扰具有完全的鲁棒性且响应速度快，但是在滑动面附近由于高频转换控制会产生高频抖振现象，这种抖振会造成车辆转向的不稳定和车辆的机械磨损，对人员安全有害.文献［5］采用模糊控制方法来设计横向控制器，不需要精确的数学模型，对参数变化和外部干扰的鲁棒性比较强，在系统模型不确定的情况下，能够根据操作人员的经验和专家的知识给出可行的方法设计控制器，但是难以根据系统特性进行自适应的调整，容易产生稳态误差.

基于上述原因，本文提出一种模糊控制和滑模变结构相结合的智能车辆横向控制方法，将两种控制思想的优点结合起来，采用滑模切换函数及其变化率作为模糊控制的输入，一方面保持滑模变结构对系统参数摄动和外部干扰具有鲁棒性的特性；另一方面保持常规模糊控制器不依赖系统模型的优点，同时柔化控制信号，减轻甚至避免一般滑模控制容易出现的抖振现象.

1 车辆视觉预瞄运动学模型

人们在驾驶的过程中往往会习惯性地提前观察前方的道路，对前方的道路情况预先进行估计，根据经验在适当的时候提前转动方向盘，来保证车辆按照驾驶者的意图行驶.对于基于视觉的智能车辆来说，需要根据预瞄点处的横向偏差和方位偏差等信息，按照一定的策略来控制车辆按照参考路径行驶.

本文研究的智能车辆视觉导航系统由CCD摄像机、图像采集卡、监视器和导航计算机四部分组成.通过前置CCD 摄像机实时获得前方道路的环境信息，通过串口将获取的信息传递给计算机，然后对获取的信息进行数字图像处理，获取车辆预瞄点处的横向偏差和方位偏差.车辆视觉预瞄运动学示意图如图1所示.

图1 车辆视觉预瞄运动学示意图Fig.1 Sketch map of vehicle preview kinematics

从图1所示推导可知，基于视觉的预瞄运动学模型 可以表达为［6－8］

式中：yl为车辆视觉预瞄点处车辆中心线与路径的横向偏差（m）；εl为车辆视觉预瞄点处车辆中心线与路径切线的夹角（rad）；vx为车辆纵向速度；vy为车辆横向速度；L代表预瞄距离（m）；κl为路径曲率；ψ为车辆横摆角.

2 综合偏差的确定

为了使模糊控制系统结构的复杂性降低，算法更易于实现，本文将控制目标从综合偏差转为滑模切换函数，只要施加控制使滑模切换函数为零，综合偏差也会渐近到达零点，因此选择综合偏差作为滑模切换函数的参数.综合偏差即横向偏差和方位偏差融合后的偏差，由于横向偏差和方位偏差都具有量纲，需要将它们量纲一化，将量纲一化后的横向偏差和方位偏差εl融合为el，并定义el为综合偏差，其表达式为

式中：η1、η2 为系数，且η1 ＋η2 ＝1.

3 控制器设计

为了克服常规滑模横向控制的不足，本文设计了一种模糊滑模控制的方法，它既能够缩短滑模到达时间，又能够达到削弱抖振的目的.通过将智能车辆视觉系统采集到的横向偏差yl和方位偏差εl融合为综合偏差el，并作为滑模切换函数s的参数，将滑模切换函数及其变化率作为模糊控制的输入，前轮转向角δf作为输出来控制智能车辆的横向运动，其控制器结构如图2所示.

图2 模糊滑模控制器结构图Fig.2 Block diagram for fuzzy sliding mode controller

3.1 滑模面

根据式（2）所得到的综合偏差el及其变化率，设定滑模变结构控制的切换函数为s，其表达式为

如果达到理想的滑模控制，则＝0，联合式（3）可以得到

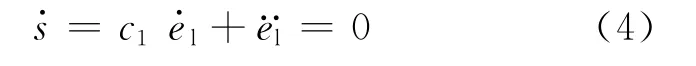
式中：c1为常数为综合偏差变化率为综合偏差变化率的导数.

3.2 模糊滑模控制

为了达到通过模糊控制思想优化滑模控制器的目的，本文选择s和s·作为模糊控制器的输入变量，选择前轮转角δf作为模糊控制器的输出变量.为了克服外界干扰及参数不确定性的影响，满足运动存在的条件，并且削弱滑模控制所引起的抖振，根据经验，利用模糊控制规则来调整控制变量δf大小，确保存在和到达条件s＜0成立.

本文采用双输入单输出模糊控制器，由输入变量s、和输出变量δf构成，将它们分别转化到论域为X［－1，1］、Y［－1，1］和Z［－1，1］的模糊集F、Fc和T，输入变量s、和输出变量δf对应模糊子集语言变量均为｛NB，NM，NS，ZO，PS，PM，PB｝，其中NB、NM、NS、ZO、PS、PM、PB 分别称为负大、负中、负小、零、正小、正中、正大.输入变量s、和输出变量δf的模糊子集隶属度函数由Z形函数、三角函数和S形函数组成，如图3～5所示.

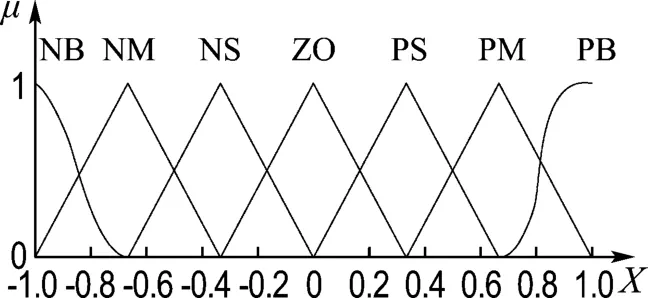
图3 滑模面s的隶属度函数Fig.3 Membership functions of sliding mode surfaces

图4 滑模面s ·的隶属度函数Fig.4 Membership functions of sliding mode surface s ·

图5 前轮转角δf 的隶属度函数Fig.5 Membership functions of front wheel steering angleδf

3.3 模糊控制规则

模糊控制规则是模糊控制器的核心，决定着模糊控制器的性能，它通过模糊逻辑的模糊条件语句来表征人类驾驶行为的经验知识，提供了一种简单描述人类驾驶行为的方法.本文的模糊控制规则由49 条“IF－THEN”规则组成，即R＝｛R1，…，R49｝，其中每一条规则都由下面形式的“IF－THEN”模糊语句构成：

Ri：IFsisFiANDisFci，THENδfisTi其中Fi、Fci和Ti分别为输入变量s、和输出变量δf模糊子集的语言变量：

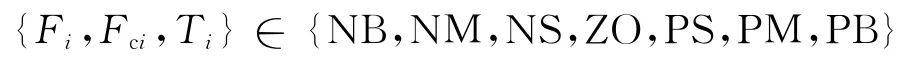
根据人类驾驶车辆积累的经验及控制规则的要求，本文所设计的模糊控制规则如表1所示.

表1 模糊控制规则Tab.1 Rule－base of FSMC

3.4 模糊推理及反模糊化

作为模糊控制的核心，模糊推理根据模糊控制规则给出合适的控制量，本文采用比较常用的Mamdani推理法.

模糊推理后产生的控制量，需要通过反模糊化转换为智能车辆执行机构可以接受的精确量.本文采用重心法进行反模糊化［8］.

式中：δfb表示模糊控制器输出的反模糊以后的精确值，δfi表示模糊控制论域中的值，μsi表示δfi的隶属度的值.

4 仿真分析

为了测试本文所设计的横向控制策略对参考路径的跟踪效果，在Matlab／Simulink 环境下进行了仿真研究.本文采用十二自由度整车动力学仿真模型［9］，主要模型参数参考课题组开发的DLUIV－1型智能车辆试验样车，车辆参数如表2所示.

表2 DLUIV－1车辆参数Tab.2 DLUIV－1vehicle parameters

4.1 工况Ⅰ仿真分析

仿真所用的参考路径Ⅰ如图6所示，0～10s为直线，检验控制器跟踪直线的效果；10～20s为曲率为0.005m－1的弯曲路径，检验控制器跟踪弯路的效果；20～30s为直线，检验从弯路变为直路时控制器的跟踪效果；30～40s 为曲率为－0.01m－1的弯曲路径，检验从直路变为弯路时控制器的跟踪效果；40～50s是曲率为0.008 m－1的弯曲路径，检验从曲率－0.01m－1急剧变为0.008m－1这种恶劣工况下控制器对路径的跟踪效果；最后是一段直线.

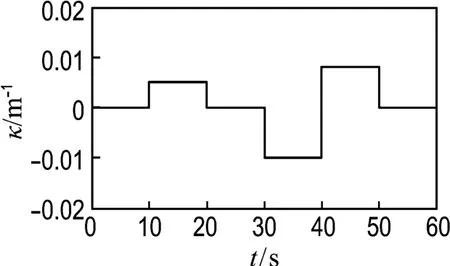
图6 参考路径ⅠFig.6 Reference path Ⅰ

设置车辆的初始横向偏差为0.2 m，初始方位偏差为0.1rad，滑模参数c1＝10，纵向车速vx＝5m／s，预瞄距离L＝5m.图7给出了分别采用滑模控制器和模糊滑模控制器跟踪参考路径Ⅰ的过程中，控制器输出的车辆前轮转角变化的对比曲线.可以看出采用滑模控制器时，在路径曲率发生变化的位置会有抖振产生，这会影响车辆的稳定性；而采用模糊滑模控制方法的控制器能很好地削弱这种抖振，提高轨迹跟踪的稳定性.图8给出了采用模糊滑模控制算法车辆的横向和方位偏差响应曲线，可以看出横向偏差控制在±0.015 m，方位偏差控制在±0.029rad，表明该控制算法可以准确稳定地跟踪不同曲率组成的参考路径.

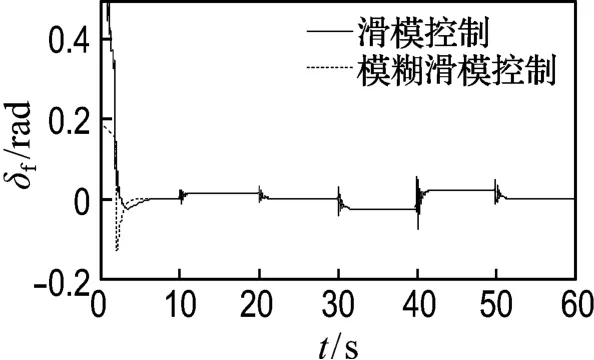
图7 前轮转角响应曲线Fig.7 The response curve of front wheel steering angle

图8 vx＝5m／s时横向和方位偏差仿真结果Fig.8 Simulation results of lateral and direction errors when vx ＝5m／s

由于车辆在行驶过程中，其各种物理参数是不断变化的，需要通过仿真来检验参数改变对车辆路径跟踪性能的影响，测试所开发的控制算法对车辆参数变化的适应性.

首先，令车辆荷载在±400kg范围内按正弦曲线变化，此时的横向和方位偏差响应如图9所示，横向偏差控制在±0.023m，方位偏差控制在±0.03rad，可以看出所提出的控制算法对车辆荷载的变化有比较强的适应性.

然后，将纵向车速提高至vx＝10 m／s，此时的横向和方位偏差响应如图10所示，可以看出横向偏差控制在±0.01m，方位偏差控制在±0.02 rad，亦可以看出在车速变化的情况下所提出的控制算法仍然能够很好地跟踪参考路径，而且具有较快的收敛速度，曲线变化比较柔和，能够有效抑制抖振现象.

图9 荷载按正弦变化时横向和方位偏差仿真结果Fig.9 Simulation results of lateral and direction errors when vehicle′s mass change according to sinusoidal variation

图10 vx＝10m／s时横向和方位偏差仿真结果Fig.10 Simulation results of lateral and direction errors when vx ＝10m／s

为了检验算法对于车辆在高速情况下的跟踪能力，将纵向车速提高至vx＝20 m／s，此时的横向和方位偏差响应如图11所示，虽然开始时振动稍大，但是很快会趋于平稳，且横向偏差控制在±0.08m，方位偏差控制在±0.08rad，可以看出速度的增加在一定程度上对横向和方位偏差有影响，但是该控制算法都能保证跟踪的稳定性，不会出现抖振，曲线变化相对平滑柔和稳定.

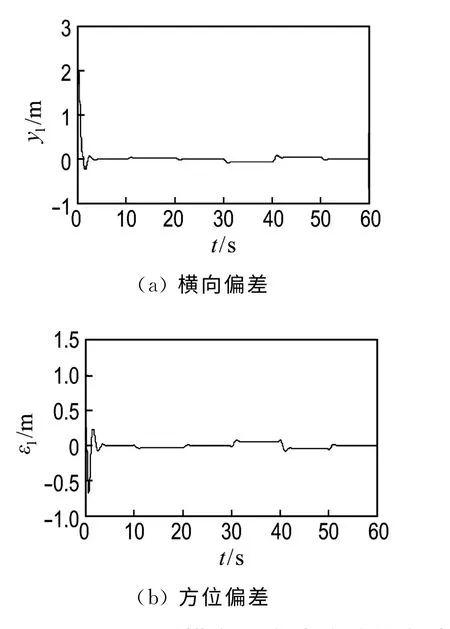
图11 vx＝20m／s时横向和方位偏差仿真结果Fig.11 Simulation results of lateral and direction errors when vx ＝20m／s

此外，还通过改变轮胎的侧偏刚度和预瞄距离以测试这两个参数的变化对车辆横向控制的影响，横向和方位偏差均稳定在一定数值范围内，没有出现抖振现象，这表明本文所提出的模糊滑模控制算法对车辆主要参数的变化均具有较强的鲁棒性，能够满足稳定且准确地跟踪参考路径的要求.

4.2 工况Ⅱ仿真分析

为了更好地检验所设计的模糊滑模横向控制算法在复杂路况下对车辆横向控制的效果，设计参考路径Ⅱ如图12所示，相比参考路径Ⅰ，路径曲率变化得更快，车辆跟踪路径所处的工况环境更为恶劣.仿真结果如图13和14所示，分别表示前轮转角、横向偏差和方位偏差响应曲线.通过对仿真曲线的分析可以看出，虽然工况更为恶劣，但是前轮转角响应曲线变化平稳，没有出现抖振，保证了方向盘转动的稳定性，同时横向偏差和方位偏差都稳定在很小的范围内，分别为±0.03m 和±0.07rad，说明所提出的控制算法能够准确、稳定地跟踪复杂的参考路径，对车辆参数的变化具有较强的鲁棒性，满足智能车辆横向控制的要求.

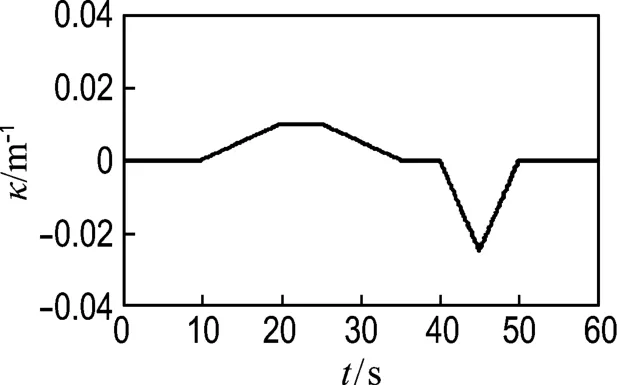
图12 参考路径ⅡFig.12 Reference path Ⅱ

图13 前轮转角Fig.13 Steering angle of front wheel

图14 横向和方位偏差模拟结果Fig.14 Simulation results of lateral and direction errors

5 结 语

本文针对基于视觉预瞄的车辆横向模型，研究并提出了模糊滑模横向控制算法，即由横向偏差和方位偏差融合的综合偏差来构成滑模面，采用滑模切换函数及其导数作为模糊控制的输入变量，不同于以往采用综合偏差作为模糊控制输入变量，这种改变能更好地克服参数不确定性及外界干扰的影响，并且削弱滑模控制所引起的抖振现象，确保了跟踪控制过程中车辆的方向盘转动的稳定性.仿真结果表明该控制算法能够保证智能车辆稳定准确地跟踪参考路径，满足智能车辆自主导航对车辆横向控制的要求.

［1］ Netto M，Blosseville J，Lenoit B.A new robust control system with optimized use of the lane detection data for vehicle full lateral control under strong curvature ［C］ ／／ IEEE Intelligent Transportation Systems Conference.Piscataway：IEEE，2006：1382－1387.

［2］ 赵熙俊，陈慧岩.智能车辆路径跟踪横向控制方法的研究［J］.汽车工程，2011，33（5）：382－387.ZHAO Xi－jun，CHEN Hui－yan.A study on lateral control method for the path tracking of intelligent vehicles［J］.Automotive Engineering，2011，33（5）：382－387.（in Chinese）

［3］ 马 莹，李克强，高 峰，等.改进的有限时间最优预瞄横向控制器设计［J］.汽车工程，2006，28（5）：433－438.MA Ying，LI Ke－qiang，GAO Feng，etal.Design of an improved optimal preview lateral controller［J］.Automotive Engineering，2006，28（5）：433－438.（in Chinese）

［4］ Tai M，Tomizuka M.Experimental study of lateral control of heavy vehicles for automated highway systems［C］／／Proceedings of the American Control Conference.Anchorage：ACC，2002：851－865.

［5］ Trabia M B，Shi L Z，Hodge N E.A fuzzy logic controller for autonomous wheeled vehicles［M／OL］／／ Mobile Robots，Moving Intelligence，2006：175－200.http：／／www.intechopen.com／books／mobile＿robotics＿moving＿intelligence／a＿fuzzy＿logic＿controller＿for＿autonomous＿wheeled＿vehicles.

［6］ 马 雷，王荣本.智能车辆导航控制技术［J］.吉林大学学报：工学版，2004，34（4）：582－586.MA Lei，WANG Rong－ben.Intelligent vehicle steering control［J］.Journal of Jilin University：Engineering and Technology Edition，2004，34（4）：582－586.（in Chinese）

［7］ Kosecka J，Blasi R，Taylor C J，etal.A comparative study of vision－based lateral control strategies for autonomous highway driving［C］／／Proceedings of the IEEE International Conference on Robotics and Automation.Piscataway：IEEE，1998：1903－1908.

［8］ 曾光奇，胡均安，王 东，等.模糊控制理论与工程应用［M］.武汉：华中科技大学出版社，2006.ZENG Guang－qi，HU Jun－an，WANG Dong，etal.Fuzzy Control Theory and Engineering Application［M］.Wuhan：Huazhong University of Science ＆Technology Press，2006.（in Chinese）

［9］ 郭孔辉.汽车操纵动力学［M］.吉林：吉林科学技术出版社，1991.GUO Kong－hui.Dynamics of Controllability Automobile［M］.Jilin：Jilin Science and Technology Publishing House，1991.（in Chinese）