基于可变模糊数据包络分析的多目标决策模型

双 晴，袁永博，张明媛

（大连理工大学 建设工程学部，辽宁 大连 116024）

0 引 言

多目标决策问题是决策者在决策中经常遇到的实际问题，它是指在多个目标准则情况下确定一个方案好坏的决策过程，如生产规划、企业经济效益的综合评价、武器系统的优化设计等［1］.

多目标决策问题的关键步骤是目标权重的确定.各指标在决策中的地位不同，其差异主要表现在：（1）决策者对指标的重视程度不同；（2）指标在决策中的作用不同，即指标传达给决策者的信息量不同；（3）各指标价值的可靠程度不同.目前，指标权重确定的方法主要可以划分为主观赋权法和客观赋权法两种［2］.主观赋权法通过专家意见、问卷调查、通用准则等方式确定权重，如简单加权法、TOPSIS法［3］、加权平均规划法［4］等.客观赋权法试图通过实际数据寻找数据间的关系而生成客观权重，如变异系数法、熵法［5］等.然而，由于客观事物的复杂性及人类思维的模糊性，一般情况下，人们难以给出明确的偏好信息［6］，因此，能够直接反映数据关系的客观赋权法被认为更为有效和准确.

多目标决策问题的另一个关键要素是距离基准点的选择.通常样本与理想点距离越小越好.同时一些研究认为由于负理想点或非理想点为所构建样本中最劣集合，因此比较基准为距离最劣集合越远越好［7－8］.样本最终根据与理想点或非理想点的距离进行排序和择优.

本文通过优化每个决策指标的综合属性值得到客观权重，组合赋权并用可变模糊集理论与方法对决策单元进行排序，以避免指标偏好信息获取困难的问题，并修正数据包络分析方法中决策单元同时最优而难以择优的缺点，其相对隶属度的思想使决策单元的排序满足“距离理想点越近越好，距离非理想点越远越好”的思想，以便于计算机实现.

1 考虑权重客观度的可变模糊多目标决策模型

1.1 指标特征值规格化方式

设n个样本组成的集合为｛x1，x2，…，xn｝，共有m个指标特征值向量构成指标特征值矩阵：

其中xij为样本j指标i的特征值.为消除m个指标特征值物理量纲不同所带来的不可公度性，需要对指标特征值进行规格化，即要将指标特征值xij变换为对聚类样本关于模糊概念的指标相对隶属度rij.指标的规格化方式一般可分为效益型、成本型、固定型、偏离型、区间型等［9］，但以效益型和成本型最为通用.

效益型指标：特征值越大越优，规格化公式为

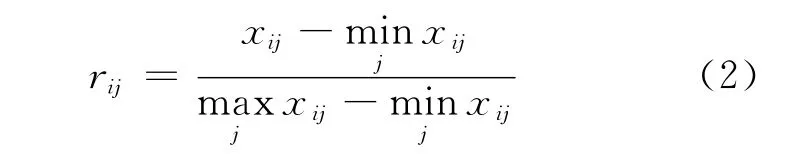
成本型指标：特征值越小越优，规格化公式为

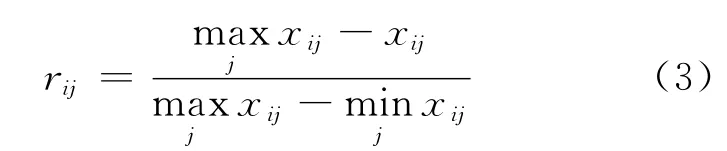
1.2 数据包络分析与客观权重

数据包络分析（DEA）是一种在具有多输入多输出的同水平决策单元（DMU）上评价相对效率的 方 法［10］.自 运 筹 学 家Charnes等［11］在1978年以相对效率概念为基础发展DEA 这一崭新的效率评价方法以来，模型的适用范围不断扩展，重要的理论结果不断出现，模型的实际应用也日益广泛.

多目标决策问题可以视为缺少投入量或每个决策单元具有相同投入量的DEA 问题［12］，可以证明，DEA 有效性与相应的多目标规划问题的Pareto有效解或非支配解是等价的［13］，因此，使用DEA 模型求解能够避免目标之间的冲突和无法比较的现象，为决策者提供一个较佳的解空间.其模型可表示为

其中Rij表示样本j指标i的特征值规格化数，wi为指标i的相对重要性权重，ε为非阿基米德无穷小，以方便使用单纯形算法求解模型.模型根据决策单元效率值所构建的超平面计算每个DMU的最优指标权重.模型的优势在于：（1）DEA 适用于复杂系统，能够从最有利于DMU 的角度进行评价；（2）投入产出向量间不必存在显示关系表达式，DEA 模型能够排除很多主观因素，具有更强的客观性.然而，尽管DEA 能够在优化权重的基础上求出每个DMU 的效率值，却很有可能出现多个DMU 同时达到效率值为1的情况，因此需要一种合理的机制帮助决策者进一步选择最优决策单元.

1.3 可变模糊多目标决策模型

1965年Zadeh创建的模糊集合是对普通集合的突破［14］，但模糊集合概念与定义的基石——隶属函数存在静态化的缺陷.在此基础上，可变模糊集理论根据自然辩证法中关于中介、差异、共维、两极的概念及客观事物矛盾运动变化的原理，建立了以对立模糊集概念为基础的模糊可变集合与可变模型集［15－16］.基本定义如下：

定义1 设论域U中的任意元素u的对立模糊概念或u对立的两种基本模糊属性，以与表示.在连续统区间［1，0］（对）与［0，1］（对）的任一点上，对立的两种模糊属性的相对隶属度分别为，且.令

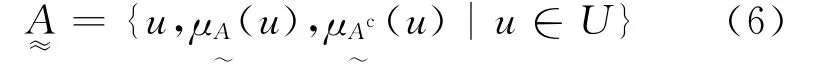
设s表示类别h的m个指标特征值规格化数，样本j与类别h之间差异的广义指标权距离公式为

为求解样本j隶属于类别h的最优相对隶属度u＊hj，引入以相对隶属度uhj为权重的加权广义指标权距离

建立目标函数［17－18］

满足约束条件

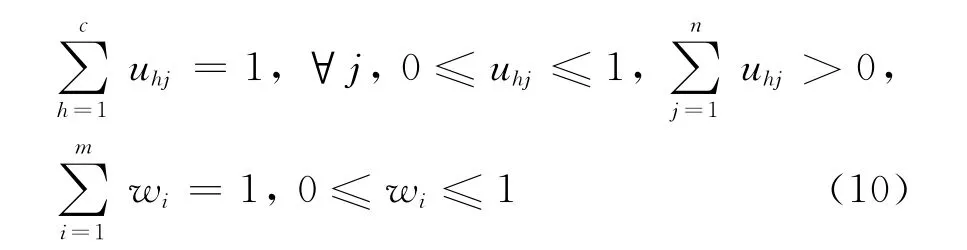
其中α为可变优化准则参数，α＝1、2分别为最小一、二乘方准则；p为可变距离参数，可取海明距离p＝1，欧式距离p＝2.

1.4 求解步骤

为将条件（10）极值（9）求解问题转化为无条件极值求解问题，构造拉格朗日函数（λu、λw分别为变量uhj、wi的拉格朗日乘子）：

并将c级识别简化为2级识别，则可得样本j对1级（优级）的相对隶属度

设计以下算法：

（1）对指标特征值矩阵X＝（xij）m×n按式（2）～（3）转变为指标特征值规格化矩阵R＝（rij）m×n；

（2）将指标特征值规格化矩阵R代入模型（5）求得对应于各指标的最优目标权重矩阵W＝（wi（j））m×n；

（3）分别取α＝1、2，p＝1、2的4种组合按式（12）计算样本j的相对优属度；

（4）对4种组合相对优属度值求平均，得相对优属度向量；

（5）按值从大到小的顺序排序即得指标特征值矩阵的排序；

（6）结束.

2 应用研究

为验证模型的有效性，将评价结果与DEA结果、文献［12］中建立的相对距离模型和文献［19］中TOPSIS模型结果进行对比分析，结果见表3.其中sj表示样本点相对理想点的距离变量，s＊j为样本点与理想点距离，s－j为样本点与非理想点距离，c＊j为样本点与最理想点的相对接近度.

各模型对比分析结果如下：

首先，DEA 可以看作是处理多输入多输出问题的多目标决策方法［13］.评价中可能出现多个目标同时达到有效的状态，不利于决策者选择.如算例中除样本4为最劣样本外，其余样本均达到效率值为1的最优样本的条件.本文算法根据DEA生成的客观权重进行再评价，在模型的4种组合下均产生唯一排序，最劣样本与DEA 算法一致.

其次，可变模糊模型中要求在评估前人为确定各指标权重，采用主观赋权的方法，各项指标权重之和为一，即不同于主观赋权所采用的专家经验，本文算法在权重的求解与计算方面根据样本数据特点挖掘数据指标间存在的客观关系，分析出样本集合中处于相对最优情况的样本个体，利用数学规划的手段在Pareto有效前沿下生成客观权重矩阵，放宽了可变模糊模型中指标权重之和为一的约束条件.

第三，应用TOPSIS算法对样本进行排序.由于文献［19］所采用的数据规格化公式不同于本文，为增加排序结果的可对比性，降低数据规格化方式不同对最终排序造成的影响，本文对样本原始数据采用相同的规格化公式，即式（4）～（5）重新计算，计算流程及理论分析如文献［19－20］所述.所用专家指标权重依次为0.001 0、0.001 0、0.325 4、0.634 6、0.001 0、0.001 0.排序 的 结 果如表3后3 列所示.TOPSIS算法在样本数据较接近的情况下，理想点和非理想点向量所构成的中垂线上及靠近非理想点的中垂线部分，不同衡量标准下样本点排序存在不合理的现象［20］.易见s＊j、s－j的排序存在差别，除样本3、4、5外均不能同时满足“距离理想点越近越优”和“距离非理想点越远越优”的一致性条件，最大的排序偏差发生在样本7，按s＊j排序第5，按s－j排序第1.最终排序是前两种排序的折中排序，最优样本为样本10.

当α＝1，p＝2时，可变模糊模型具体化为TOPSIS模型，因此二者存在的具体差别在于权重的确定.从识别最优样本的角度考虑，本文算法基于客观权重计算样本10 为最优样本，与TOPSIS专家权重产生的最优样本结果一致，证明了客观权重的可适用性.因此能够适用于由于事前信息量不足而造成的专家权重难以确定或专家意见不统一的情况.

表1 10辆汽车的6项指标数据Tab.1 Data for ten cars with six criteria

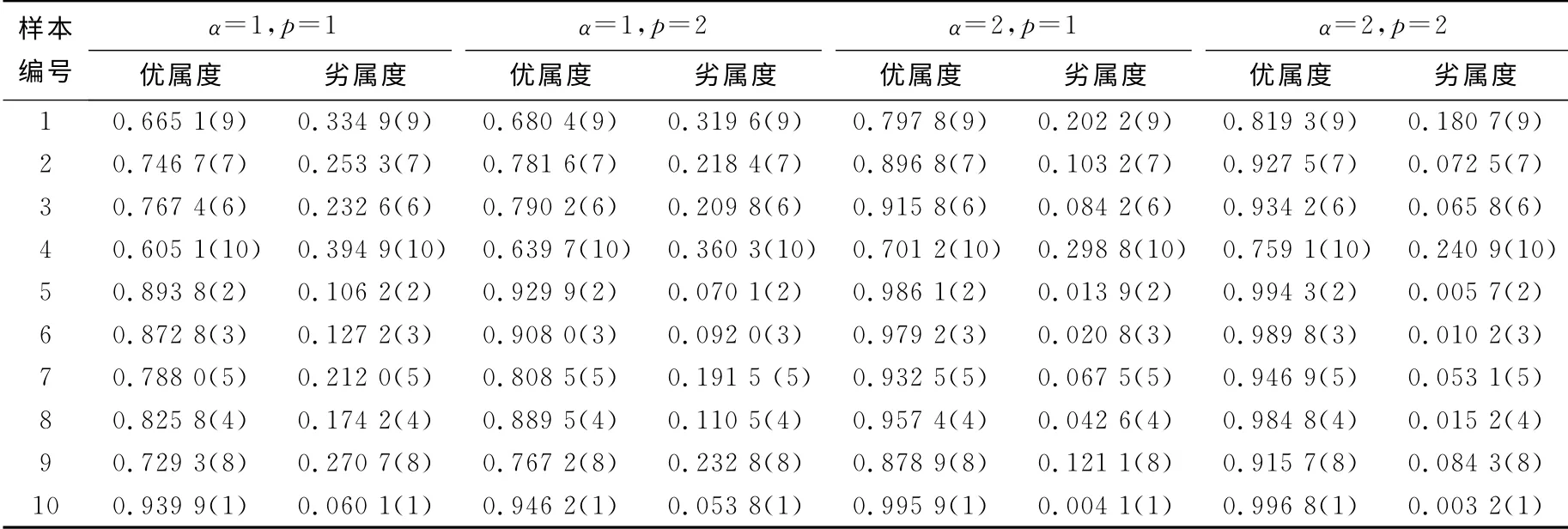
表2 可变模糊决策模型相对优属度计算结果Tab.2 Relative optimal membership degrees of variable fuzzy decision－making model

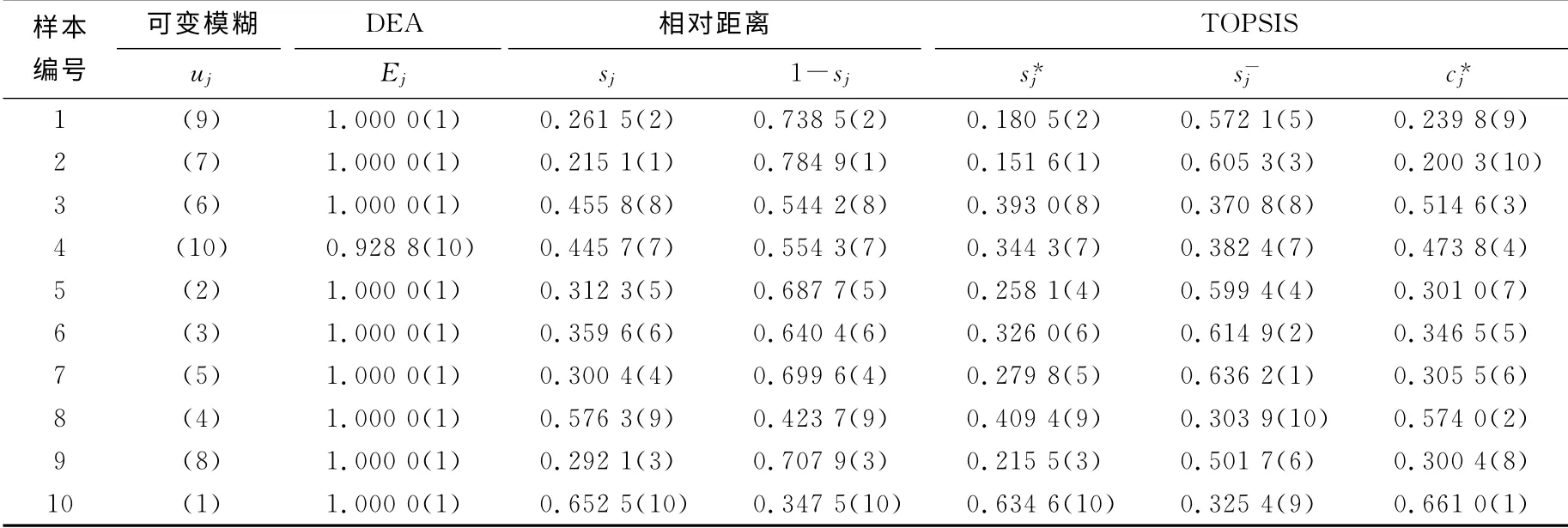
表3 可变模糊、DEA、相对距离、TOPSIS模型的汽车排序结果Tab.3 Ranking for the car example from the variable fuzzy，DEA，relative distance，TOPSIS models

最后，同文献［12］中建立的相对距离模型进行比较分析.相对距离模型的原理为根据DEA模型生成客观权重，在此基础上引入相对距离的思想，刻画样本点和理想点之间的相对差异，并根据此差异生成最终的样本排序.因此，在对最优、最劣样本的识别上应与DEA 模型产生的排序结果保持一致.从数据结果可以看出，相对距离模型满足了理想点与非理想点距离之和为一的要求，但其排序却不能与DEA 模型排序结果相符，如DEA 模型下，样本4排序第10，相对距离模型中样本4排序第7.其次，该模型所用为原始数据，未进行规格化处理.由于样本数据可能存在较大的离散型，导致规划求解难以满足wi＞ε的条件，因此模型在约束中增加了理想点与非理想点的比例系数b，即wi（Y＊i－Y－i）＝b.然而，比例系数b的设定需要人为主观确定，在建模思想上与该相对距离模型利用数据生成客观权重的思想不统一.

3 结 论

本文采用客观赋权的方法，从多个指标中寻找使目标样本趋于最优的权重集合，并利用可变模糊集合理论的对立统一思想对样本进行计算排序.该模型解决了DEA 评价结果不唯一的问题.

在可变模糊模型中引入DEA 客观权重，权重的计算基于样本数据不同指标的综合表现.首先，在DEA 计算生成的客观权重矩阵下，可变模糊的4种不同组合模型能够产生一致排序.客观权重矩阵的引入放宽了可变模糊模型中对权重之和为1的约束条件，算例结果证明客观权重矩阵能够应用于可变模糊模型.其次，4组模型的相对优属度和相对劣属度排序结果在“距离理想点越近越优”和“距离非理想点越远越优”两个标准下分别产生相同的排序结果，且二者之和为1，故模型适用于决策者无法确定优选衡量标准的情况.第三，TOPSIS算法是可变模糊模型取α＝1，p＝2时的特例，从择优的角度出发，应用客观权重的可变模糊方法和应用主观权重的TOPSIS方法能够识别出相同的最优样本.在这一特点下，考虑权重客观度的可变模糊多目标决策模型更适用于决策偏好信息不完全或专家意见不统一时所导致的权重标准难以确定的情况.最后，客观赋权法的决策或评价结果相对比较合理、客观，可操作性和实用性强.综上所述，此法为解决偏好信息不完全下的多目标决策问题提供了一条新的途径.

［1］ 饶从军，肖新平.多目标决策问题的模糊数学解法［J］.武汉理工大学学报：交通科学与工程版，2006，30（4）：700－703.RAO Cong－jun，XIAO Xin－ping.Method for the problem of multi－objective decision making based on fuzzy math theory［J］.Journal of Wuhan University of Technology：Transportation in Science ＆Engineering，2006，30（4）：700－703.（in Chinese）

［2］ Zeleny M.Multiple Criteria Decision Making［M］.New York：McGraw－Hill，1982.

［3］ 徐克龙.两两比较的TOPSIS法［J］.数学的实践与认识，2010，40（5）：110－114.XU Ke－long.TOPSIS method based on pairwise comparisons ［J］.Mathematics in Practice and Theory，2010，40（5）：110－114.（in Chinese）

［4］ 徐泽水.语言多属性决策的目标规划模型［J］.管理科学学报，2006，9（2）：9－17.XU Ze－shui.Goal programming models for multiple attribute decision making under linguistic setting［J］.Journal of Management Sciences in China，2006，9（2）：9－17.（in Chinese）

［5］ 许丽忠，张江山，王菲凤.熵权多目标决策环境监测优化布点模型及应用［J］.环境工程，2007，25（1）：61－63.XU Li－zhong，ZHANG Jiang－shan，WANG Feifeng.Optimization of environmental monitoring sites by entropy weight multi－object decision model［J］.Environmental Engineering，2007，25（1）：61－63.（in Chinese）

［6］ 徐泽水.部分权重信息下多目标决策方法研究［J］.系统工程理论与实践，2002，1（1）：43－47.XU Ze－shui.One method for multi－objective decision－making with partial weight information［J］.Systems Engineering－Theory ＆Practice，2002，1（1）：43－47.（in Chinese）

［7］ YU P L.A class of solutions for group decision problems［J］.Management Science，1973，19（8）：936－946.

［8］ Jahanshahloo G R，Afzalinejad M.A ranking method based on a full－inefficient frontier ［J］.Applied Mathematical Modeling，2006，30（3）：248－260.

［9］ 费 奇，刘敬学.一种基于模糊偏好信息的多属性决策方法［J］.武汉理工大学学报，2006，28（9）：132－140.FEI Qi，LIU Jing－xue.A multi－attribute decision making method based on fuzzy preference information［J］.Journal of Wuhan University of Technology，2006，28（9）：132－140.（in Chinese）

［10］ 双 晴，袁永博，双 凯.基于改进数据包络分析的建设工程评标模型［J］.数学的实践与认识，2012，42（8）：9－15.SHUANG Qing，YUAN Yong－bo，SHUANG Kai.A new method for construction engineering bidding evaluation［J］.Mathematics in Practice and Theory，2012，42（8）：9－15.（in Chinese）

［11］ Charnes A，Cooper W W，Rhodes E.Measuring the efficiency of decision making units ［J］.European Journal of Operational Research，1978，2（6）：429－444.

［12］ KAO Cao.Weight determination for consistently ranking alternatives in multiple criteria decision analysis ［J］.European Journal of Operational Research，2010，34（7）：1779－1787.

［13］ 魏权龄，岳 明.DEA 概论与C2R 模型——数据包络分析（一）［J］.系统工程理论与实践，1989（1）：58－69.WEI Quan－ling，YUE Ming.An introduction to DEA and C2R model －Data envelopment analysis（1）［J］.Systems Engineering－Theory ＆ Practice，1989（1）：58－69.（in Chinese）

［14］ Zadeh L A.Fuzzy sets ［J］.Information and Control，1965，8（3）：338－353.

［15］ 陈守煜.可变模糊集理论哲学基础［J］.大连理工大学学报：社会科学版，2005，26（1）：53－57.CHEN Shou－yu.Philosophical foundation of variable fuzzy sets theory ［J］.Journal of Dalian University of Technology：Social Sciences，2005，26（1）：53－57.（in Chinese）

［16］ 陈守煜.工程可变模糊集理论与模型——模糊水文水资源学数学基础［J］.大连理工大学学报，2005，45（2）：308－312.CHEN Shou－yu.Theory and model of engineering variable fuzzy set— Mathematical basis for fuzzy hydrology and water resources ［J］.Journal of Dalian University of Technology，2005，45（2）：308－312.（in Chinese）

［17］ 陈守煜.工程模糊集理论与应用［M］.北京：国防工业出版社，1998.CHEN Shou－yu.Engineering Fuzzy Set Theory and Application［M］.Beijing：National Defense Industry Press，1998.（in Chinese）

［18］ 陈守煜.可变模糊集理论与模型及其应用［M］.大连：大连理工大学出版社，2009.CHEN Shou－yu.Theory and Model of Variable Fuzzy Sets and Its Application［M］.Dalian：Dalian University of Technology Press，2009.（in Chinese）

［19］ Jacquet－Lagrèze E，Siskos J.Assessing a set of additive utility functions for multiple criteria decision making ［J］.European Journal of Operational Research，1982，10（2）：151－164.

［20］ 胡永宏.对TOPSIS法用于综合评价的改进［J］.数学的实践与认识，2002，32（4）：572－575.HU Yong－hong.The improved method for TOPSIS in comprehensive evaluation ［J］.Mathematics in Practice and Theory，2002，32（4）：572－575.（in Chinese）