复合钢板对GFRP箱梁性能影响

李耘宇，王言磊，欧进萍

（大连理工大学 土木工程学院，辽宁 大连 116024）

0 引 言

钢材和混凝土是目前建筑、桥梁等结构中使用的主要材料.近年来，钢筋混凝土结构和钢结构的腐蚀、劣化问题日益严重，其中以钢材锈蚀最常见，这不仅影响结构的正常使用和寿命，还造成大量的安全和事故隐患［1］.因此，减少和避免钢材锈蚀对工程结构造成的不利影响已成为急需解决的问题.采用耐腐蚀的新型结构材料——纤维增强复合材料（fiber reinforced polymer，FRP）是一种很好的解决途径［2］.FRP 以其比强度高、比模量大、耐腐蚀和抗疲劳等特点在土木工程中已得到越来越多的重视［3－4］.

然而，纯FRP 存在弹性模量低（尤其GFRP）、剪切模量小、脆性破坏和价格高等缺点.钢材却具有弹性模量高、剪切模量大、延性好和价格低等优点，但同时钢材还有强度低、自重大、易锈蚀等缺点.由上可知，FRP 与钢材具有极强的互补性，将FRP 与钢复合，能扬长避短、优势互补.一般GFRP 箱梁设计的控制指标是刚度，为了提高GFRP箱梁的刚度，可在GFRP箱梁中复合钢板，即为GFRP／钢复合箱梁；由于CFRP 的弹性模量也远大于GFRP，复合单向CFRP 同样也能有效提高整个截面的抗弯刚度.因此，可以在GFRP箱梁中以相同方式复合单向CFRP，即为GFRP／CFRP复合箱梁.

为了考察复合钢板后钢板体积比（复合部位钢板体积与总体积之比）对GFRP箱梁性能的影响，本文将以某一特定GFRP 箱梁为例，通过理论计算的方法，分析在GFRP箱梁中以不同方式复合钢板后钢板体积比对GFRP 箱梁性能的影响，同时对比分析在GFRP 箱梁中复合单向CFRP的情况，为进一步深入研究GFRP／钢复合箱梁性能提供一定的参考.

1 GFRP／钢复合箱梁特性

在GFRP 箱梁中复合钢板或单向CFRP 的方式是多样的：可在GFRP箱梁上下翼缘中复合钢板，以提高梁的整体刚度，如图1（a）所示；同时GFRP箱梁腹板的抗剪模量和抗剪强度一般也都比较低，为提高其抗剪能力，还可在GFRP 箱梁的腹板中也复合钢板，如图1（b）所示.类似地，可在箱梁上下翼缘中以相同方式复合单向CFRP，以提高其整体刚度，如图1（a）所示.

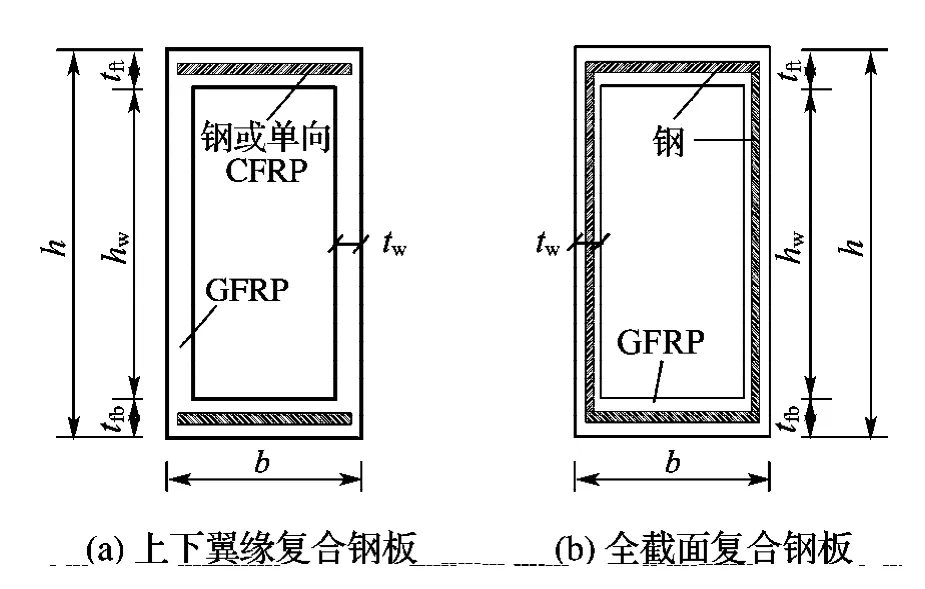
图1 GFRP／钢复合箱梁截面示意图Fig.1 Cross－section of GFRP／steel composite box beams

1.1 GFRP箱梁尺寸与材料特性

为了考核复合钢板后钢板体积比对GFRP箱梁性能的影响，本文选取某一特定GFRP 箱梁，箱梁截面如图1所示，梁高h＝300mm，梁宽b＝150mm，箱梁计算跨径L＝3 000mm，腹板厚度tw＝8mm，腹板高度hw＝276 mm，上下翼缘厚度相等（此时截面刚度最大），即tft＝tfb＝12 mm，为单跨简支梁.在保持箱梁截面尺寸不变的条件下，计算分析复合钢板或单向CFRP 对箱梁性能的影响.考虑到GFRP／钢复合型材的成型工艺与复合体材料间的受力协调等因素，钢板体积比或单向CFRP体积比（复合处单向CFRP体积与总体积之比）不宜大于50%.文中钢材选用Q345钢，单向CFRP 是由标准型（T300）碳纤维按45%的体积比与乙烯基酯树脂复合而成的.复合箱梁中各材料的性能参数分别见表1、2.文中钢板与GFRP复合后的材料性能参数，是按照经典层合板理论进行计算的（将钢板认为是特殊正交各向异性材料），这样GFRP／钢复合板也是正交各向异性材料.

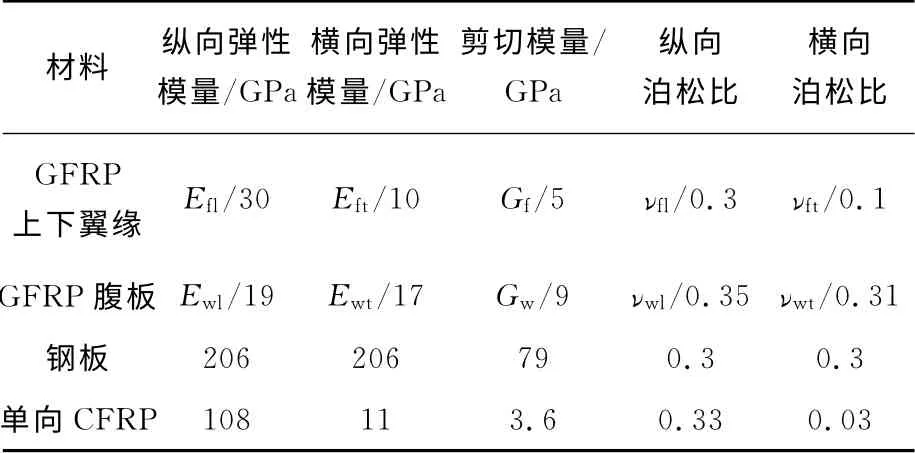
表1 材料特性Tab.1 Material properties

表2 材料密度和参考价格Tab.2 Material densities and reference prices

对于拉挤成型的FRP 材料（纤维体积比较高），其应力－应变关系接近于线弹性.钢材的应力－应变关系可简化为理想弹塑性模型.在FRP板中复合钢板后，FRP／钢复合板的应力－应变关系将会呈现如图2所示的双线性特征：在钢板屈服之前，复合板的刚度较大（FRP 与钢板同时提供刚度），应力－应变关系呈线性变化；钢材屈服之后，复合板的刚度明显下降（仅FRP 提供刚度），其应力－应变关系仍呈线性.称钢板屈服后复合板的刚度为二次刚度，可见FRP／钢复合板具有稳定的二次刚度.稳定的二次刚度能够控制地震或者超载情况下结构的变形，减小结构的残余变形，提高结构的可修复性［5－7］.

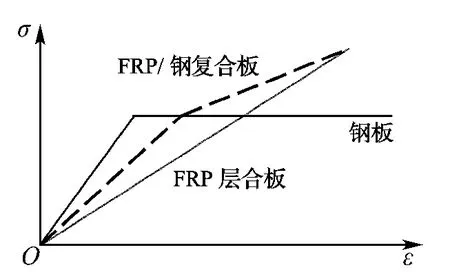
图2 材料模型Fig.2 Material model

1.2 GFRP箱梁的相关计算公式

结构工程中所用GFRP 材料一般为正交各向异性材料，其相关的计算公式与各向同性材料有很大的不同.下面简单介绍一下本文涉及的相关计算公式.

（1）GFRP箱梁上翼缘受压屈曲

在弯曲荷载作用下，GFRP 箱梁可能发生多种失效模式，为简化分析，本文仅考虑上翼缘受压屈曲这一种失效模式.假设GFRP箱梁失效前一直处于弹性阶段，则根据材料力学公式σ＝My／I，其抗弯承载力

式中：y为中性轴到截面上边缘的距离，Ift为换算截面惯性矩，σcr为受压屈曲临界应力［8］，其表达式分别如下：

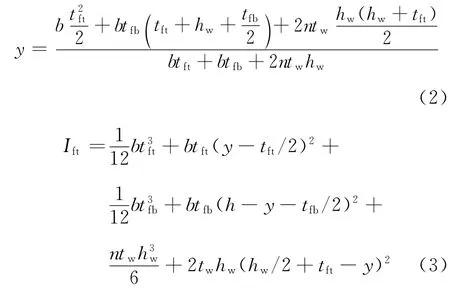
其中n＝Ewl／Efl.

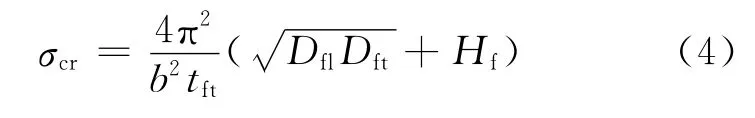
式中

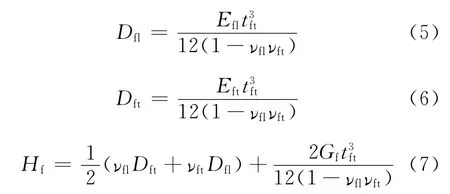
（2）GFRP箱梁腹板受剪屈曲

腹板受剪屈曲应力τbw与参数θ有关，其计算公式［8－9］为

若θ＞1

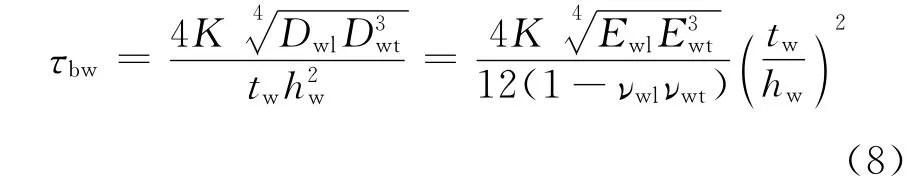
若θ＜1

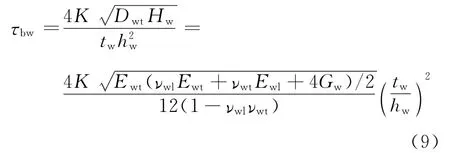
式中

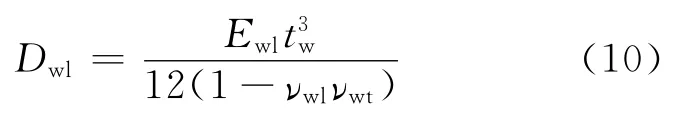
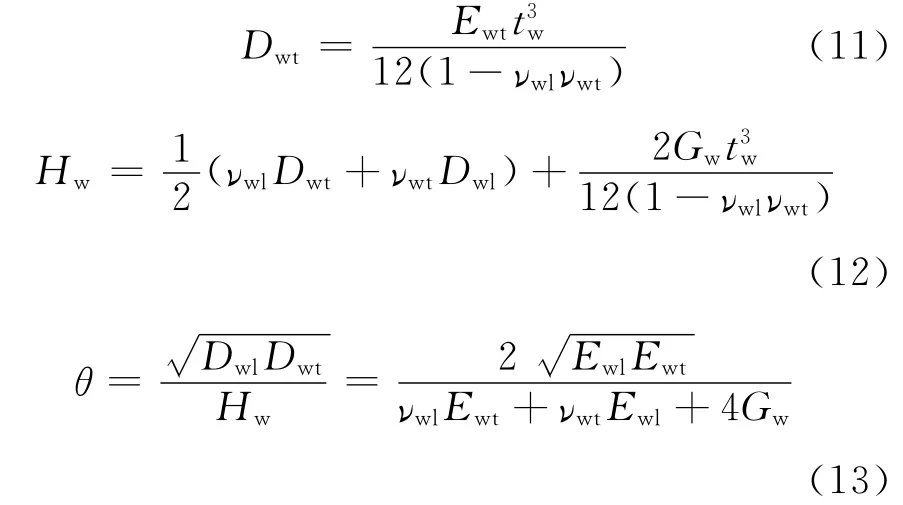
上述式中各个符号意义见图1和表1.

K是与θ有关的参数，对于两端固支无限长板，可由表3插值得出.

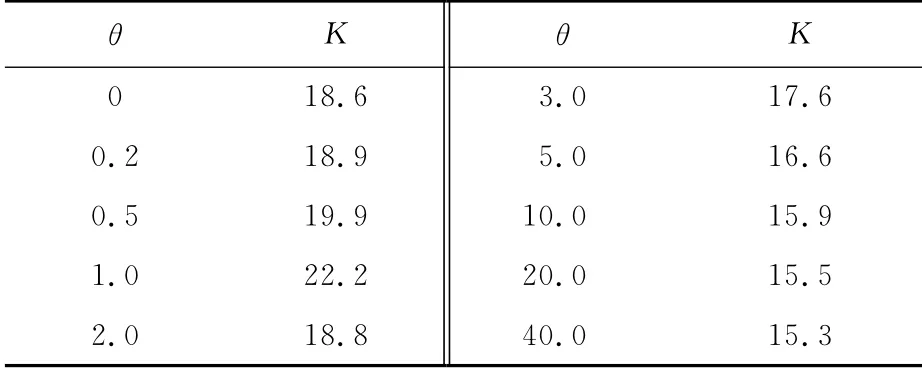
表3 K 的取值Tab.3 Values of K

此外，对于GFRP 结构，由于其剪切模量一般比较低，剪切变形在总变形中往往占有较高的比例而不容忽略.因此，GFRP箱梁的变形将由弯曲变形和剪切变形两部分组成［2］.

2 复合钢板对GFRP箱梁性能的影响

2.1 GFRP箱梁上下翼缘复合钢板

为了最大限度地提高箱梁的刚度，按上下翼缘等体积比复合钢板.在GFRP／钢复合箱梁设计中，复合钢板体积比Vs是一个关键的设计参数.增加钢板用量会增大截面刚度，同时减少GFRP的用量，但其自重也会增加.以下通过5 项指标（x）来考察钢板体积比变化对箱梁性能的影响：抗弯刚度（纵向）、抗弯承载能力（仅考虑上翼缘受压屈曲一种失效模式）、自重、造价、造价抗弯刚度比（造价与抗弯刚度之比）.图3显示了这5项指标的影响曲线（基于纯GFRP 箱梁的规则化结果），图中钢板体积比Vs从0变化到0.5.

从图3可以看出，随着钢板体积比的增大，箱梁的抗弯刚度、抗弯承载力和自重都呈线性增加，其中抗弯承载力的增长最为明显（当Vs＝0.5时，增长为原来的7倍左右），其增长率远大于抗弯刚度和自重的增长率，同时抗弯刚度的增长率（当Vs＝0.5时，增长为原来的3 倍左右）大于自重的，此时价格略有下降，造价抗弯刚度比也在逐渐下降.据此可知，钢板体积比越大，箱梁性能越优异，且造价几乎保持不变.

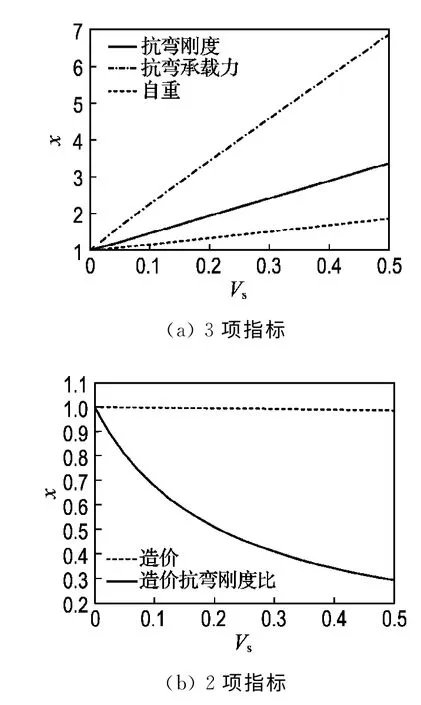
图3 钢板体积比对GFRP箱梁性能的影响Fig.3 Effects of steel volume ratio on the performance of GFRP box beam

2.2 GFRP箱梁上下翼缘复合单向CFRP

为了与复合钢板的模式相对比，同样在GFRP 箱梁上下翼缘中等体积比复合单向CFRP.此时，变化参数为单向CFRP 体积比Vcf，采用与上述2.1 相同的5 项指标来考核单向CFRP体积比变化对箱梁性能的影响.图4显示了这5项指标的影响曲线（基于纯GFRP箱梁的规则化结果），图中单向CFRP 体积比Vcf从0变化到0.5.

由图4中可知，随着单向CFRP体积比的增大，抗弯刚度呈线性增加，抗弯承载力稍有提升，同时自重呈线性减小，但变化不大，而造价却呈线性增长，且造价抗弯刚度比逐渐增大.由上可知，单向CFRP 体积比越大，箱梁抗弯刚度越大，但同时造价也会大幅提升，且造价提升的幅度大于抗弯刚度增加的幅度.

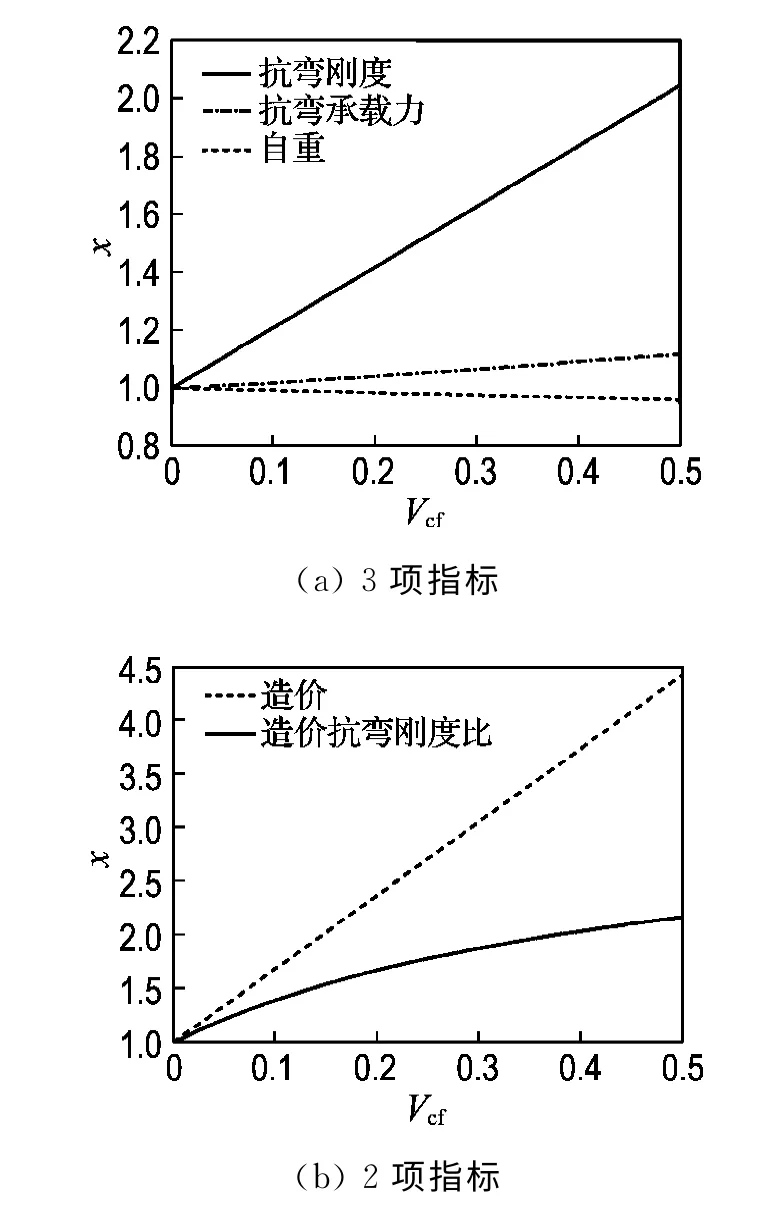
图4 单向CFRP体积比对GFRP箱梁性能的影响Fig.4 Effects of unidirectional CFRP volume ratio on the performance of GFRP box beam

2.3 GFRP 箱梁上下翼缘复合钢板与复合单向CFRP的对比

图3和4 分别给出了复合钢板和复合单向CFRP后，钢板体积比和单向CFRP 体积比变化对箱梁性能影响的趋势.为了更直观，现将二者放在一起进行比较，其对比曲线如图5所示.

图5表明，随着复合体积比的增大，上下翼缘复合钢板的抗弯刚度和抗弯承载力的增长率均大于复合单向CFRP的.同时复合钢板的自重增长较快，造价略有下降，而复合单向CFRP 的自重呈略微下降趋势，但造价却大幅度增加.复合单向CFRP的造价增长比较快，这就直接导致了在造价抗弯刚度比这个指标上，复合单向CFRP 的呈上扬趋势，而复合钢板的却呈下降趋势.由此可见，复合钢板和单向CFRP 均能使GFRP箱梁性能得到提高，但复合单向CFRP 的造价明显高于复合钢板的.综合比较，复合钢板要优于复合单向CFRP.

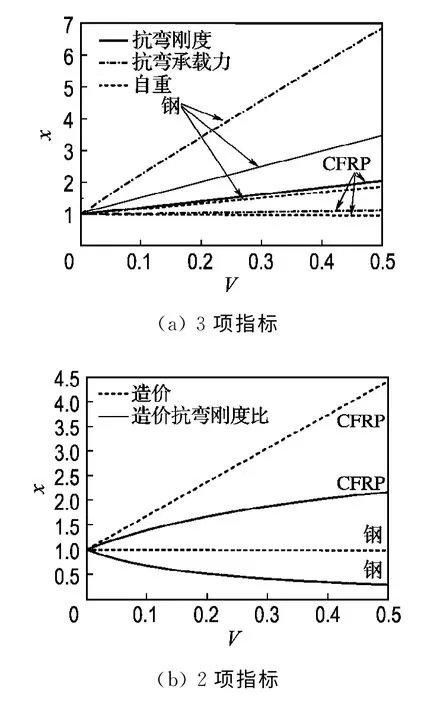
图5 钢板体积比与CFRP 体积比对GFRP箱梁性能的影响Fig.5 Effects of steel volume ratio and CFRP volume ratio on the performance of GFRP box beam

2.4 GFRP箱梁腹板复合钢板

如前所述，为了提高腹板的抗剪能力，在GFRP箱梁腹板中复合抗剪能力强的钢板.同样，在GFRP箱梁的双腹板中等体积比复合钢板.采用以下7项指标来考察钢板体积比Vs变化对箱梁性能的影响：腹板抗剪刚度、腹板抗剪屈曲能力、抗弯刚度（纵向）、自重、造价、造价抗剪刚度比（造价与腹板抗剪刚度之比）、造价抗弯刚度比（造价与抗弯刚度之比）.图6显示了这7项指标的影响曲线（基于纯GFRP箱梁的规则化结果），图中钢板体积比Vs从0变化到0.5.

图6（a）显示，随着钢板体积比的增大，腹板抗剪刚度、腹板抗剪屈曲能力、箱梁抗弯刚度和自重都呈线性增长，其中抗剪屈曲能力的增长幅度（当Vs＝0.5时，增长为原来的6倍左右）和抗剪刚度的增长幅度（当Vs＝0.5时，增长为原来的5倍左右）较大，其增长率远高于另外两项指标的，且抗弯刚度的增长率与自重的相差不大.从图6（b）中可见，随着钢板体积比的增大，造价略有下降，造价抗剪刚度比和造价抗弯刚度比都在逐渐下降，且造价抗剪刚度比的下降幅度更大.由上可知，钢板体积比越大，箱梁性能越优异，尤其是腹板的抗剪性能最为突出，而造价几乎保持不变.

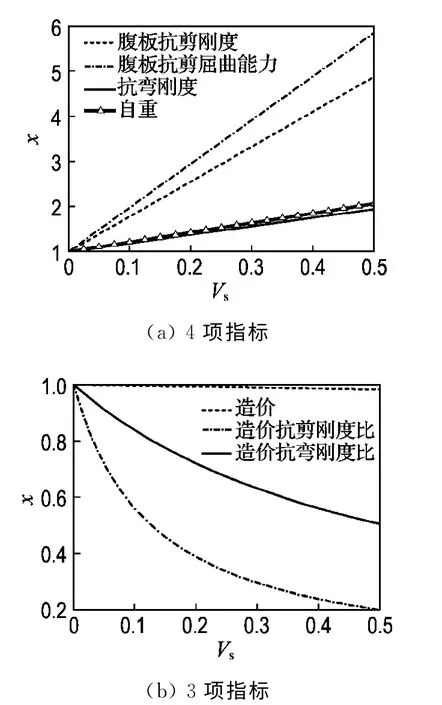
图6 腹板复合钢板体积比对GFRP箱梁性能的影响Fig.6 Effects of steel volume ratio in webs on the performance of GFRP box beam

2.5 GFRP箱梁全截面复合钢板

为了更好地考查全截面复合钢板（全截面等体积比复合钢板）时钢板体积比Vs对GFRP 箱梁抗弯性能的影响，下面将其与上下翼缘复合钢板的模式进行对比分析，采用与上述2.1中相同的5项指标进行考核.图7给出了这5项指标的对比曲线（基于纯GFRP箱梁的规则化结果）.

从图7（a）可见，随着Vs的增大，两种复合模式下的抗弯刚度、抗弯承载力和自重均呈线性增长，其中抗弯承载力的增长率最大，抗弯刚度的次之，自重的最小，同时全截面复合模式下的增长率明显高于上下翼缘复合模式下的.由图7（b）可知，随着Vs的增大，两种复合模式下的造价均略有下降，与之类似，造价抗弯刚度比也呈逐渐下降趋势，且全截面复合钢板模式下的下降率高于上下翼缘复合钢板模式下的.此外，如前面2.4 所述，全截面复合钢板模式下，GFRP腹板的抗剪性能会随Vs的增大而大幅提升.综上所述，钢板体积比越大，全截面复合模式下箱梁的性能越优，且造价几乎保持不变，另外，全截面复合钢板的性能明显优于上下翼缘复合钢板的.

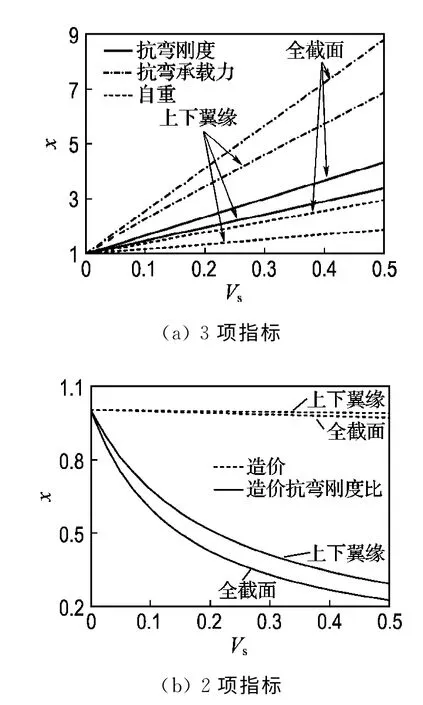
图7 上下翼缘和全截面复合钢板对比Fig.7 Comparing of adding steel plates into flanges and total cross－section

虽然全截面复合钢板模式下箱梁的性能最优异，但会大大增加其连续成型工艺的难度（如拉挤成型工艺等），实际加工起来会比较困难.而上下翼缘复合钢板模式，其连续成型工艺相对简单，且能大幅提升箱梁的抗弯性能，在实际工程中具有很好的应用前景.

3 结 论

（1）上下翼缘复合钢板和单向CFRP 模式下，复合体积比越大，箱梁的抗弯性能越优异，且复合钢板的性能提升幅度高于复合单向CFRP的，同时复合钢板的造价略有降低，而复合单向CFRP的造价却大幅提高，因此复合钢板要优于复合单向CFRP.

（2）腹板复合钢板模式下，钢板体积比越大，箱梁性能越优异，尤其是腹板的抗剪性能最突出，且造价几乎保持不变.

（3）全截面复合钢板模式下，钢板体积比越大，箱梁的性能越优秀，且造价几乎保持不变，同时全截面复合钢板的性能明显优于上下翼缘复合钢板的.

［1］ 陈肇元.土建结构工程的安全性与耐久性［M］.北京：中国建筑工业出版社，2003：1－6.CHEN Zhao－yuan.Safety and Durability of Structural Works in Civil Engineering［M］.Beijing：China Architecture and Building Press，2003：1－6.（in Chinese）

［2］ 王言磊.FRP－混凝土组合梁／桥面结构试验、分析与设计方法［D］.哈尔滨：哈尔滨工业大学，2008.WANG Yan－lei.Experimental investigation，analysis and design methods for FRP－concrete composite beam／bridge superstructure systems［D］.Harbin：Harbin Institute of Technology，2008.（in Chinese）

［3］ Bakis C E.Fiber－reinforced polymer composites for construction－state－of－the－art review［J］.Journal of Composites for Construction，2002，6（2）：73－87.

［4］ CHEN D，El－Hacha R.Hybrid FRP－concrete structural member：research and development in North America ［C］／／ Proceedings of the 5th International Conference on FRP Composites in Civil Engineering （CICE 2010）.Beijing：Tsinghua University Press，2010：185－190.

［5］ 雷 云.混杂FRP－RC 组合梁抗弯性能试验研究［D］.南京：东南大学，2009：69－71.LEI Yun.Experimental study on bending performances of hybrid FRP－reinforced concrete composite beams ［D ］.Nanjing：Southeast University，2009：69－71.（in Chinese）

［6］ 张 普，朱 虹，孟少平，等.混杂FRP－混凝土T 形组合梁受弯性能试验研究［J］.东南大学学报：自然科学版，2009，40（3）：548－553.ZHANG Pu，ZHU Hong，MENG Shao－ping，et al.Experimental study on bending performances of hybrid FRP－concrete composite T－beams ［J］.Journal of Southeast University：Natural Science Edition，2009，40（3）：548－553.（in Chinese）

［7］ 张 普，朱 虹，孟少平，等.FRP片材增强钢筋混凝土梁刚度与变形计算［J］.建筑结构学报，2011，32（4）：87－94.ZHANG Pu，ZHU Hong，MENG Shao－ping，et al.Calculation of sectional stiffness and deflection of FRP sheets strengthened reinforced concrete beams［J］.Journal of Building Structures，2011，32（4）：87－94.（in Chinese）

［8］ Holmes M，Just D J.GRP in Structural Engineering［M］.London：Applied Science Publishers Ltd.，1983：263－268.

［9］ Timoshenko S P，Gere J M.弹性稳定理论［M］.张福范，译.北京：科学出版社，1965.Timoshenko S P，Gere J M.Theory of Elastic Stability［M］.ZHANG Fu－fan，tran.Beijing：China Science Press，1965.（in Chinese）