G型结构立式镗铣机床位置刚度数值模拟与试验

孙永平，王德伦，马雅丽，董惠敏

（大连理工大学 机械工程学院，辽宁 大连 116024）

0 引 言

立式镗铣机床位置刚度是指主轴与工作台在单位荷载下误差敏感方向的变形量［1］，其决定了刀具寿命、切削颤振、机床加工精度等［2］，已成为制约立式镗铣机床加工精度的关键［3］.然而，机床主轴与工作台变形微小［4］，刚度试验平台难以进行复杂空间刚度性能测试，因此可通过数值模拟方法获得立式镗铣机床空间位置刚度分布规律.

目前，机床设计主要依赖于类比与经验设计方法，在装配调试过程中按照直线度、垂直度等几何精度检验允差进行装配［5］.国内外针对不同机床已进行了大量研究，但基于机床位置刚度的精密机床设计仍不成熟.Alexander采用坐标变换建立空间变形模型，可进行机床各功能组件、单元空间变形计算［6］；Koenigsberger采用集中质量法［7］将机床构件简化为弹簧和集中质量对龙门铣床进行变形计算，该方法无法考虑不同内部结构及联接单元对整机变形的影响，误差较大；Huang等［8］采用有限元分析方法对不同网格的立式加工中心部件刚度进行计算，提高了精度，但没有对机床各联接变形进行研究；Altintas等［9］采用弹簧简化丝杠、导轨进行立式加工中心静态性能数值模拟，忽略了主轴轴承影响；刘悦等［10］兼顾主轴轴承及直线导轨与滑块的接触刚度，采用有限元方法计算中心位置并联机床三向整机刚度，忽略了丝杠联接影响，导致理论与试验最大误差达15%.

本文以离散点法试验研究G 型结构立式镗铣机床整机空间X、Y、Z三向静刚度；同时，在具有预紧荷载的主轴轴承、线性导轨及丝杠试验数据基础上根据动联接特征对其进行等效简化，建立立式镗铣机床实体模型，采用有限元法模拟机床试验离散点空间静刚度，分析静刚度不均匀分布的主要原因，并进行机床Z轴移动部件，X、Y轴移动部件及整机工作空间位置刚度数值模拟，以期为改进G 型机床结构及切削加工提供指导.

1 机床结构与静刚度

立式镗铣机床可用于板类、盘类、壳体类等精密零件的加工.机床由床身、立柱、主轴箱、滑鞍与工作台等部件组成，其附属配件为刀库、电器柜与液压泵等.其中，立柱与床身采用螺钉联接，主轴和丝杠分别采用轴承支撑；X、Y、Z直线运动子系统间采用导轨与丝杠联接.

如图1所示，立式镗铣机床的主体构型为G型开式链机构，床身为基架，主轴与工作台分别为两条链的末端执行构件.该结构优点［4］为开式链机构力环路较短，可便捷装配，机床工作空间较大.机床主要工况为铣削和镗削，其中Z向为铣削工况误差敏感方向，X、Y向为镗削工况误差敏感方向.机床沿X、Y、Z轴移动的位置误差将直接复映于被加工件.因此，需对机床X、Y、Z轴静刚度进行研究.

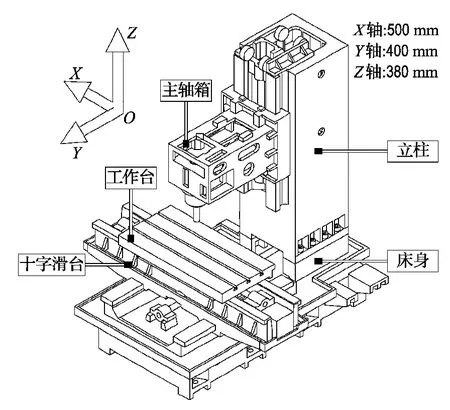
图1 立式镗铣机床结构及工作空间Fig.1 Structure and work space of vertical machine center

2 建模及数值模拟方法

2.1 联接单元等效

立式镗铣机床动联接单元主要包括回转轴承、直线轴承（丝杠、导轨）.其中，主轴固定端轴承承受轴向及径向负荷，支撑端只承受径向负荷；导轨承受径向和侧向荷载；丝杠主要承受轴向荷载.为增加机床刚性、减小间隙，各联接单元均增加预紧荷载，经试验验证机床静态情况下各动联接位移量相对负载呈线性变化，可根据滚动体数量进行简化，具体简化如表1所示.

表1 立式镗铣机床动联接单元等效Tab.1 Equivalence of the movable connections for vertical machine center

式中：Ka为轴向刚度，Kr为径向刚度，Kc为导轨侧向刚度，Kbai为单个轴承等效轴向刚度，Kbri为单个轴承等效径向刚度，Ksai为单个丝杠等效轴向刚度，Kgri为导轨径向刚度，Kgci为单个导轨等效侧向刚度.

2.2 网格划分及边界条件

机床采用程序控制网格分布，应用分块技术获得高质量网格：形状规则的块采用结构化的六面体网格，而结构复杂的块采用混合网格划分，最后得到高质量的四面体与六面体混合网格.

采用程序控制机床各动联接单元联接面处硬点的定义，并定义弹簧进行联接，共建立580组弹簧单元.在主轴模拟工件处施加设计荷载，全局施加重力；机床底端地脚螺栓施加全约束，支撑端施加Y向约束.表2为主要部件和弹簧材料的基本物理参数.

表2 材料基本物理参数Tab.2 Basic physical parameters of materials

3 数值模拟结果与分析

针对G 型结构立式镗铣机床180 个离散位置进行了数值模拟.机床在不同位置具有相应的位置刚度，切削时将复映为被加工零件的尺寸精度与位置精度.例如铣削工况产生平面度误差、镗削工况产生圆柱度误差.同时，G 型立式镗铣机床为开式链机构，主轴和工作台为末端执行构件，床身固定于基础平台，整机静刚度由主轴和工作台静刚度综合决定.下面依次对主轴、工作台及整机的空间静刚度进行研究.

3.1 Z 轴不同位置对主轴刚度的影响

机床主轴箱位于立柱不同行程坐标（180、220、260、300、340、380mm）处，对5个位置15种工况进行数值模拟，机床铣削、镗削误差敏感方向X、Y、Z向不同位置主轴静刚度分布曲线如图2所示.

从图2可以看出，主轴在Z轴坐标180 mm到380mm 处X向静刚度变化值为6.55N／μm、Y向静刚度变化值为20.84N／μm、Z向静刚度变化值为8.88N／μm.其中，机床主轴位于Z轴380 mm 处，X向静刚度最小为25.6N／μm.从中可以看出，G 型结构X向静刚度同Y、Z向相比较小，Y向静刚度变化最大；主轴在立柱底端移动至立柱顶端呈非线性递减变化规律.引起这种变化的主要原因是主轴箱体为G 型悬臂结构，当主轴箱体沿Z轴移动，立柱力传递路径变长，引起立柱弯曲扭转组合变形，导致主轴静刚度变化.主轴Z向静刚度呈S形变化主要是受立柱内部结构的影响.

3.2 X、Y 轴不同位置对工作台静刚度的影响

机床工作台位于X、Y轴不同行程，机床切削荷载作用点位置不同导致静刚度发生变化，图3为机床工作台在X、Y轴不同位置坐标的静刚度等值线分布图.

从图3中可以看出，在X轴与Y轴中间位置与边缘位置，工作台的静刚度变化较大.其中，工作台X向静刚度变化值为65.69N／μm，Y向静刚度变化值为54.35N／μm，Z向静刚度变化值为805.89N／μm，工作台从中间到边缘呈非线性递减变化规律.工作台静刚度最小位置为X轴和Y轴的极限坐标位置，其静刚度为70、55、112.5 N／μm，同立柱相比，工作台静刚度变化较大，主要是因为工作台导轨的离散点支撑，该结构是X、Y轴不同位置空间结构设计的薄弱环节.

3.3 平面内整机位置刚度空间分布

平面内整机位置刚度空间分布可表征被加工件的平面度.图4为机床精加工工况（Z轴位于180mm 处，X、Y轴在整个行程内）整机位置刚度分布的三维映射表面图.

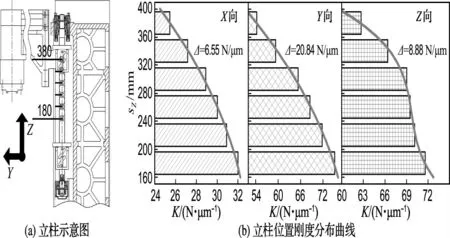
图2 立式镗铣机床立柱Z 向位置刚度分布曲线Fig.2 Curve of position stiffness of vertical machine center column in Zdirection

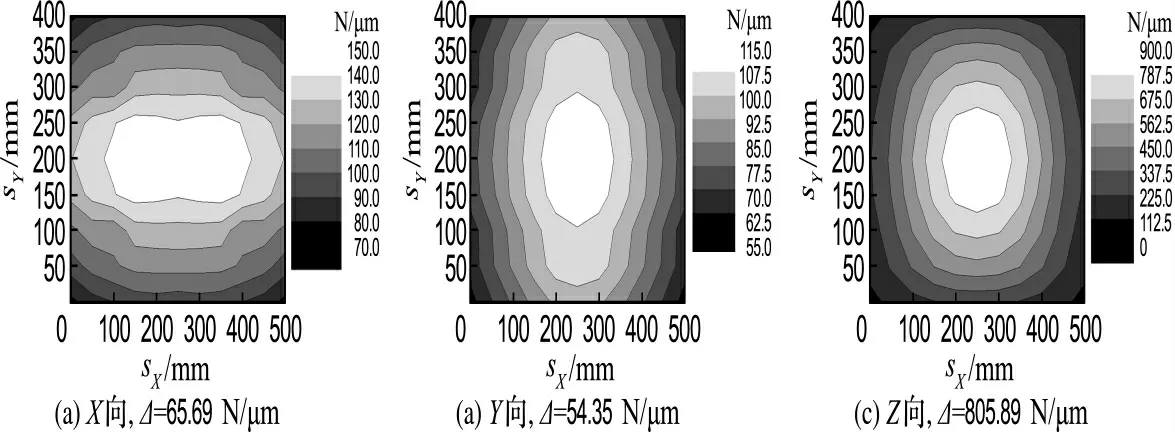
图3 工作台X、Y 轴静刚度等值线图Fig.3 Static stiffness isoline map of working table at Xaxis and Yaxis

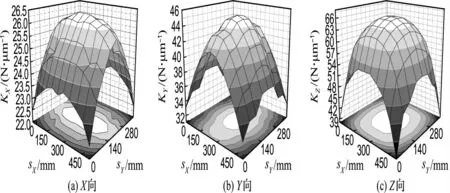
图4 整机空间静刚度分布三维映射表面图Fig.4 3－D map surface figure of static stiffness of complete machine

从图4可以看出，机床X、Y平面内不同坐标位置刚度呈鞍状变化，整机从中间到边缘呈非线性递减变化规律，中间位置刚度最大，边缘角点刚度最小.机床整机X、Y、Z向最大静刚度分别为26.35、45.29、66.24N／μm；边缘角点处静刚度最小为22.45、33.05、38.48N／μm.机床整机静刚度变化影响被加工表面几何精度，整机X向静刚度变化值为3.9 N／μm，Y向静刚度变化值为12.24N／μm，Z向静刚度变化值为27.76N／μm，加工大尺寸平面将产生较大平面度误差.同时，通过对比可以发现图4（a）和（b）形状类同，主要因为Z轴180mm 处主轴在X、Y、Z向静刚度变化量为32.00、75.12、71.58N／μm 固定不变，说明机床平面内几何误差主要由工作台刚度不均匀变化引起.

3.4 Z 轴移动整机位置刚度空间分布

G 型结构立式镗铣机床立铣、镗削等工况主轴箱体沿Z轴在立柱上移动，整机静刚度大小主要影响尺寸精度；整机静刚度变化值主要影响被加工件的圆柱度、垂直度等几何误差.通过计算得到了机床Z轴位置刚度，图5为主轴箱体沿Z轴移动整机位置刚度空间分布曲线.

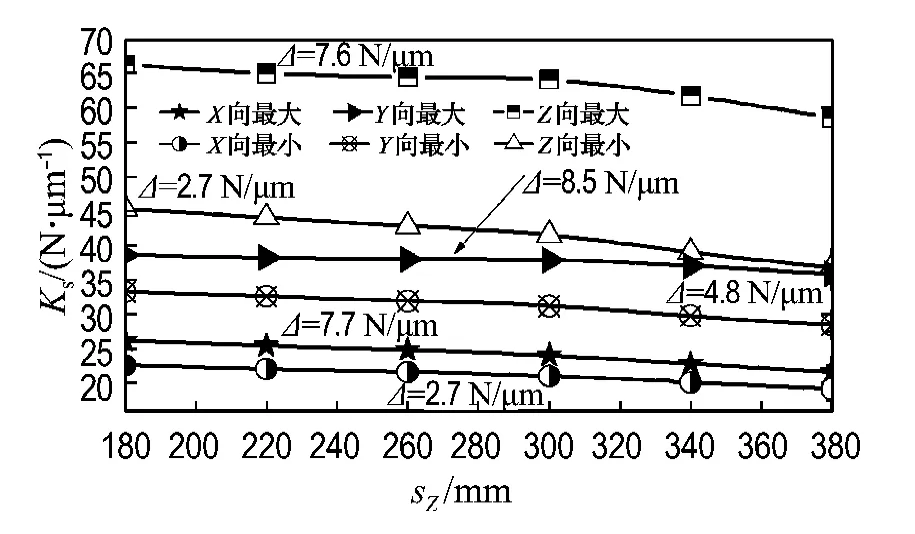
图5 Z 轴移动整机位置刚度空间分布曲线Fig.5 Spatial distribution curve of position stiffness of complete machine moving Zaxis

从分布曲线可以看出，整机X、Y向静刚度变化影响圆柱度，X向静刚度变化最大与最小分别为7.7、2.7N／μm；Y向的为8.5与4.8N／μm.整机Z向误差主要影响垂直度，Z向静刚度变化为7.6、2.7N／μm.

4 机床静刚度检测试验

4.1 试验仪器及条件

对机床X轴离散点坐标（50、100、150、200、250mm）（Y轴坐标150mm，Z轴坐标180mm）5个工况分别进行X、Y、Z三向整机静刚度试验.机床主轴回转轴承采用DB 排列，接触角度为15°，自由端预紧荷载为150 N、固定端为200 N［11］，机床动联接预紧荷载见表3［12－13］.

表3 立式镗铣机床直线轴承单元预紧载荷Tab.3 Preload of machine tools linear bearing unit of vertical machine center

试验采用力传感器进行荷载测量，分辨率为10N；光栅测位仪进行位移场测量，分辨率为0.1 μm；环境温度为（22±1）℃.

4.2 试验方案

机床静刚度试验在三向加载静刚度试验系统上进行，试验现场如图6所示.该试验平台由模拟工件1、加载装置2、测量系统3、测量基准支撑4四部分组成.模拟工件尺寸为215mm×215mm；加载装置采用螺杆微调进给进行荷载施加，荷载通过轮辐式力传感器显示，力传感器通过螺栓联接到模拟工件X、Y、Z三向，分辨率为100N；变形测量装置采用10通道接触式位移测量系统，光栅传感器分辨率为0.1μm；测量基准为自行设计的承载横梁组，通过螺栓联接于地基.

图6 立式镗铣机床静刚度试验测量系统Fig.6 Static stiffness measurement system of vertical machine center

试验测量了在不同荷载作用下，主轴和工作台三方向的变形量.通过光栅传感器分别测量主轴伸出端、模拟工件与工作台接触部分变形；施加荷载依次为400、800、1 200、1 600、2 000、2 400、2 800N7种荷载；测量时沿X、Y、Z三向加载卸载分别测量3次，取其平均值作为该次测量结果.由试验荷载和测量的位移可得立式镗铣机床在预紧荷载下的离散点静刚度值.为了验证数值计算结果的正确性，进行了试验结果与数值模拟结果比较.

4.3 试验结果与数值计算结果比较

对机床X轴移动，Y、Z轴固定共5个离散位置15个工况依次进行机床静刚度求解，求解结果同试验结果对比如图7所示.

图7 立式镗铣机床静刚度试验与数值模拟离散点对比Fig.7 Comparison of experimental and theoretical static stiffness at discrete points of vertical machine center

从图7中可以看出随着X轴坐标位置的变化，机床位置刚度呈弧形曲线变化，主要是由机床采用对称结构设计，工作台两端悬臂结构变形较大引起.机床试验结果比计算数值偏小，主要因为机床为复杂装配体，数值计算模型虽考虑了主要联接，并未考虑模拟工件与工作台（螺栓联接）等所有联接.同时，机床整机理论与试验X、Y、Z向最大残差分别为8.7%、8.5%、8.2%，数值模拟结果与试验结果较接近.

5 结 论

（1）根据动联接单元特征建立的立式镗铣机床静刚度模型，可进行机床整机静刚度测量，数值模拟结果与试验数据相比，最大误差为8.7%.

（2）G 型结构立式镗铣机床工作空间位置刚度随坐标变化而变化：随Z轴行程增加而非线性减小；X、Y轴中间位置刚度最大，呈抛物状向外递减，静刚度薄弱环节为工作台的支撑结构.

［1］ Weck M.Handbook of Machine Tools：Volume 2.Construction and Mathematical Analysis ［M］.London：Middlesex Polytechnic，1984.

［2］ Rivin E I.Trends in tooling for CNC machine tools：Machine system stiffness［J］.American Society of Mechanical Engineers Manufacturing Review，1991，4（4）：257－263.

［3］ 李圣怡.精密和超精密机床设计理论与方法［M］.长沙：国防科技大学出版社，2000.LI Sheng－yi.Design Theory and Method for Precision and Ultra－Precision Machine Tool［M］.Changsha：National University of Defence Technology Press，2000.（in Chinese）

［4］ Mekid S.Introduction to Precision Machine Design and Error Assessment ［M］.London：Taylor ＆Francis Group，2009.

［5］ 国家机械工业局.加工中心检验条件 第2部分：立式加工中心几何精度检验［S］.北京：中国标准出版社，1998.State Bureau of Machine－Building Industry.Test Conditions for Machining Centres－Part 2：Geometric Tests for Machines with Vertical Spindle ［S］.BeijingStandards Press of China1998.in Chinese）

［6］ Alexander H.Slocum，Precision Machine Design［M］.New Jersey：Prentice Hall，1992.

［7］ Koenigsberger F.Machine Tool Structures ［M］.London：Pergamon Press，1970.

［8］ Huang D T Y，Lee J J.Measured and predicted force and stiffness characteristic of industrial magnetic bearings ［J］.International Journal of Machine Tools and Manufacture，2001，41（8）：1149－1163.

［9］ Altintas Y，Brecher C，Weck M，etal.Virtual machine tool ［J］.CIRP Annals，Manufacturing Technology，2005，54（2）：115－138.

［10］ 刘 悦 汪劲松.基于轴承及导轨接触刚度的混联机床静刚度研究及优化［J］.机械工程学报，2007，43（9）：151－155.LIU Yue，WANG Jin－song.Static stiffness research and optimization on a hybrid machine tool considering the stiffnesses of bearings and guide ways ［J］.Chinese Journal of Mechanical Engineering，2007，43（9）：151－155.（in Chinese）

［11］ NSK.Linear Guideway ＆Ball Screws［Z］.Tokyo：NSK.Ltd.，2011.

［12］ Harris T A.Rolling Bearing Analysis ［M］.London：Taylor ＆Francis Group，2006.

［13］ NSK.Super Precision Bearings［Z］.Tokyo：NSK.Ltd.，2010.