求最小生成树的矩阵算法

毛 华， 史田敏， 高 瑞

(1．河北大学数学与计算机学院 河北 保定071002;2．沧州师范学院数学系 河北沧州061001)

0 引言

树是图论中一种重要的图类，是基尔霍夫在解决电路理论中求解联立方程时首先提出来的，可是他的发现超越了时代，因而长期没有引起重视［1－4］，然而伴随着现代科技的发展，现在树的概念已经越来越广泛地被应用，特别是最小生成树理论，已成为图论中的一支奇葩．常用的最小生成树的算法——破圈法和Kruskal算法［2－10］，算法过程中都需要在原有图上进行分析，不易使用计算机语言处理．另一著名的最小生成树算法——Dijkstra算法，虽然易于在计算机上实现，但是该算法的缺点是不易理解和掌握．基于以上3种算法，作者提出了一种新的求最小生成树的矩阵算法，此算法易于在计算机上实现，且易于理解和掌握．

1 预备知识

定义1［1－5］(1)不含圈的连通图称为树．

(2)如果T是G的一个生成子图，而且又是一棵树，则称T是图G的一棵生成树．生成树T中的边称为树枝．

(3)设G=(V，E)是连通的赋权图，T是G的一棵生成树，T的每个树枝所赋权值之和称为T的权，记为w(T)．G中具有最小权的生成树称为G的最小生成树．

引理1［1－5］图G有生成树的充要条件是G为连通图．

2 算法

2．1 算法的思想

设 G=(V，E，w)是一个简单的连通无向图，W 表示权矩阵，其中，wii=+∞，i=1，2，…，n;若 vivj∈E(G)，则 wij=w(vivj);若 vivj∉E(G)，则 wij=+∞．

设B=∅，B的基数为K(B)=0，D=∅．为了保证算法在无圈的基础上进行，先从W中找出任意一行的最小元，不妨设为 wij(i，j∈{1，2，…，n})．若{i，j}⊄D，则 B=B∪{vivj}，K(B)=K(B)+1，D=D∪{i，j}，此时用小括号在W中标记wij，wji;若{i，j}⊂D，则B=B，K(B)=K(B)，D=D，此时用中括号在 W 中标记 wij，wji．然后在W中选取D中元素对应行中除标记外的最小元，重复上述过程，直到K(B)=n－1，算法停止，B中的元素构成图G的一个最小生成树．

2．2 算法的步骤

Step 0 初始化B=∅，K(B)=0，D=∅．

Step 1 任选权矩阵W的某一行中的最小元，不妨设为wij(i，j∈{1，2，…，n})．

Step 2 若{i，j}⊄D，则 B=B∪{vivj}，K(B)=K(B)+1，D=D∪{i，j}，同时把权矩阵 W 中对应的 wij，wji用小括号做上标记;否则B=B，K(B)=K(B)，D=D，同时把权矩阵W中对应的wij，wji用中括号做上标记．若K(B)=n－1，算法停止，B的元素构成图G的一个最小生成树．

Step 3 在权矩阵W中选取D中元素对应行中的除标记外的最小元，转Step 2．

2．3 算法的复杂度分析

3 应用举例

下面通过一个实例说明，利用给出的算法得到所求的最小生成树．例 求解图G的最小生成树(图1)．解

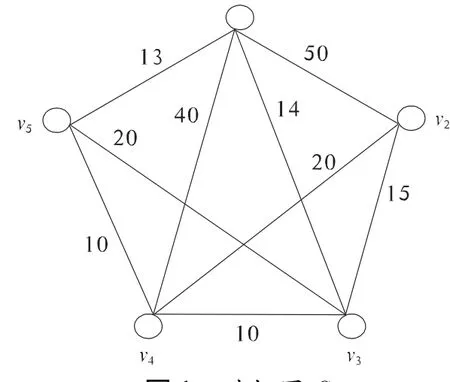
图1 赋权图GFig．1 Weighted graph G

构造一个关于赋权图G的n×n权矩阵W，令已选的边记为B=∅，K(B)表示已选边的个数，所选边的下标集记为D．

(1)不妨先从权矩阵W的第一行选起，选取权矩阵第一行的最小元为w15=13，此时{1，5}⊄D，B=B∪{v1v5}，K(B)=1，D=D∪{1，5}={1，5}，把权矩阵 W 中的 w15，w51用小括号做上标记．

(2)在权矩阵 W 中第1，5行中除标记外的最小元为 w54=10，{5，4}⊄D，B=B∪{v5v4}，K(B)=2，D=D∪{5，4}={1，4，5}，把权矩阵 W 中的 w54，w45用小括号做上标记．

(3)在权矩阵 W 中第1，4，5行中除标记外的最小元为 w43=10，{4，3}⊄D，B=B∪{v4v3}，K(B)=3，D=D∪{4，3}={1，3，4，5}，把权矩阵 W 中的 w43，w34用小括号做上标记．

(4)在权矩阵 W 中第1，3，4，5 行中除标记外的最小元为 w31=14，{3，1}⊂D，B=B，K(B)=K(B)，D=D，把权矩阵W中的w31，w13用中括号做上标记．

(5)在权矩阵 W 中第1，3，4，5 行中除标记外的最小元为 w32=15，{3，2}⊄D，B=B∪{v3v2}，K(B)=5 －1=4，D=D∪{3，2}={1，2，3，4，5}，算法停止．

最后 B={v1v5，v5v4，v4v3，v3v2}，所选的边 v1v5，v5v4，v4v3，v3v2构成所求最小生成树．

构成最小生成树边 v1v5，v5v4，v4v3，v3v2的复杂度为 O(3)，O(4)，O(6)，O(6)，选 w31的复杂度为 O(8)，所以整个算法复杂度为O(27)，与文中所提出的算法复杂度一致，故该算法有效．

4 结束语

最小生成树的知识在实际生活中有重要的应用，也是图论的重要组成部分．作者利用图的有关知识，为最小生成树问题提出新的算法，丰富了生成树的理论内容，此算法可以在做最小生成树时达到简单易懂之目的．在以后的工作中，将继续研究有向赋权图的最小生成树和最大流相关的各类问题．

［1］ Bondy J A，Murty U S R．Graph Theory with Applications［M］．New York:Elsevier Science Publishing Co Inc，1976:36 －101．

［2］ 谢政．网络算法与复杂性理论［M］．长沙:国防科技大学出版社，2003:1－50．

［3］ 王朝瑞．图论［M］．北京:北京理工大学出版社，2001:1－35．

［4］ 谢美萍．离散数学［M］．北京:清华大学出版社，2008:139－179．

［5］ 傅彦．离散数学常见题型解析及模拟题［M］．西安:西北工业大学出版社，2004:88－111．

［6］ 胡先富，李娜．格上传递矩阵的性质［J］．四川师范大学学报:自然科学版，2009，32(6):751－756．

［7］ 孙波，钟声．带匹配限制的交错路调课模型［J］．广西师范大学学报:自然科学版，2007，25(4):100－103．

［8］ 邓俊强，林诒勋．运输问题图上作业法的分解算法［J］．郑州大学学报:理学版，1994，26(6):9－16．

［9］ 毛华，谢利伟，张智星．基于剪枝的最小生成树算法在供水管网的应用［J］．计算机应用与软件，2011，28(2):109－110．

［10］聂玲，程涛．工件有工期并且可拒绝单机最小化最大提前时间的排序问题［J］．郑州大学学报:理学版，2012，44(3):42－45．