多部图的最大匹配算法

毛 华， 赵小娜, 史田敏， 毛晓亮， 刘 辉

(河北大学 数学与计算机学院 河北 保定 071002)

多部图的最大匹配算法

毛 华， 赵小娜, 史田敏， 毛晓亮， 刘 辉

(河北大学 数学与计算机学院 河北 保定 071002)

匹配理论是图论中一个重要的分支，已被广泛地应用于许多领域，如组合优化、线性规划、人工智能和矩阵论等.给出一个求解多部图的最大匹配算法，并用仿真例子说明其实用性和有效性，此算法为解决复杂的指派问题开辟了新途径.

匹配理论； 最大匹配； 多部图

0 引言

图论思想和方法越来越被许多科学领域所接受，并日益发挥它的重要作用.进入21世纪以来，图论又成为研究人员讨论的热点,特别是图论中的匹配知识在生产实践中有着重要的应用，多部图的匹配作用更是如此，在实际生活中的“工作安排”、“体育比赛”等都用到多部图匹配知识.另外，在“交巡警安排”、“铁路调度”、“公交调度”、“运营线路选择”和“飞机排班问题”等都有多部图的成功运用.此外，在知识发现、知识获取以及人工智能等方面也有多部图的有效应用[1-7].

假设有n种不同的劳动工具用集合{l1,l2,…,ln}表示，而每名工作人员会使用一种或几种劳动工具去从事不同的工作，如何达到尽可能多的工作人员使用不同的劳动工具去从事不同的劳动，对于这类问题的解决，需要考虑的因素有人员、工具和工作.事实上，这是一类匹配的问题，但是如果采用2部图的模型已经不能解决该问题，因此必须建立新的数学模型，如3部图等.解决这类问题，一般地，若要考虑的因素有k个，那么可用k部图建立其相应的数学模型.

基于这类实际问题以及多部图的研究现状，本文提出关于多部图的最大匹配算法，不仅为研究多部图的匹配问题奠定了理论基础，而且对于图论本身也是一个贡献.

1 预备知识

文中关于图论的基本知识均来自文献[8-10]，下面仅复习其中几个概念.

(2) 设v∈V(G)，G中与顶点v关联的边的数目称为v在G中的度，记作deg(v).为方便起见，称度为零的顶点为孤立点.

(3) 图G称为k部图，若图G的顶点集V(G)被分成k个不相交的子集X1,X2,…,Xk，并且图G中没有任何一条边的2个端点在同一个Xj(j=1,2,…,k)中.

为表述方便，给一个新的概念.

定义2设G为一个k部图，V(G)=X1∪X2∪…∪Xk，其中Xi∩Xj=∅,(i≠j;i,j=1,2,…，k)，设M={v1v2,v2v3,…,vk-2vk-1,vk-1vk}为G的一个匹配.若M满足vj∈Xj(j=1,2,…,k)，则称M为G的一个通匹配.

2 模型建立

下面用一个3部图描述所研究的模型.在实际生活中，人们通过劳动得到应有的报酬，这样就有了人、劳动和报酬之间的关系，而不是人和报酬之间的直接关系.

设用u1,u2,…,us表示s个工作人员，t项工作用v1,v2,…,vt表示，用w1,w2,…,wm表示m种报酬，令X1={u1,u2,…,us}，X2={v1,v2,…,vt}，X3={w1,w2,…,wm}，V=X1∪X2∪X3,易知X1∪X2∪X3=∅.下面建立X1,X2,X3之间的关联边，若ui能胜任工作vj，则uivj之间有一条边相连接，i∈(1,2,…,s)，j∈{1,2,…,t}，若工作vj可以获得报酬wl，则vjwl之间有一条边相连，j∈{1,2,…,t}，l∈{1,2,…,m}，用E表示上面给出的所有边的集合，则得到一个3部图(X1,X2,X3;E)，如何安排工作可以使更多的工作人员得到报酬，这样问题可以转化为求3部图(X1,X2,X3;E)的最大通匹配问题.

故依据这类事实和图论基本知识，本文将解决多部图的有关内容，所研究的多部图的模型也是如上面的描述.

若图中存在孤立点，则占用空间大，增大了算法的复杂度，但孤立点的存在并不影响通匹配的结果，故本文对存在孤立点的图转化为无孤立点的图来研究.

3 算法

本节将给出多部图的数学模型的解决算法，并对该算法的复杂度给予分析.

3.1算法的伪码

Begin

M=∅；G=(X1,X2,…,Xk;E)；

|X1|=m；

for (i=1;i≤m;i++)

{

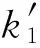
for (j=1;jlt;k;j++)

}

}

OutputM.

3.2算法的依据法则

算法是优先选取顶点度较小的元素，原因是若与该顶点匹配的元素较少，则应优先满足，不然很可能得不到最大匹配结果；为了排除已匹配过的顶点，下一步只对删去已匹配过顶点的剩余k部图进行匹配，这种匹配顶点排除法可以保证在进行下一步分析匹配状态时，不与已匹配过的顶点相重复.在上述算法中，由于max{|X1|,|X2|,…，|Xk|}lt;，必有算法过程存在某一顶点集为空集∅，这样算法在有限步内必停止，这时得到的匹配为最大通匹配.

3.3算法复杂度分析

令n=max{|X1|,|X2|,…,|Xk|}，由3.1给出的算法过程可以得到，求一个通匹配的算法复杂度为O(n(k-1))，而由于整个模型的最大匹配的个数至多为n，故整个算法的复杂度为O(n2(k-1)).

4 实例

下面通过一个实例说明，如何利用第3节给出的算法，得到相应的最大匹配问题.

某公司小组现有4名工人a11,a12,a13,a14，不同的时间段b21,b22,b23，有不同的操作车间c31,c32,c33,c34,c35，有不同的生产设备d41,d42,d43,d44，生产的产品为e51,e52,e53,e54，若工人a11可以工作的时间段为b21,b22，在时间段b21里可以在车间c31,c32里工作，使用的生产设备都为d41，设备d41可以生产的产品为e51,e52,e53，有关系的顶点之间有一条边相连.整个工作分配状态见图1，在这种状态下，寻求一个最佳方案，使尽可能多的工人参加生产产品的工作.

图1 5部图Fig.1 5-partite graph

由图1可以看出，这个问题可归结为一个讨论5部图的情况，此问题可以归结为第2节所建立的模型，故可由第3节给出的算法进行讨论.

Step15部图G=(X1,X2,X3,X4,X5;E)，X1={a11,a12,a13,a14}，X2={b21,b22,b23}，X3={c31,c32,c33,c34,c35}，X4={d41,d42,d43,d44}，X5={e51,e52,e53,e54}，匹配M=∅.

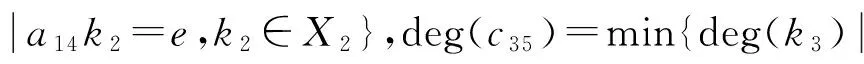
重复Step 2，得到的匹配M=M+a13b22c33d43e53+a12b21c31d41e51，此时K2=∅，算法停止.

这样，最大匹配结果为M={a14b23c35d44e54,a13b22c33d43e53,a12b21c31d41e51}.

求匹配a14b23c35d44e54的复杂度为O(9)，匹配a13b22c33d43e53的复杂度为O(10)，求匹配a12b21c31d41e51的复杂度为O(8)，求M的整个算法复杂度为O(27)与3.1节的算法复杂度一致，故3.1节的算法有效.

5 结束语

多部图的匹配在实际生活中有重要的应用，也是图论的重要组成部分.本文利用多部图的有关知识，为多部图的匹配问题提出新的算法，丰富了匹配的理论内容，此算法可以在做最大匹配时达到简单、快速之目的.在以后的工作中，我们继续研究有向图的匹配、加权图的匹配、有向加权图的匹配和最大流相关的各类问题，这些内容预计都可以借用这里的思想完成.

[1] 毛华，史田敏，李斌.补图方法在二部图最大匹配中的应用[J].黑龙江大学学报:自然科学版，2012,29(3):289-293.

[2] 胡先富，李娜. 格上传递矩阵的性质[J]. 四川师范大学学报:自然科学版，2009,32(6)：751-756.

[3] 于晶贤,宋岱才,赵晓颖,等.交巡警服务平台的合理调度研究[J].科学技术与工程学报，2012,12(1):126-128.

[4] 王伟，王锦彪. 中国民航飞机排班问题的多部图模型[J].交通与计算机学报，2008,26(4):112-115.

[5] Song Xiaoxin，Liang Hongwei.Cover the vertices of a tree by machings[J]. 郑州大学学报:理学版，2006,38(1):24-27.

[6] 孙波，钟声. 带匹配限制的交错路调课模型[J].广西师范大学学报:自然科学版，2007,25(4):100-103.

[7] 林翠琴. 图的匹配设计的矩阵构造法[J].系统科学与数学学报，2000,20(2):140-148.

[8] Bondy J A, Murty U S R. Graph Theory with Applications[M]. New York: Elsevier, 1976:70-90.

[9] Bondy J A, Murty U S R. Graph Theory[M]. Berlin: Springer, 2008:67-120.

[10] Tutte W T. Graph Theory[M].Cambridge: Cambridge University Press, 2001:16-40.

AnAlgorithmonMaximumMatchingofMultipartiteGraph

MAO Hua, ZHAO Xiao-na, SHI Tian-min, MAO Xiao-liang, LIU Hui

(CollegeofMathematicsandComputerScience,HebeiUniversity,Baoding071002,China)

As an important branch in graph theory, matching theory was applied in many fields such as combinatorial optimization, linear programming, artificial intelligence theoretical and matrix theory. An algorithm was provided relative to solving with the maximum matching of multipartite graph. The practicability and effectiveness of this algorithm was illustrated by a simulation example. This algorithm explored a new way dealing with complex allocation problems.

matching theory; maximum matching; multipartite graph

2012-10-30

保定市科学技术研究项目,编号11ZG005.

毛华(1963- )，女，教授，博士，主要从事概念格、数据挖掘、组合数学及网络物流方向研究，E-mail:mh@hbu.edu.cn；通讯作者：赵小娜(1985-)，女，硕士，主要从事图论和网络物流研究，E-mail:shitianminzi@126.com.

O 23

A

1671-6841(2013)01-0027-03

10.3969/j.issn/1671-6841.2013.01.007