非线性扩散方程的条件Lie-Bäcklund对称和符号不变量

姬利娜， 郑群珍

(1.河南农业大学 信息与计算科学系 河南 郑州 450002； 2.河南教育学院 数学系 河南 郑州 450046)

非线性扩散方程的条件Lie-Bäcklund对称和符号不变量

姬利娜1， 郑群珍2

(1.河南农业大学 信息与计算科学系 河南 郑州 450002； 2.河南教育学院 数学系 河南 郑州 450046)

考虑了径向对称非线性扩散方程的条件Lie-Bäcklund对称和符号不变量.允许二阶条件Lie-Bäcklund对称和一阶Hamilton-Jacobi型符号不变量的方程被确定给出,并由对称约化得到了方程的不变解.

非线性扩散方程； 条件Lie-Bäcklund对称； 符号不变量

0 引言

文献[1-2]分别独立地引入了条件Lie-Bäcklund对称方法.如同Lie-Bäcklund对称方法是对古典对称方法的推广一样，条件Lie-Bäcklund对称方法是对非古典对称方法的自然推广.计算条件Lie-Bäcklund对称的过程和计算非古典对称的一样，最重要的是事先给定条件Lie-Bäcklund对称的形式.

事实证明条件Lie-Bäcklund对称方法是对非线性扩散方程进行对称约化的有效方法之一[3-4]，还可给出分离变量[5]和不变子空间[6]的对称群解释.该方法和 Hamilton-Jacobi型符号不变量也是密切相关的[7-8].对二阶的非线性扩散方程，关于其二阶条件Lie-Bäcklund对称的结果可转化为其Hamilton-Jacobi 型符号不变量.符号不变量的思想源于氧化反应扩散方程的爆破奇性分析.Hamilton-Jacobi 型符号不变量可对非线性抛物型方程的通解进行确界估计，该量也可用于研究通解的渐近行为和性态.

本文考虑径向对称的非线性扩散方程

(1)

的二阶条件Lie-Bäcklund对称和一阶Hamilton-Jacobi型符号不变量及其不变解，其中D(u)=uk,Q(r,u)分别为扩散项和源项.该方程可用于描述非线性热扩散以及非牛顿流体的非线性剪流等[9-10].

1 基本定理和记号

下面给出非线性演化方程的条件Lie-Bäcklund对称方法和符号不变量方法的基本定义和命题.令

(2)

是具特征η的演化向量场，且

ut=E(r,t,u,u1,…,un)

(3)

是一非线性演化方程，其中，

定义1演化向量场 (2) 称作方程 (3) 的Lie-Bäcklund对称当且仅当

V(ut-E)|L=0,

定义2演化向量场 (2) 称作方程 (3) 的条件Lie-Bäcklund对称当且仅当

V(ut-E)|L∩M=0,

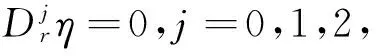
下面的命题在计算条件Lie-Bäcklund对称时是至关重要的.

命题1[1-2]方程 (3) 允许条件Lie-Bäcklund对称 (2) 的充分条件是存在W(t,r,u,η)使得

(4)

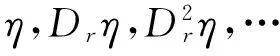
该命题的明显推论是，若

Dtη|L∩M=0,

(5)

则方程(3)允许具特征η的条件Lie-Bäcklund对称.

令

J(r,u)=J(r,t,u,ut,ur)

(6)

是一阶Hamilton-Jacobi算子，其中J(·)是充分光滑的.

定义3[11]算子(6)是方程(3)的Hamilton-Jacobi型符号不变量，等价于算子 (6) 在方程(3)的解流行上具有保号性，即

J(r,u)≥0(≤0),t=0,
⟹J(r,u)≥0(≤0),tgt;0.

对方程 (1)，我们考虑具特征

(7)

的条件Lie-Bäcklund对称.不难证明算子

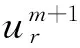
(8)

是方程(1)的Hamilton-Jacobi型符号不变量.证明过程如文献[7]中的命题 2.1.

2 方程(1)的条件Lie-Bäcklund对称和符号不变量

由(5)直接运算可得关于ur的多项式恒为0，故该多项式的系数为0.即方程 (1) 允许条件Lie-Bäcklund对称(7)的充分条件是H(u),G(r,u),F(r,u),Q(r,u)和满足非线性偏微分方程组，即所谓的决定方程组.值得注意的是对于特殊的m=2,-1,-2，多项式的某些项可以合并.因而这些特殊情形会引入新的决定方程组.求解这些决定方程组可以得到新的结果.由(8)可确定方程(1)允许的Hamilton-Jacobi型符号不变量(8).由方程(1)和其允许的条件Lie-Bäcklund对称的相容性可对方程进行对称约化得到其不变解.先由η=0得到含有依赖于t的积分常数的解，将其代入原方程可确定与t相关的积分常数.下面给出几个例子表明该约化过程.

例1方程

(9)

允许条件Lie-Bäcklund对称

和Hamilton-Jacobi型符号不变量

方程 (9) 的解为

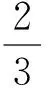
其中α(t)和β(t)满足

α′+(n-3)β2-b=0, 2β′-3β3+3a=0.

例2方程

(10)

允许条件Lie-Bäcklund对称

和Hamilton-Jacobi型符号不变量

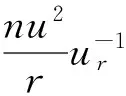
方程 (10) 的解如下给出:

当a≠0时,

其中α(t)和β(t)满足

当a=0时,

u(r,t)=rα(t)β(t),

其中α(t)和β(t)满足

α′=b,β′=nα-1β+c+d+1.

例3方程

(11)

允许条件Lie-Bäcklund对称

和Hamilton-Jacobi型符号不变量

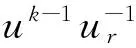
方程 (11) 的解如下给出:

当k≠3时,

其中α(t)和β(t)满足

当k=3时,

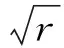
其中α(t)和β(t)满足

α′=2α-1+b;β′=4nα-2+a+c.

3 结论

本文给出了方程(1)的二阶条件Lie-Bäcklund对称和一阶Hamilton-Jacobi型符号不变量的结构.允许条件Lie-Bäcklund对称(7)和符号不变量(8)的非线性扩散方程被确定给出.通过对称约化得到了方程相应的不变解.对非线性扩散方程，二阶条件Lie-Bäcklund对称约化是行之有效的,可以得到许多有意思的结果.在以后的工作中，我们可考虑其他类型的条件Lie-Bäcklund对称，如高阶的条件Lie-Bäcklund对称，可能得到其他有意思的结果.

[1] Zhdanov R Z. Conditional Lie-Bäcklund symmetry and reduction of evolution equation[J]. J Phys A: Math Gen, 1995, 28 (13): 3841-3850.

[2] Fokas A S, Liu Qingming. Nonlinear interaction of traveling waves of nonintegrable equations[J]. Phys Rev Lett, 1994, 72 (21): 3293-3296.

[3] Qu Changzheng. Group classification and generalized conditional symmetry reduction of the nonlinear diffusion-convection equation with a nonlinear source[J]. Stud Appl Math, 1997, 99(2): 107-136.

[4] Ji Lina, Qu Changzheng. Conditional Lie-Bäcklund symmetries and solutions to (n+1)-dimensional nonlinear diffusion equations[J]. J Math Phys, 2007, 48(10): 103509.

[5] Qu Changzheng, Zhang Shunli, Liu Ruochen. Separation of variables and exact solutions to quasilinear diffusion equations with nonlinear source[J]. Physica D, 2000, 144(1): 97-123.

[6] Ji Lina, Qu Changzheng. Conditional Lie-Backlund symmetries and invariant subspace to nonlinear diffusion equations[J]. IMA J Appl Math, 2011, 76(4): 610-632.

[7] Qu Changzheng, Estevez P G. On nonlinear diffusion equations withx-dependent convection and absorption[J]. Nonlin Anal TMA, 2004, 57(4): 549-557.

[8] Ji Lina, Qu Changzheng, Wang Lizhen. Conditional Lie-Bäcklund symmetries and sign-invariants to quasilinear diffusion[J]. Stud Appl Math, 2007, 119(4):355-391.

[9] Pascal J P, Pascal H. On some diffusive waves in nonlinear heat conduction[J]. Int J Nonlin Mech, 1993, 28(6): 641-649.

[10] Pascal J P, Pascal H. On some nonlinear shear flows of non-newtonian fulids[J]. Int J Nonlin Mech, 1995, 30(4): 487-500.

[11] Galaktionov V A. Quasilinear heat equations with first-order sign-invariants and new explicit solutions[J]. Nonlin Anal TMA, 1994, 23(12): 1595-1621.

Sign-invariantsandConditionalLie-BäcklundSymmetriesoftheNonlinearDiffusionEquations

JI Li-na1, ZHENG Qun-zhen2

(1.DepartmentofInformationandComputationalScience,HenanAgriculturalUniversity,Zhengzhou450002,China; 2.DepartmentofMathematics,HenanInstituteofEducation,Zhengzhou450046,China)

The conditional Lie-Bäcklund symmetries and sign-invariants of the radially symmetric non-linear diffusion equations were considered. The equations, which admitted of second-order conditional Lie-Bäcklund symmetries and first-order Hamilton-Jacobi sign-invariants, were obatined and the corresponding invariant solutions to the resulting equations were also obtained due to symmetry reductions.

nonlinear diffusion equations; conditional Lie-Bäcklund symmetry; sign-invariants

2012-11-08

国家自然科学基金资助项目，编号U1204104.

姬利娜(1979-)，女，讲师，博士，主要从事微分方程研究, E-mail:jilina@henau.edu.cn.

O 175.14

A

1671-6841(2013)01-0001-04

10.3969/j.issn/1671-6841.2013.01.001