舰载直升机旋翼/机体耦合动力学稳定性
2013-03-19向锦武
刘 洋 向锦武
(北京航空航天大学 航空科学与工程学院,北京 100191)
直升机以其特有的垂直起降和低空低速飞行特点,越来越多的装备于海上舰船用于反潜、反舰、中继制导和海上补给、救援等任务.海面不仅风速大而且甲板建筑对风场有很强的干扰,再加上舰船在海面恶劣环境下的大幅震荡,舰载直升机起飞和着陆条件受到严格限制.
舰载直升机不同于路基直升机,必须要适应复杂的工作环境.其在甲板上的动力学响应和稳定性问题与路基直升机相比有很大不同.舰载直升机在舰面工作时,如果旋翼与机体振动频率耦合就可能发生“舰面共振”事故,使机体和旋翼振幅过大,对机上设备和人员造成损害.“舰面共振”是舰载直升机起飞和着舰过程中发生的严重事故的一种,并且发生概率较大[1].与路基直升机建模方法不同,舰载直升机动力学建模时,需要考虑舰船运动对系统的影响.文献[2]考虑舰船滚转运动和海面阵风的影响建立舰载直升机的动力学模型.文献[3]用有限元模拟旋翼桨叶并且计入舰船6个运动自由度建立了直升机和舰船耦合的动力学模型.文献[4]考虑直升机在甲板上的不同位置及舰面流场等因素,建立了舰船甲板上直升机旋翼/机体耦合动力学分析模型.文献[5]建立了较详细的起落架模型分析机体在甲板上的操纵动力学问题.文献[6]用复刚度的方法得到在非对称载荷和非对称变形情况下研究轮式起落架“舰面共振”的方法.
直升机在舰面起降时,舰船摇晃运动作用在机身上的惯性载荷加上甲板平面的倾斜,使直升机起落架产生非对称变形和非对称载荷.由于起落架具有非线性特性,起落架系统结构参数在海面情况下与路面情况相比有较大不同.虽然上面学者的研究都在直升机动力学模型上考虑了舰船运动的影响,但是忽略了起落架的非线性特性对旋翼/机体耦合稳定性的影响.
本文结合舰载直升机的起落架非对称和非线性特点,采用无轴承旋翼直升机为平台,考虑舰船的横摇和纵摇两个方向自由度,建立了舰载直升机旋翼机体耦合动力学分析模型.将起落架分为油压作动器和橡胶轮胎两部分,分别考虑二者的非线性特点,并且根据直升机在舰船的平衡情况得到起落架系统的非对称特性.通过计算分析了甲板倾斜和鱼叉系留装置对舰载直升机“舰面共振”的影响.
1 动力学模型
舰载直升机在舰面起降时,舰船在海面的振动会通过起落架传递给机体,同时机体和旋翼系统在起落架上也会发生振动.但是机体与旋翼的振动频率相比舰船的振动频率要高很多(两者相差20倍以上),可以将舰船振动作用在直升机上的惯性载荷设定为不变载荷,并且在直升机动力学建模时可以假定甲板平面始终保持某一角度固定不变[6].在分析模型中,认为舰船是刚性的,具有2个刚体转动自由度(横滚、俯仰).这里忽略了舰船的沉浮自由度,是因为舰载直升机起落架产生非对称特性变化的原因主要与舰船的横滚和俯仰自由度有关.直升机机体假设为刚体,有5个运动自由度,其中有3个平动自由度(航向、侧向、纵向)和2个转动自由度(横滚、俯仰).舰船和机体的坐标如图1所示.

图1 舰载直升机分析模型
1.1 旋翼动力学模型
根据哈密顿原理直升机的动力学方程为
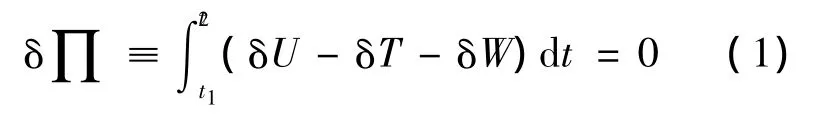
式中,δU为应变能变分;δT为动能变分;δW为外力虚功.应变能、动能和外力虚功分为机身和旋翼部分,如式(2)~式(4)所示,旋翼由Nb片桨叶构成.
无轴承旋翼模型包括主桨叶、柔性梁、扭矩套、摆振销和变距拉杆(图2).由于无轴承旋翼桨叶根部变形较大并且具有多路传力的特点,采用中等变形梁理论把主桨叶、柔性梁和扭矩套离散成15个结点的梁单元[7],并且在桨叶根部考虑摆振销和线性刚度变距拉杆的约束.
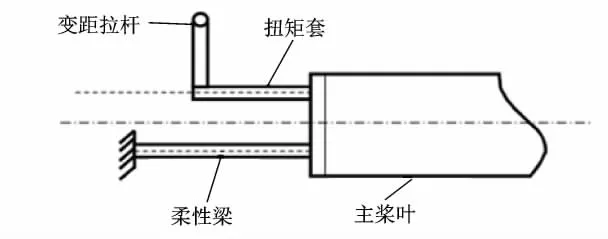
图2 无轴承桨叶模型
桨叶的应变能计算采用Green应变计入非线性的应变位移关系.由中等变形梁理论[8]推导出桨叶的应变能变分为

旋翼系统的动能通过桨叶上任意一点在惯性坐标系下的速度Vp积分得到.单片桨叶的动能表达式为
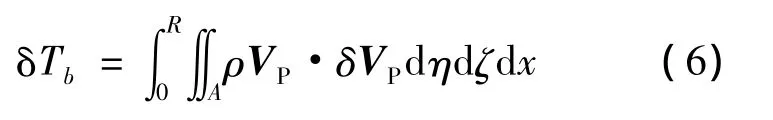
桨叶剖面气动模型采用准定常理论,旋翼入流模型采用文献[9]动力入流模型.通过桨叶剖面速度得到桨叶剖面的环量气动力和非环量气动力,沿桨叶半径积分可得到整个桨叶的气动力虚功表达式为
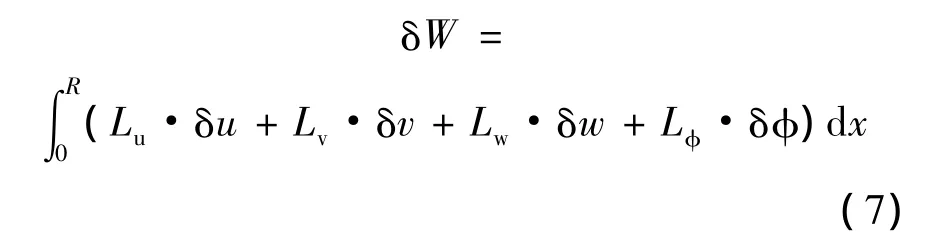
1.2 起落架模型
不同于路基直升机,舰载直升机在舰船上不能始终保持水平起降.舰船运动作用于机体的惯性载荷与机体倾斜引起机体重力分力使得左右主起落架产生非对称载荷和非对称变形(图3).考虑到起落架的非线性和非对称特性,舰载直升机的起落架参数与路基直升机有较大不同,因此旋翼机体耦合稳定性也发生较大变化.本文起落架为三点式轮式起落架,假设左右主起落架轮胎均处于刹车状态,并且轮胎始终与地面保持接触,并且不发生滑动摩擦.鱼叉装置假设为机体底部的一组约束力作用于机体.针对舰载直升机起落架在舰面非对称特点,首先根据舰船运动情况对直升机系统进行配平计算,然后通过对起落架受力计算得到起落架的非对称刚度和阻尼,最后在此系统参数下判断直升机旋翼机体系统的阻尼和频率便可得到非对称和非线性起落架系统对舰载直升机“舰面共振”稳定性的影响.
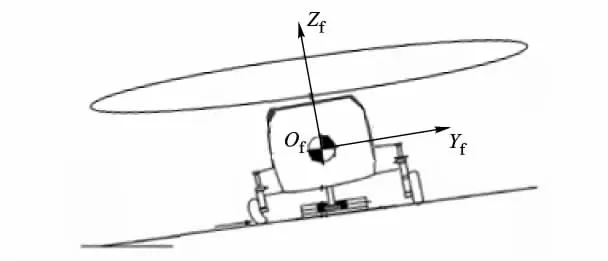
图3 直升机在倾斜甲板上平衡位置示意图
直升机轮式起落架由油压作动器(缓冲支柱)和橡胶轮胎构成[10](图4),起落架上受到载荷与机身轴Zf平行.根据文献[10],发生变形后缓冲支柱受到载荷为
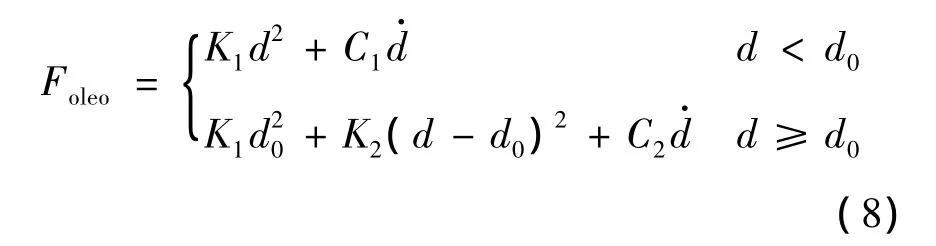
式中,d为缓冲支柱变形量;d0由缓冲支柱结构参数确定液压作动器所受载荷,为二阶分段非线性(图5).随载荷增加,起落架的刚度和阻尼也会发生变化.

图4 起落架结构模型
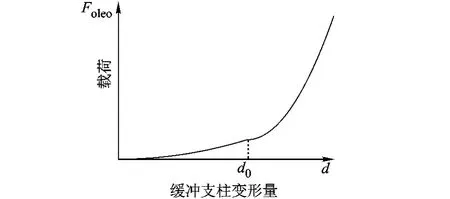
图5 起落架载荷随位移的变化
考虑橡胶轮胎模型在Zf方向具有线性的刚度和阻尼,轮胎的垂向载荷为
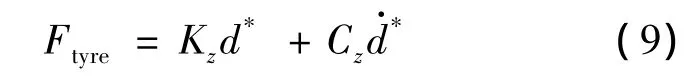
式中,d*为轮胎的垂向变形量.由于忽略了液压作动器和轮胎的质量,轮胎受到的垂向载荷等于缓冲支柱的垂向载荷,即

起落架轮胎受压后(图6),在XsOYs平面内产生平行于舰船甲板平面的静摩擦力.
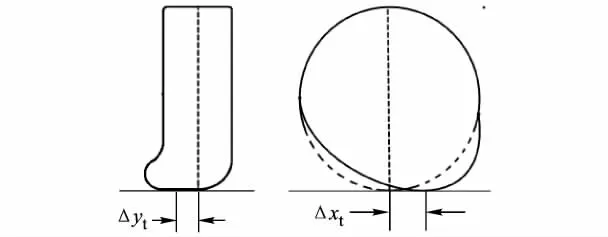
图6 轮胎在甲板平面内的变形
此时轮胎模型简化为三维的弹簧阻尼系统,根据文献[10],轮胎变形后在甲板平面(XsOYs平面)内的弹性系数为

式中C1,C2,C3由轮胎的结构参数确定.轮胎在甲板平面内的弹性恢复力为

式中Δxt和Δyt为轮胎在甲板平面内的变形量.
2 模型验证
通过对系统配平计算,得到桨叶和起落架在甲板上的平衡位置.在平衡位置处计算起落架参数,并对系统做小扰动假设得到系统的扰动方程.对扰动方程做多桨叶坐标变换,将桨叶的运动方程从旋转坐标系转换到固定坐标系下,可以得到固定坐标系下的舰载直升机旋翼/机体的耦合动力学方程.将系统方程组转换成一阶微分方程组的形式,计算方程组的特征根,其复特征值实部即为系统的阻尼,虚部为系统频率.通过判断系统的频率和阻尼,就可以对旋翼/机身耦合的稳定性做出分析.
为了验证模型的正确性,对无轴承旋翼直升机“地面共振”稳定性问题做了算例验证.直升机系统主要参数见表1,详细参数见文献[7].
桨叶模型离散成6个梁单元,分别为两个柔性梁单元、两个扭矩套单元和两个桨叶单元.通过计算得到直升机旋翼和机体耦合系统的频率随旋翼转速变化图(图7a),和最不稳定的模态——旋翼摆振后退振型模态阻尼随转速变化图(图7b),其中实验数据为参考文献[7]中数据.

图7 无轴承旋翼与机体系统的频率和阻尼
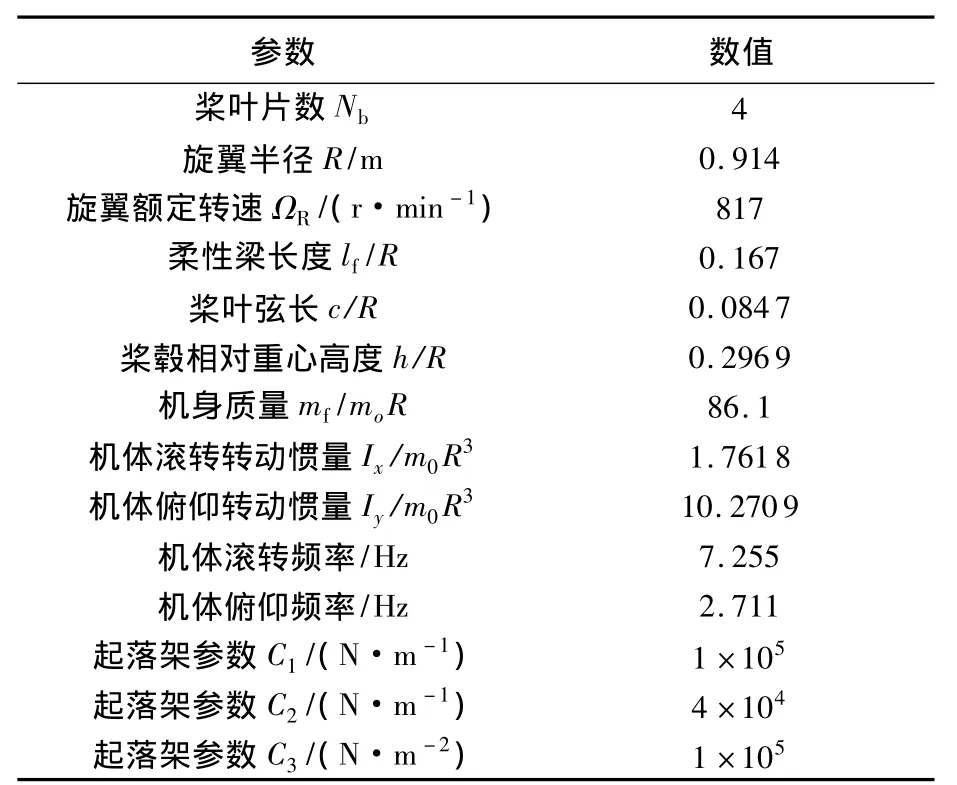
表1 直升机系统参数
从结果可以看出,分析模型对无轴承旋翼直升机“地面共振”计算值与实验值较吻合.
3 舰面共振计算
3.1 舰面倾斜对稳定性影响
舰载直升机在甲板上起降时,旋翼与机体会随着舰船在海面发生震荡,起落架平面与水平面的夹角会随着舰船的摇摆发生变化.由于起落架的非线性特性,舰载直升机的结构参数与地面情况相比具有不同的刚度和阻尼,其旋翼机体耦合系统的稳定性也发生变化,使舰载直升机很有可能发生“舰面共振”事故.为了重点分析甲板倾斜对直升机“舰面共振”的影响,本文考虑舰船在海面只有横摇运动,针对舰船10°振幅的横摇振动,计算了“舰面共振”的频率和摆振后退阻尼随转速变化图(图8).从结果看出在甲板具有10°倾斜角时,由于起落架的非对称和非线性特性,直升机机体的滚转刚度和阻尼都发生变化.由于机体的滚转刚度变小,其与旋翼摆振后退振型发生共振的频率提前出现,使得不稳定转速范围提前出现,很容易导致“舰面共振”事故发生.
3.2 鱼叉系留影响
为了增加舰载直升机系统在舰面的安全性,一般在机体底部装有鱼叉等系留装置,鱼叉系留装置增加了机体在舰面的约束.系统附加多余约束力使起落架变形量增加,从而增加了机体的刚度和阻尼,旋翼机体系统的动力学特性也会变化.仍然考虑舰船只有横摇振动的情况,在横摇振幅为10°时,计算了鱼叉装置系留情况下旋翼机体系统的频率和阻尼(图9).从结果看出鱼叉装置增加了机体的滚转刚度和俯仰刚度,并且提高了系统阻尼.鱼叉系统的约束力作用在机体底部,使得液压作动器和轮胎垂向压缩量增加,通过对此平衡位置系统参数计算,发现由于起落架系统具有非线性特性,鱼叉系留提高了机体模态的刚度,从而推迟了不稳定旋翼转速区域,大大超出了额定工作转速范围发生,可以很好地遏制直升机“舰面共振”事故发生.
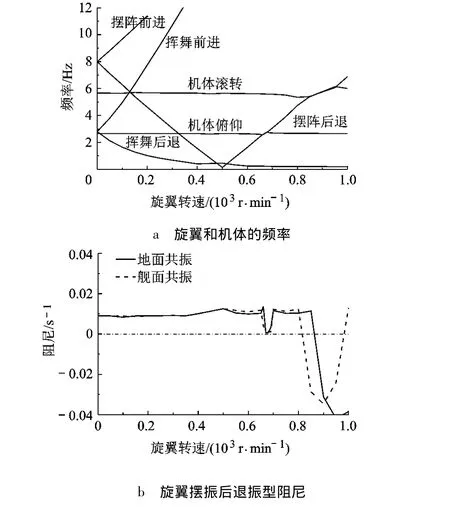
图8 舰面情况下系统的频率和阻尼
4 结 束 语
本文建立了舰载直升机的动力学分析模型,模型考虑了甲板平面倾斜和鱼叉系留情况下轮式起落架的参数变化.该模型结合无轴承旋翼直升机桨叶大变形和桨叶根部多路传力的特点,可以较准确地分析无轴承旋翼直升机的“地面共振”和“舰面共振”稳定性问题.结合舰载直升机轮式起落架的非线性和非对称特点,分析了直升机“舰面共振”发生和预防的机理.甲板平面的倾斜会使系统的刚度和阻尼降低,发生“舰面共振”不稳定转速区域提前出现.但是在系留装置作用下,系统的刚度和阻尼增加并且延缓了“舰面共振”不稳定转速区域的出现.
References)
[1]马强,朱旭程.舰载直升机起飞着舰事故模式影响及危害性分析[J].海军航空工程学院学报,2012,27(2):209 -214 Ma Qiang,Zhu Xucheng.Failure mode effect and criticality analysis of shipboard helicopter during launch and recovery[J].Journal of Naval Aeronautical Engineering Institute,2012,27(2):209-214(in Chinese)
[2] William P,Geyer J.Aeroelastic analysis of transient blade dynamics during shipboard engage/disengage operations[J].Journal of Aircraft,1998,35(3):445 -453
[3] Han Dong,Wang Haowen,Gao Zheng.Aeroelastic analysis of a shipboard helicopter rotor with ship motions during engagement and disengagement operations[J].Aerospace Science and Technology,2012,16(1):1 -9
[4]胡国才,孙建国,刘湘一.直升机舰面动力学分析模型[J].海军航空工程学院学报,2008,23(5):481-485 Hu Guocai,Sun Jianguo,Liu Xiangyi.Analytical model of helicopter on-deck dynamic interface[J].Journal of Naval Aeronautical Engineering Institute,2008,23(5):481 -485(in Chinese)
[5] Darren R L,Robert G L.Development and experimental validation of a shipboard helicopter on-deck maneuvering simulation[J].Journal of Aircraft,2006,43(4):895 - 906
[6]徐敏.一种分析轮式起落架直升机“舰面共振”的方法[J].航空学报,2007,28(4):886 -890 Xu Min.Analytical method of ship resonance for helicopter with wheel landing gears[J].Acta Aeronautica et Astronautica Sinica,2007,28(04),886 -890(in Chinese)
[7] Jinseok Jang.Ground and air resonance of bearingless rotors in hover and forward flight[D].Maryland:Department of Aerospace Engineering,University of Maryland,1988
[8] Hodges D H,Dowell E H.Nonlinear equations of motion for the elastic bending and torsing of twisted nonuniform rotor blades[R].NASA TN D-7818,1974
[9] Gaonkar GH,Peters D A.Review of dynamic inflow modeling for rotorcraft flight dynamics[J].Vertica,1998,12(3):213 -242
[10] Blackwell J,Feik R A.A mathematical model of the on-deck helicopter/ship dynamic interface[R].ARL Aero TM405,1988
