遥控模式下无人机系统纵向飞行品质评定
2013-03-19黄成涛王立新
黄成涛 王立新
(北京航空航天大学 航空科学与工程学院,北京 100191)
无人机的飞行事故率较高,为有人机的10~100倍[1],尤其是在遥控着陆阶段.要保证无人机的飞行安全与完成飞行任务的质量,无人机系统(由无人机平台、通信数据链和地面控制站等模块组成)须具有较好的飞行品质.
遥控模式下,无人机系统的飞行品质存在以下特点:①通信数据链时延对系统闭环飞行品质的影响较大[2-3];②目前,国内外尚无专门针对无人机系统的飞行品质标准,只能根据其特点,参照部分有人机的飞行品质准则[4];③地面无人机飞行员无法直接感受到无人机的过载等状态信息,基于无人机飞行员感受这些状态信息的飞行品质准则应谨慎使用[4].
目前,国内外已在无人机本体的飞行品质评定[5-6]、无人机飞行品质标准制定[1,4,7]等方面开展了研究.但是,针对无人机系统开展飞行品质评定方法研究,评定并分析无人机系统的飞行品质特性,则较少见诸报道.
针对上述问题,本文基于有人机的飞行品质准则和评定方法,较系统地研究了遥控模式下无人机系统的纵向飞行品质评定方法.对算例无人机系统的纵向短周期飞行品质及驾驶员诱发振荡(PIO,Pilot-induced Oscillations)趋势进行了评定,得出了无人机系统纵向飞行品质的新特点.
1 无人机系统模型
无人机系统包括地面控制站、通信数据链和无人机平台等模块,如图1所示.

图1 无人机系统模型结构
地面控制站接收无人机飞行员的操纵指令,并向地面飞行员提供无人机的飞行状态等信息.
通信数据链分为上行和下行链路.在评定遥控模式下无人机系统的飞行品质时,操纵信号应取为无人机飞行员的操纵输入,而飞行状态信息应从地面控制站获取.通信数据链时延应取为上行和下行链路的时延之和.
无人机平台由飞控系统、执行器和无人机本体等构成.机载飞控系统基于PI控制增稳方法设计,可较好地控制无人机跟踪输入指令.
执行器包括发动机和舵面,均选取一阶惯性环节来描述其动力学特性,并考虑舵面最大偏角和偏转速率以及发动机推力范围的限制.
选取某无人机为研究对象,计算所需数据来源于包括风洞试验在内的各种试验和理论计算.
2 评定方法
飞控系统抑制了长周期模态运动,本文只研究无人机系统的短周期飞行品质及PIO趋势.
2.1 短周期飞行品质评定方法
评定飞机短周期飞行品质的准则包括CAP准则、等效参数准则、带宽准则和Neal-Smith准则等[8].有人建议在能够获得准确飞行品质的前提下,尽量简化或减少使用这些准则[9].
1)CAP准则
该准则基于飞机的短周期自然频率ωsp、阻尼比ξsp、单位迎角增量的稳态过载增量Δnz/Δα、操纵期望参数CAP和等效延迟时间τe来评定飞机的短周期飞行品质.其中,CAP可反映轨迹与姿态的协调性,并可反映飞机的操纵性[9].
本文建议在无人机系统的设计过程中采用CAP准则来预测其短周期飞行品质,以全面考察系统的短周期频率、阻尼、等效延迟时间、轨迹与姿态的协调性和操纵性等特性.
根据无人机系统(图1)在给定激励信号下的飞行仿真结果,利用低阶等效系统方法[9],可得到 ωsp、ξsp、Δnz/Δα、CAP 和 τe,进而可按照 CAP准则来评定其短周期飞行品质.
2)等效参数准则
等效参数准则所考察的飞机的短周期频率、阻尼、等效延迟时间等特性,CAP准则均可考察.在采用CAP准则后,可不采用等效参数准则.
3)Chalk准则
Chalk准则主要考察飞机的等效延迟时间和短周期阻尼等特性,而这些特性CAP准则均可考察.因此,在低阶等效系统失配度较小的情况下,采用CAP准则后,可不采用Chalk准则.
4)Gibson准则
Gibson准则只给出了一些趋向性的指导,未给出具体的品质等级边界,不建议采用该准则.
5)带宽准则
带宽准则主要考察飞机俯仰角θ频域响应的带宽ωBW和时间延迟τp.其中,ωBW表征θ对俯仰操纵的频域响应在保证6 dB及45°稳定裕度的前提下,人机闭环系统能够复现的俯仰角指令的最大频率,反映人机闭环系统响应的快速性.
本文建议采用带宽准则来评定遥控模式下无人机系统的飞行品质,以考察人机闭环响应的快速性和无人机系统的延迟时间.
通过对无人机系统在给定激励信号下的飞行仿真结果进行快速傅里叶变换[9],可得到θ对俯仰操纵输入的频域响应曲线,进而可得到ωBW和τp,然后可对系统的短周期飞行品质进行评定.
6)Neal-Smith准则
该准则能揭示出人机闭环θ响应在期望的闭环带宽ωB下,是否具有振荡或超调等倾向(与最大谐振|θ/θc|max有关),并可反映驾驶员的操纵负担(与驾驶员补偿相角φp有关).其中,ωB反映闭环响应的快速性,ωB越大,θ响应越快,为确保飞行任务的完成质量,ωB须符合准则的要求.
本文建议采用Neal-Smith准则来评定无人机系统的飞行品质,以考察人机闭环俯仰角响应的振荡或超调倾向,以及无人机飞行员的操纵负担.
无人机飞行员是根据通信数据链下传的无人机飞行状态信息来感受飞机的俯仰姿态响应,进而进行纵向操纵.因此,根据Neal-Smith准则,无人机飞行员模型如下式所示:

式中,e-0.25s表示无人机飞行员的时间滞后;Kpe,Tp1和Tp2分别表示无人机飞行员的增益、超前补偿时间常数和滞后补偿时间常数,其大小及相互关系反映无人机飞行员的工作负担.
通过对人机闭环系统在给定激励信号下的飞行仿真结果进行快速傅里叶转换[9],可得到θ频域响应曲线,据此可得 ωB,|θ/θc|max和闭环回落量Δ等.采用优化方法,以ωB与准则要求的闭环带宽(着陆阶段为2.5 rad/s)之差最小,且 Δ≥-3 dB为优化目标;以 Kpe,Tp1和 Tp2为自变量[10],可得到满足优化目标的 φp和|θ/θc|max,进而可根据该准则来评定无人机系统的短周期飞行品质.
综上,本文建议采用CAP准则、带宽准则和Neal-Smith准则来评定遥控模式下无人机系统的短周期飞行品质,如表1所示.

表1 遥控模式下无人机系统短周期飞行品质评定方法
2.2 PIO趋势预测方法
PIO分为3类,I类PIO是由于飞机系统相位滞后或时延过大而产生的线性人机耦合振荡.由于无人机系统的延迟时间较大,遥控模式下,发生I类PIO的趋势较高.
MIL-STD-1797A[8]推荐了一种准则来预测 I类PIO.该准则认为,驾驶员在进行俯仰跟踪时,当在准则频率ωR处发生弱阻尼振荡时,驾驶员会企图控制法向过载来消除误差.但是,无人机飞行员不能直接感受到无人机的过载,不会将过载作为直接控制目标.因此,本文不建议采用该准则来预测无人机的PIO趋势.
此外,预测飞机PIO的方法还有带宽准则和Neal-Smith 准则等[9].
1)带宽准则
该准则主要依据θ响应的带宽ωBW和时间延迟τp来预测飞机的PIO趋势.如果ωBW过小,人机闭环θ响应会较缓慢.在需要θ快速响应时,驾驶员所需的增益和超前补偿需增大,导致θ响应的超调和振荡增大,进而引起PIO现象.τp过大时,为确保θ快速响应,驾驶员所需增益和超前补偿亦需增大,亦会引起PIO现象.该准则预测飞机俯仰跟踪和着陆状态的PIO敏感性时效果较好,且还可评定无人机系统的短周期飞行品质.因此,建议采用该准则来预测无人机的PIO趋势.
2)Neal-Smith准则
该准则依据人机闭环系统在期望的闭环带宽ωB(反映闭环θ响应的快速性)下,θ响应的最大谐振|θ/θc|max和驾驶员补偿相角 φp来预测飞机的PIO倾向.为确保飞行任务的完成质量,ωB须满足该准则的要求,此时:①如果|θ/θc|max过大,人机闭环θ响应会具有较强烈的振荡和超调倾向,可能引起PIO现象;②如果φp过大,表明驾驶员需进行较大的超前补偿操纵,其操纵负担较大,如果驾驶员减小超前补偿时,则|θ/θc|max会增大,亦可能引起PIO现象.因此,该准则可较好地揭示出PIO倾向.此外,该准则还可评定无人机系统的短周期飞行品质.因此,建议采用该准则来预测遥控模式下无人机系统的PIO趋势.
综上,本文建议采用带宽准则和Neal-Smith准则来预测遥控模式下无人机系统的PIO趋势.
3 纵向飞行品质评定
选取算例无人机处于着陆阶段(C种阶段).为研究通信数据链时延τd不同时无人机系统的纵向飞行品质特性,本文选取τd分别为0(仅用于对比分析,τd并不会为0),0.1,0.2 和0.5 s.
3.1 CAP 准则评定
通过低阶等效系统方法,可得到算例无人机系统的CAP准则参数,结果如表2所示.
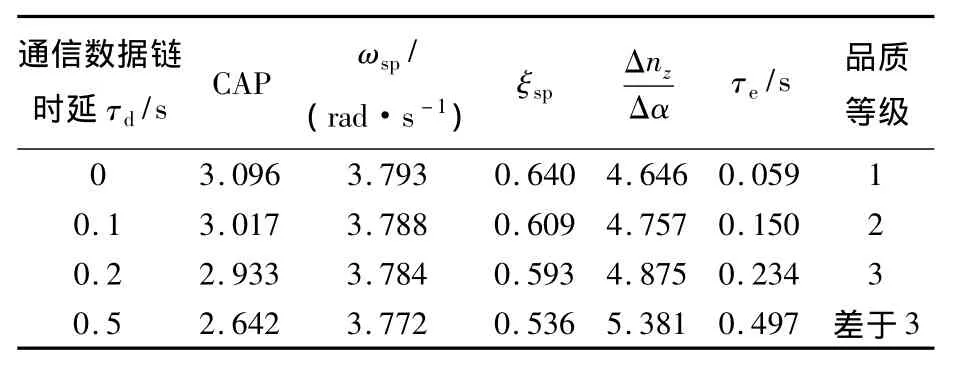
表2 CAP准则飞行品质评定结果(C种阶段)
由表2可看出,无人机系统的 ωsp,ξsp,CAP和Δnz/Δα均可满足1级飞行品质的要求,且这些参数受τd的影响较小.这是因为通过飞控系统的设计,无人机平台的 ωsp,ξsp,CAP 和 Δnz/Δα 均可得到较好改善,且这些参数主要取决于无人机平台.τd增大会使得无人机系统的等效延迟时间τe增大,会导致短周期飞行品质发生降级.
3.2 带宽准则评定
根据带宽准则对算例无人机系统的纵向飞行品质进行评定,结果如表3、图2和图3所示.图3中,tdb为姿态回落时间.

表3 带宽准则飞行品质评定结果(C种阶段)

图2 带宽准则短周期飞行品质评定结果(C种阶段)

图3 带宽准则PIO趋势预测结果(C种阶段)
由表3和图2可看出,通信数据链时延τd对无人机系统的带宽ωBW和时间延迟τp的影响均较大.τd增大会使τp增大,导致系统的短周期飞行品质发生降级.此外,τd增大还会导致ωBW减小,人机闭环响应的快速性下降,对系统的短周期飞行品质亦具有不利的影响.当τd较大时,无人机系统的短周期飞行品质会发生明显降级.
由表3和图3可看出,τd增大会导致τp增大和ωBW减小,使无人机的PIO趋势增大.τd较大时,遥控模式下的无人机会具有敏感的PIO趋势.
3.3 Neal-Smith 准则评定
根据Neal-Smith准则对算例无人机系统的纵向飞行品质进行评定,结果如表4和图4所示.

表4 Neal-Sm ith准则飞行品质评定结果(着陆阶段)

图4 Neal-Smith准则飞行品质评定结果图(着陆阶段)
由表4和图4可知,τd对最大谐振|θ/θc|max和驾驶员补偿相角φp的影响均较大.τd增大时,由于人机闭环θ频域响应的相角变小,为使闭环带宽ωB满足准则要求,驾驶员的超前补偿需增大,进而使得φp增大,操纵负担增加.此外,τd增大还会导致|θ/θc|max增大,人机闭环响应的振荡或超调倾向增强.当 τd较大时,由于|θ/θc|max过大,且φp较大,无人机系统的纵向短周期飞行品质会发生明显降级,并会具有强烈的PIO倾向.
4 人机闭环仿真实验
根据无人机系统模型(图1),采用式(1)所示的无人机飞行员模型(模型参数参照Neal-Smith准则确定),对“无人机飞行员-无人机系统”人机闭环系统在执行俯仰角θ阶跃跟踪任务时的飞行进行数学仿真模拟.当人机闭环系统的闭环带宽为ωB=2.5 rad/s时,仿真结果如图5所示.

图5 人机闭环仿真结果(ωB=2.5 rad/s)
由图5可看出,为确保人机闭环θ响应的上升时间较小(即满足 ωB=2.5 rad/s),τd增大时,θ响应的振荡和超调现象会加剧.当τd较大时(如0.5 s),无人机人机闭环系统在执行θ阶跃指令跟踪任务时会进入持续的振荡之中,进而发生PIO现象.这与本文前述PIO趋势预测结果是一致的.
在执行慢机动飞行任务时(取ωB=1.5 rad/s),人机闭环飞行仿真结果如图6所示.

图6 人机闭环仿真结果(ωB=1.5 rad/s)
由图6和图5可看出,当ωB=1.5 rad/s时,人机闭环θ响应的上升时间较ωB=2.5 rad/s时增大(快速性下降),但超调和振荡明显减弱;τd较大时(如0.5 s),人机闭环系统在执行θ阶跃指令跟踪任务时无PIO现象发生.这表明,τd较大时,无人机人机闭环系统在执行慢机动飞行任务时(即ωB相对较小),不会发生PIO现象.
综上,τd较大时,算例无人机人机闭环系统具有发生PIO的倾向,且在执行快速机动飞行任务(即ωB较大)时,可能发生PIO现象,在执行慢机动飞行任务时,则不会发生PIO现象.
5 结论与建议
本文参照部分有人机飞行品质准则,建立了适用于遥控模式下无人机系统的纵向飞行品质评定方法,可较全面考察无人机系统的短周期飞行品质特性,并可对其PIO趋势进行预测.对算例无人机系统在遥控模式下的纵向飞行品质进行了评定及分析,得到以下结论:
1)通过飞控系统的调节作用,无人机系统可具有良好的短周期频率和阻尼等特性,且这些特性主要取决于无人机平台.
2)通信数据链时延会增大无人机系统的延迟时间,使人机闭环响应的快速性下降,振荡或超调等不利倾向增强,对短周期闭环操纵品质具有不利的影响,并可能导致其发生降级.
3)通信数据链时延会增强无人机系统的PIO趋势.通信数据链时延较大时,遥控模式下的无人机系统会具有较强烈的PIO趋势,且在执行快速机动飞行任务时,可能发生PIO现象.
4)采用本文推荐的各种准则来评定遥控模式下无人机系统的纵向飞行品质时,得到的飞行品质变化规律是一致的.
对此,本文提出以下建议:
1)在设计过程中,尽可能降低通信数据链等模块的延迟时间,以降低无人机系统的延迟时间.
2)采用时延补偿技术,根据无人机响应的实时预测来修正地面控制站的输出信息,减小无人机飞行员感受到的时间延迟,改善操纵感觉[2-3].
3)尽可能避免无人机在遥控模式下执行快速机动飞行任务,以避免发生PIO现象.
References)
[1]陶于金,王建培.无人机飞行品质标准研究[J].飞行力学,2010,28(1):13 -15 Tao Yujin,Wang Jianpei.Research on flying qualities criteria of the unmanned aerial vehicle[J].Flight Dynamics,2010,28(1):13-15(in Chinese)
[2] Thurling A J,Greene K A.An improved predictive algorithm for time delay compensation in UAVS[R].AIAA 2001-4424,2001
[3]丁团结,方威,王锋.无人机遥控驾驶关键技术研究与飞行品质分析[J].飞行力学,2011,29(2):17-19 Ding Tuanjie,Fang Wei,Wang Feng.Development of UAV remote-piloted key technology and flight qualities[J].Flight Dynamics,2011,29(2):17 -19(in Chinese)
[4] Holmberg JA,King D J,Leonard JR.Flying qualities specifications and design standards for unmanned air vehicles[R].AIAA 2008-6555,2008
[5] Cárdenas EM,Boschetti P J,Amerio A.Stability and flying qualities of an unmanned airplane using the vortex-lattice method[J].Journal of Aircraft,2009,46(4):1461 -1464
[6] Howard R M,Bray R M,Lyons D F.Flying-qualities analysis of an unmanned air vehicle[J].Journal of Aircraft,1996,33(2):331-336
[7] Cottingy M C.An initial study to categorize unmanned aerial vehicles for flying qualities evaluation[R].AIAA 2009-307,2009
[8] MIL-STD-1797 A flying qualities of piloted aircraft[S]
[9]高金源,李陆豫,冯亚昌,等.飞机飞行品质[M].国防工业出版社,2003 Gao Jinyuan,Li Luyu,Feng Yachang,et al.Aircraft flying qualities[M].Beijing:National Defense Industry Press,2003(in Chinese)
[10]宁国栋,方振平.Neal-Smith时域PIO预测准则及应用[J].北京航空航天大学学报,2005,31(4):407-451 Ning Guodong,Fang Zhenping.Time domain Neal-Smith criterion and PIO prediction[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(4):407 - 451(in Chinese)
