ABAQUS中三维梁单元材料单轴本构模型的二次开发

袁伟泽，陈清军

(同济大学土木工程防灾国家重点实验室，上海200092)

有限元在钢筋混凝土结构分析中已得到广泛应用。我国抗震规范中已规定，应采用弹塑性分析方法计算罕遇地震下结构的变形，对于复杂结构还应采用有限元方法进弹塑性时程分析。大型通用有限元软件ABAQUS是目前国际上功能强大的有限元软件之一，可以模拟包括结构分析、热传导等多方面的非线性问题，同时它具有良好的开放性，提供了多种二次开发的接口，方便用户根据需要扩展它的功能。

ABAQUS软件提供的混凝土本构模型主要有塑性损伤模型和弥散裂缝模型［1］。塑性损伤本构模型是Lee和Fenves［2］于二十世纪九十年代提出来的，该模型用损伤变量来模拟裂缝的开裂、发展所引起的材料刚度和强度的退化，通过受压、受拉损伤变量来分别描述混凝土材料的受压损伤和受拉损伤，同时采用非关联塑性模型来模拟混凝土的塑性膨胀，由刚度回复参数模拟混凝土裂缝的开裂和闭合。然而，该模型可结合实体单元及分层壳单元进行混凝土结构弹塑性分析，却不支持空间梁单元的塑性计算。弥散裂缝模型可用来模拟混凝土断裂及断裂后行为，它是将裂缝分布到整个结构中，通过刚度退化或强度降低来反映裂缝的影响;该模型虽可以用于三维梁单元的弹塑性分析，但难以对结构进行强非线性分析且计算收敛性较差。为了完善ABAQUS软件模拟钢筋混凝土三维梁单元的弹塑性本构模型，本文基于混凝土和钢筋的材料本构理论，开发了混凝土和钢筋的单轴本构滞回模型，以满足钢筋混凝土结构弹塑分析的需要。

1 基于ABAQUS软件的二次开发

ABAQUS在隐式求解器Standard和显式求解器Explicit中分别提供了子程序 UMAT接口和VUMAT接口。UMAT接口可利用主程序传入的应变增量和状态变量(历史最大应、变塑性应变等)，求解应力增量，返回雅各比矩阵给主程序以形成整体刚度矩阵，并存储状态变量，然后进行下一增量步的求解［3］。VUMAT接口的原理与UMAT接口基本相同，但由于VUMAT接口基于显式算法，在增量步中无需进行平衡迭代和返回雅各比矩阵。本文将利用基于隐式求解器Standard的UMAT接口进行二次开发。

1.1 混凝土单轴本构滞回模型

受压骨架曲线:大量研究表明，钢筋混凝土梁柱构件中的箍筋不仅明显地提升了被约束混凝土的轴心抗压强度，而且大大提高了构件的延性耗能能力。本文的混凝土受压骨架曲线采用20世纪80年代Mander［4］提出的考虑箍筋约束作用的应力—应变模型，该模型受压骨架曲线上升段、下降段采用统一的表达式，在数值计算过程中更加方便，计算稳定性也较高，且计算结果与试验结果吻合较好。同时在本文的模型中，为了提高计算效率，当混凝土的应变小于2/3倍的峰值应变时，应力计算简化为弹性，混凝土的受压骨架曲线为

式中σc－压区骨架曲线上的应力;σcc－峰值应力;εcc－峰值应力处的应变;r=E(E－Esec);E－初始弹性模量，Esec=σcc/εcc。

受压卸载－再加载滞回模型:当卸载点应变ε≤2εcc/3时，混凝土按照弹性模量卸载和再加载。当卸载点应变ε＞2εcc/3时，混凝土的卸载和再加载曲线采用清华大学过镇海等［5］结合试验研究结果给出的滞回模型，该模型的表达式简单，计算效率较高，且计算准确度相对较高。关于卸载应力为0时残余应变的计算问题，本文利用齐虎等［6］通过整理已有试验数据，建议的简化计算进行计算。

受拉骨架曲线:国内外很多学者针对混凝土的受拉应力应变曲线提出了很多种不同的表达形式，有单直线模型、双直线模型、三直线模型、曲线直线模型、曲线模型等。然而为了提高计算效率，本文采用与《混凝土结构设计规范》给出的混凝土受拉骨架曲线符合较好的双直线本构模型，其表达式为

式中σt－拉区骨架曲线上的应力;σtp－峰值应力;εtp－峰值应力处的应变;εtu－极限应变。

受拉卸载－再加载滞回模型:由于反复荷载作用下，混凝土的抗拉强度对截面承载力的贡献较小，所以关于混凝土卸载－再加载滞回模型的研究不多。依据受拉骨架曲线，当卸载点应变ε≤εtp时，按照弹性模量卸载和再加载，当卸载点应变ε＞εtp时，按照考虑混凝土所有受拉应力－应变加载情况的滕智明模型［7］确定卸载－再加载曲线。

综合以上分析，对于混凝土本构单轴滞回模型的受压部分，主要采用考虑箍筋作用的Mander受压骨架曲线和表达式简单、计算效率较高的过镇海加卸载滞回模型，对于受拉部分主要采用双线型的骨架曲线和考虑受拉贡献和裂面效应的滕智明［7］加卸载滞回模型。本文的混凝土单轴本构模型在复杂加载路径下的滞回曲线如图1所示。

1.2 钢筋的单轴滞回本构模型

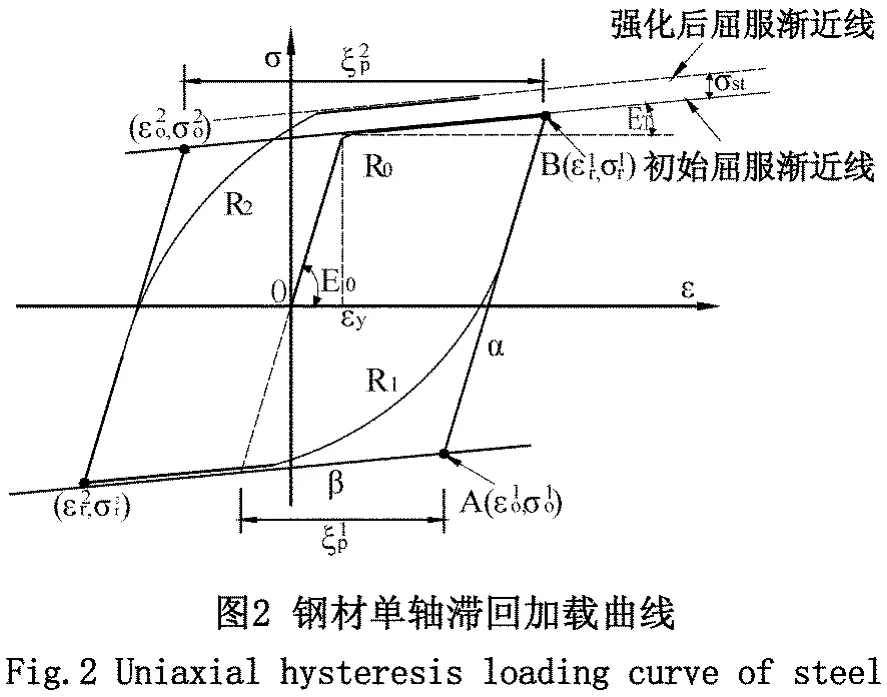
本文采用的钢筋单轴本构模型与美国太平洋地震工程研究中心开发的OpenSEES中的Steel02模型相同。该本构模型最早提出于上世纪70年代，后经Filippou等人［8］修正，可以考虑钢材等向应变硬化的影响，如图2所示。同时，由于该本构模型采用了应变的显函数表达形式，因而数值计算效率非常高，并且保持了与钢筋反复加载试验结果非常好的一致性。通过设置材料参数来改变双线性模型中弹塑性段分支点附近的弧度变化，可以反映Bauschinger效应。

2 计算结果的试验验证

由于钢筋混凝土构件的滞回行为比较复杂，本节将首先模拟一系列钢筋混凝土受弯构件的往复加载试验，在此基础上再对钢筋混凝土框架结构的试验进行模拟，以验证材料本构模型的合理性和有效性。

2.1 钢筋混凝土构件的结果对比

采用1997年日本的 Takemura和 Kawashima［9］完成的一组6个试件的拟静力试验为基础，验证本文模型对不同加载制度下钢筋混凝土受弯构件力学行为模拟的有效性。6个试件为尺寸与配筋构造均完全相同的钢筋混凝土悬臂柱，但加载制度不同。截面尺寸为400 mm×400 mm，截面有效高度h0=320 mm，加载点至地梁底面距离为1 245 mm，剪跨比为3.46，混凝土强度约为30 MPa，纵筋采用D13钢筋，屈服强度372 MPa，全部纵筋配筋率为1.66%。箍筋采用D6钢筋，屈服强度为363 MPa，箍筋间距为70 mm，配箍率为0.2%。试验时柱顶施加150 kN的轴压力，轴压比约为0.03。试验中采用了6种不同的加载制度，本文选择其中的两种有代表性的加载模式，对应的构件加载编号为TP002和TP004，如图3所示。

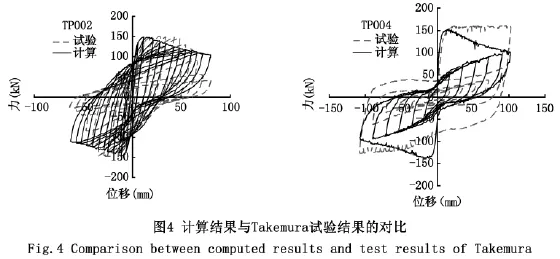
采用本文数值模型得到的计算结果与实验结果的比较如图4所示。由图4可知，对于试验中不同的加载制度，数值模型与试验所得的滞回曲线基本一致，说明采用本文的材料本构模型能够较好地把握钢筋混凝土构件的弹塑滞回行为。

2.2 钢筋混凝土框架结构的结果对比

通过模拟同济大学邹翾和周德源［10］进行的两个3层单榀钢筋混凝土框架结构反复加载试验来检验本文模型在模拟多层框架结构中的表现。

试验中两榀平面框架模型的净高和层高均相同，跨度分别为2 280 mm和3 600 mm。试件截面尺寸及配筋见文献［10］。模型中纵筋采用II级钢筋、箍筋采用I级钢筋，混凝土为C30级细石混凝土。在试验过程中，首先施加竖向荷载且在试验中保持不变，然后在水平方向采用力、位移混合控制加载制度，即在试件屈服前采用力控制，从10 kN开始，每级增加10 kN，每级推拉循环1次，至40 kN结束荷载控制阶段，之后采用位移控制，每级增加10 mm，每级推拉循环 2次，直至结构破坏。

图5给出了本文模型的计算分析结果与两个试件的滞回曲线试验结果的对比。由图5可知，试件在往复荷载作用下的延续较好，且本文模型的计算结果与试验结果的初始刚度、最大承载力及延性变化规律基本一致。说明采用本文的材料本构模型能够较好的把握钢筋混凝土结构的弹塑性滞回行为。

3 结语

本文借助于非线性有限元分析软件ABAQUS，开发了适用于三维纤维梁单元的混凝土和钢筋的单轴本构滞回模型，并对Takemura等人钢筋混凝土构件和邹翾等人框架结构的低周反复加载试验进行了模拟对比分析。结果表明，本文开发的材料单轴本构滞回模型具有良好的精度和收敛性，能够比较准确地模拟不同往复加载制度下钢筋混凝土构件及结构在刚度和承载力退化方面的滞回行为。

［1］庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用［M］.北京:清华大学出版社，2008.

［2］LEE J，FENVES G L.Plastic－damage model for cyclic loading of concrete structures［J］.Journal of Engineering Mechanics，1998，124(8):892 －900.

［3］ABAQUS .ABAQUS user manual version 6.10［M］.Rhone Island:Pawtucket，2010.

［4］MANDER J B，PRIESTLEY M J N，PARK R.Observed stress－strain behavior of confined concrete［J］.Journal of Structural Engineering，1988，14(8):1827 －1849.

［5］过镇海，张秀琴.混凝土应力－应变全曲线的试验研究［J］.建筑结构学报，1982，3(1):1－12.

［6］齐虎，李云贵，吕西林.箍筋约束混凝土单轴滞回本构实用模型［J］.工程力学，2011，28(9):95－102.

［7］滕智明，邹离湘.反复荷载下钢筋混凝土构件的非线性有限元分析［J］.土木工程学报，1996，29(2):19－27.

［8］FILIPPOU F C，POPOV E P，BERTERO V V.Effects of bond deterioration on hysteretic behavior of reinforced concrete joints［R］.Earthquake Engineering Research Center，College of Engineering University of California Berkeley，California，1983.

［9］TAKEMURA H，KAWASHIMA K.Effect of loading hysteresis on ductility capacity of reinforced concrete bridge pier［J］.Journal of Structural Engineering，Japan，1997，43A:849－858.

［10］邹翾，周德源.3层钢筋混凝土框架结构反复加载试验分析［J］.四川建筑科学研究，2005，31(2):7－11.

(责任编辑刘存英)