减震结构非线性时程分析的研究

黎超敏，崔荣乐

(1.上海大学 土木工程系，上海200072，2.淮坊市建筑设计研究院有限责任公司，山东 淮坊261000)

随着近年来世界性地震的频发，尤其是地震的强度、烈度都较以前加大不少，世界各国对建筑抗震减震越来越重视。然而建筑结构减震控制相较于一般的抗震加固无论是在抗地震强度，还是计算理论，施工等方面都有大幅度的进步，因此，建筑结构减震已经成为抗震工程界一项新的研究。

被动控制的实现有三种途径:一是通过在结构的特定部位设置水平柔性层装置，来阻断建筑结构的能量输入，从而达到减震控制的目的，即通常所说的隔震;二是通过附加在结构上的一些耗能阻尼器，如粘滞液体阻尼器、粘弹性阻尼器、金属屈服阻尼器和摩擦阻尼器等来耗散地震能量达到减震的目的，通常称之为消能减震;三是通过振动模态间的相互传递(如调谐质量阻尼器)将建筑结构的主振动转移到附加系统中去，从而达到减震的目的。

1 减震结构非线性时程分析难点

1.1 计算的理论依据及不足

层间剪切模型是把横梁视为绝对刚性，各层质量集中在屋面和楼板高度的一种模型。当多质点层间剪切结构中附设粘滞阻尼器后，可得如下所示的运动方程

式中M、K、C－结构的质量、刚度、阻尼矩阵;F(t)－作用力矩阵，对于地震作用F(t)=－M{1}¨ug;FD(u)－附加的阻尼力矩阵;u、˙u、¨u－结构的位移、速度和加速度矩阵。

当结构设置阻尼器处于弹性状态，恢复力项Ku为弹性，当结构振动进入弹塑性阶段，则恢复力项Ku也呈非线性。经过相应的数学变换，可得运动微分方程

即:如果假设结构具有粘滞阻尼，结构附加线性粘滞阻尼器后，减震结构的阻尼矩阵等于结构阻尼矩阵和附加阻尼矩阵之和。

进行时程分析时，采用Newmark方法对式(2)进行数值积分。所谓Newmark方法，就是 Newmark在1953年提出的位移关于速度，加速度的迭代方程式(3)和(4)，最终可以解得位移

从上述减震结构和非线性时程分析的基本理论中，我们不难发现有几点不足。一是对于减震结构，结构的阻尼矩阵难以确定，尤其是增加消能元件后，阻尼变化难以得知;而且除了增设的是粘滞液体阻尼器，其它类型的阻尼器，将会对结构的质量阵和刚度阵产生影响。另外，时程分析时，无论采用哪一种积分方式，都会存在一个选取积分步长的问题，如果步长太小，计算机所要存储的数据过多，负荷过大;步长太小，可能无法达到精确解;步长如果太接近结构的自振周期，又将可能导致积分式不收敛。

1.2 消能元件材料的研究

本文所述阻尼器为非线性粘滞液体阻尼器，其核心材料为粘性液体。流体分子之间存在相互吸引的内聚力，流体和固体之间又作用附着力，流体能承受较大的压应力，却几乎不能承受拉应力，对剪切应力的抵抗极弱。粘性流体材料滞回曲线所包围的面积越大，其耗能能力越强。

粘滞液体阻尼器属于速度相关型消能器，它产生的阻尼力与速度有关，当活塞杆向左推时，左侧腔体内的液体阻尼材料通过活塞头中的孔和活塞与缸壁间的缝隙流向右侧腔体，并产生作用力，此作用力与液体的流动速度有关，流速越快，产生的力越大。

虽然粘滞阻尼器能够给结构提供很大的阻尼，而且对自振周期，质量刚度没有影响，但是也有其致命缺点:一是阻尼器的粘滞系数容易受温度的影响，温度越高粘滞系数越低，耗能能力越差，而地震时，所产生的温度一般都很高，所以阻尼器非常容易受影响;二是粘滞阻尼器的加工制作比较难，粘滞液体容易泄露;三是阻尼器受安装方式的影响较大。

2 研究的创新和成果

2.1 工程案例

本文将通过一个工程案例，来研究减震结构相较无控结构进行非线性时程分析后地震作用力，基底剪力，层间位移角的比较。

工程案例为6层单跨钢筋混凝土框架－剪力墙结构，7度设防，建筑场地为II类，设计地震分组为第二组。层高为3.6 m，总高度为22.5 m;横向框架为单跨，柱距6.6 m，纵向框架为五跨沿结构第一跨和第四跨柱边通高布置剪力墙，宽为1 m，厚度 0.2 m。柱、墙、板混凝土均为 C25。Sap2000建模轴测图如图1。

2.2 设计规范的修订

《建筑抗震设计规范》(GB50011－2010)第十二章对房屋消能减震设计提出了几点设计要求，条文说明第五章对时程分析和地震加速度曲线的选取提出了几点要求:

1)消能减震设计时，应根据多遇地震下的预期减震要求及罕遇地震下的预期结构位移控制要求，设置适当的消能部件。本案例中，选用阻尼系数 ，速度指数C=500(N·s/mm)，速度指数a=0.3非线性粘滞阻尼器。

2)消能部件可根据需要沿结构的两个主轴方向分别设置。根据无控结构时程分析时层间位移角过大部位，设置阻尼器。本例粘滞阻尼器布置在结构的一、二层，分别布置在x方向第一、第四跨和y方向第一、第二跨;每层4个阻尼器，一共布置8个。

3)正确选择输入的地震加速度时程曲线，满足频谱特性、振幅和持续时间均要符合规定。本案例选取两条地震波进行时程分析，分别是ELCentro波和Taft波。

EL－Centro地震波，峰值加速度amax=341.7gal(gal=cm/s2)。持续时间为53.6 s，本文选取前30 s作为输出结果。

Taft地震波，时间间距为 0.02 s，持续时间52.002 s，本文选取前30 s作为输出结果，峰值加速度amax=175.95 gal。

4)关于非线性时程分析的几点说明:结构的阻尼比取为0.05，满足《抗规》(GB50011－2010)5.1节的相关规定。结构动力时程分析的总持时为30 s，远远大于结构自振周期的10倍，满足《抗规》中大于自振周期5－10倍的要求;时程分析时时间步长取为0.02 s，与地震波间隔相同，满足规范要求。

3 研究的成果

顶层位移的比较见表1。

在两条地震波作用下，多遇地震、设防地震、罕遇地震下减震结构顶层位移的峰值均有不同程度的减小。多遇地震情况下，减震结构顶层位移峰值减小最大，每条地震波作用下基本都减小了五成，相对来说罕遇地震作用下，每条地震波作用下都降低了两成左右，见图2、图3。层间位移角对比见图4。

El－Centro波和Taft波作用时，层间位移减震率跨度较大;EL－Centro波作用时，X向的层间位移角减震率为38.2% －71.0%，Taft波作用时，X向的层间位移角减震率为25.6% －84.2%。层间位移角在2，3，5层均有放大的趋势，从图像来看，减震结构的层间位移角相对无控结构的要更加平滑、弧度更加圆润、饱满。柱轴力对比见表2。

从以上分析可以看出，在EL－Centro波、Taft波作用时，消能结构的减震效果明显，柱轴力明显减小，减震率基本都能达到三成。另外，柱轴力减震率最大值基本都出现在了结构的底层和第二层，即结构装设粘滞液体阻尼器的地方。可见，装设粘滞阻尼器对减小柱内力有很大的效果。

表1 EL－Centro波顶层最大位移变化情况Tab.1 Max displacement of top floor of El－ Centro

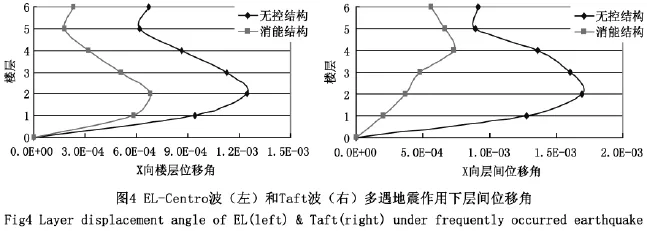
表2多遇地震作用下柱的最大轴力Tab.2 Max axial force of column under frequently occurred earthquake

4 结论

1)对于装设了粘滞液体阻尼器的消能结构，无论是顶层最大位移、层间位移角还是柱内力，消能结构的地震作用响应总是小于无控结构;而消能结构层间位移角表现的更加圆滑，弧度更加饱满，可以理解为装设了阻尼器后，使结构的层间位移更为均匀。

2)粘滞阻尼器对其所在层的层间位移降低最大，而且粘滞阻尼器对上邻近层的位移控制效果要比对下部邻近层的位移控制效果好。本文将阻尼器设置在底层和第二层，减震效果显著。可见，当两层的层位移基本一致时，设置在较低楼层减震的效果更好。

3)通过无控结构和消能减震结构的地震反应对比，粘滞阻尼器通过粘滞耗能，不仅使结构的位移，而且也使结构构件的受力情况也得到了很大的改善。

［1］GB50011－2010，建筑抗震设计规范［S］.

［2］张思海.被动耗能减震结构基于性能的抗震设计方法［D］.西安:西安建筑科技大学硕士学位论文，2005.

［3］刘鹏飞.刘伟庆.基于位移的减震结构设计方法研究［J］.世界地震工程.2009，25(1):43－47.

［4］李钢，李宏男.基于位移的消能减震结构抗震设计方法［J］.工程力学，2007，24(9):88－94.

［5］隋杰英.姚幸海.抗震加固用消能减震结构的弹塑性时程分析研究［J］.固体力学学报，2006，27:87－92.

［6］林新阳，周福霖.消能减震的基本原理和实际应用［J］.世界地震工程，2002，18(3):48－51.

［7］FEMA273，274.NEHRP Commentary on the guidelines for the rehabilitation of building［M］.WashingD C，Federal Emergency Management Agency，1996.

［8］M C.Constantinous，principle of friction，viscoelastic，yielding steel and fluid viscous dampers［J］.Properties and Design，Passive and Active Structural Vibration Control in Civil Engineering，1994:209 －240.