混合FEM-FIPWA求解复杂旋转体散射
2013-03-18柳清伙
芮 锡,胡 俊,柳清伙
(1.中国西南电子技术研究所,成都610036;2.电子科技大学电子工程学院,成都610054;3.杜克大学电气和计算机工程学院,达勒姆27708,美国)
混合FEM-FIPWA求解复杂旋转体散射
芮 锡1,胡 俊2,柳清伙3
(1.中国西南电子技术研究所,成都610036;2.电子科技大学电子工程学院,成都610054;3.杜克大学电气和计算机工程学院,达勒姆27708,美国)
提出了一种基于混合有限元与快速非均匀平面波算法求解复杂旋转体的散射问题。内部电场采用基于点元和边元基函数的有限元方法计算,同时在旋转体的外表面的场采用基于三角基函数及脉冲基函数的快速非均匀平面波算法计算。采用这种方法处理复杂大尺度的旋转体问题能节省计算的内存和计算时间,算例验证了算法的准确性和有效性。
复合材料;旋转体;电磁散射;快速非均匀平面波算法;有限元法
1 Introduction
The electromagnetic problem for bodies of revolution(BOR)of arbitrary shapewith different kinds ofmaterials has been widely discussed for several decades[1-6].In thiswork,FEM-BI is presented to analyze the scattering of BOR with inhomogeneousmaterials,and extend the fast inhomogeneous plane wave algorithm to accelerate the computation of themethod ofmoment(MoM).Finite ElementMethod(FEM)isused to analyze the interior electric field.Edge-based and node-based elements are used to represent the interior electric field.While for the exterior region,Boundary Integration(BI)is used as a exact boundary condition.Triangular and pulse basis functions are used to represent the electric and magnetic fields on the boundary.The aggregation and disaggregation factors in Fast Inhomogeneous Plane Wave Algorithm(FIPWA)can be derived analytically.Both thememory requirement and the CPU time are saved for large scale BOR prob-lems.Numerical results are given to demonstrate the validity and the efficiency of the presented method.
2 FEM-FIPWA for Axisymmetric Resonators
2.1 Body of revolution
Because of the symmetry of the geometry,the volume of the BOR is generated by revolving a plane curve about the z-axis as shown in Figure 1.Here(ρ,φ,z)are the variables in cylindrical coordinate system,θincis the angle of incidentwave,^t and^φare the unit vectors,S is the surface of the BOR.

Fig.1 Body of revolution and coordinate system图1 旋转体结构坐标系统
The electric and magnetic fields can be expressed in a Fourier series:

where Et,m,Eφ,m,Ht,mand Hφ,mare the electric and magnetic fields in the meridian plane and the azimuthal component of the m-th Fourier mode,respectively.As the fields are decomposed into two parts as shown in E-quation(1-2),only a 2-Dmesh(meridian cross section)is needed for analyzing the3-D axisymmetric problem.These differentmodes can be treated separately because of the orthogonality.In the cylindrical coordinate system,the unit vectors^t and^φare defined as whereθis the angle between the z-axis and the unit vector^t.φis the azimuthal angle as shown in Figure 1.

2.2 FEM for the interior region
As shown in Figure2,the interior region of the BOR is filled with inhomogeneous material with the relative permittivityεrand the relative permeabilityμr.Bothεr andμrare the function of z andρ,but independentofφ.

Fig.2 Themesh for the interior and exterior regions图2 内部区域与外部区域的网格划分
The vector Helmholtz equation for the electric field can be written as

where Seis the source term,and k0is the wave number in free space.If it is source free(Se=0)in the interior region the weak form of the vector wave equation can be expressed as[7-8]

where Wlis the testing function,andμ0is the permeability of the free space.
The fieldsmust retain the continuity for any values of φon the z-axis(ρ=0).Thus,there are three kinds of conditions for different cylindricalmodes:

The basis functions for the electric field are chosen as
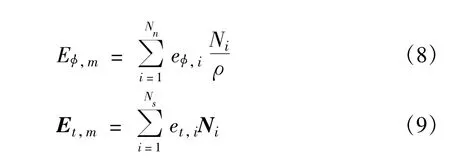
where Nnis the number of nodes,Nsis the number of segments(or edges),et,iand eφ,iare the unknown coefficients,and Niand Nirepresent the standard node-based and edge-based element basis functions,respectively. Themagnetic field on the boundary S is expanded as the same as the electric field.

The testing function is chosen as
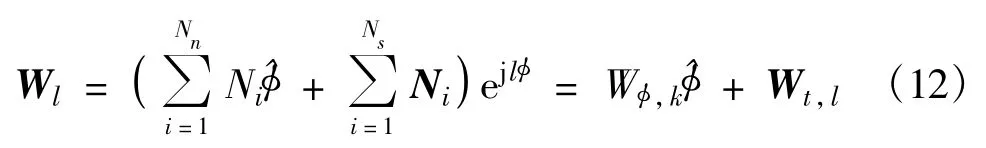
After substituting the basis and testing functions into Equation(6)and making use of the orthogonality of cylindricalmodes,the wave equation can be rewritten as

can be formed,where m is the index of themode and b is the index of boundary.And thematrix element can be expressed as


2.3 FIPWA for the exterior region
For the exterior region,boundary integration is applied to govern the boundary electricfield E andmagnetic fields M.The fields on the boundary S can bewritten as
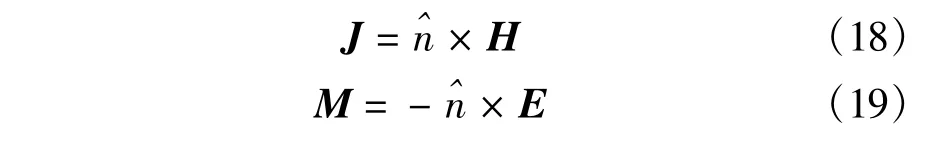
where J and M are the equivalent electric and magnetic currents,which will satisfy the electric field integral equation(EFIE)and the magnetic field integral equation(MFIE)

where G is the Green′s function,and the integration in the equation above has remove the contribution of the singular point.The key process of MoM is solving themodal Green′s function gnwhich can be expressed as
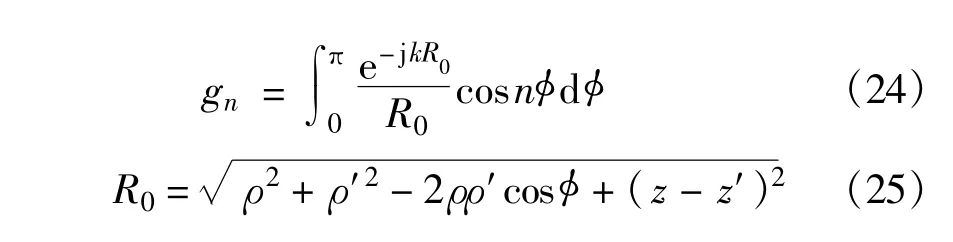
For the traditionalMoM,themodalGreen′s function has to be evaluated by numericalmethod,hence it is time consumingwhen the radius of the BOR is large.In this section,fast inhomogeneous plane wave algorithm(FIPWA)is applied to accelerate the computation of the MoM for bodies of revolution.Based on Weyl Identity[9-10],the Green′s function can be expressed as

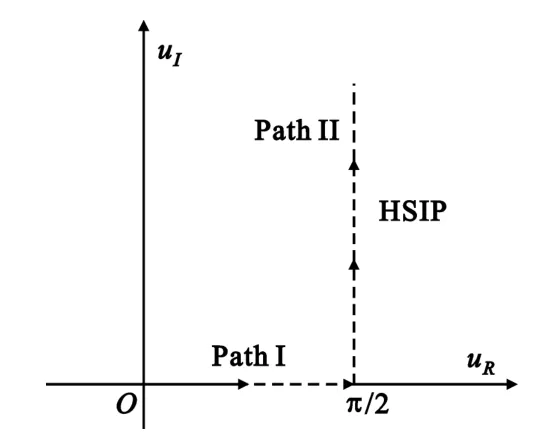
Fig.3 The Sommerfeld integration path on the complex u plane图3 复平面上的Sommerfeld积分路径
In order to realize the Fast Inhomogeneous Plane Wave Algorithm(FIPWA),the basis functions are divided into groups.Herewe call rmand rm′are the centers of the groups which contain the source point rjand field point rirespectively.As shown in Figure 4,rji=rjm+rmm′+rm′i.Equation(26)can be rewritten as

Fig.4 The field point and the source point图4 场点与源点位置分布
The basis functions are divided into M groups along the z direction as shown in Figure 5.In this way,the factor rmm′has z component only.This character will make the integrand decay exponentially away from the real axis in the complex u plane.

Fig.5 The BOR is divided into groups图5旋转体分组示意图
Equation(26)can be rewritten as
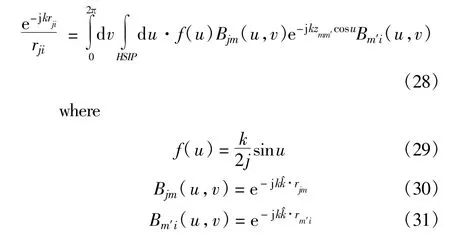
Here the Bjm(u,v)and Bm′i(u,v)represent the radiation and receiving patterns for the field and source groups,respectively.And f(u)can be considered as the weight function.Both Bjm(u,v)and Bm′i(u,v)are the inhomogeneous planewave as u is complex.With proper numericalmethods for u and v,the integral can be expressed as

The detail of the FIPWA can be found in Reference[5-6].
2.4 FEM-FIPWA for BOR
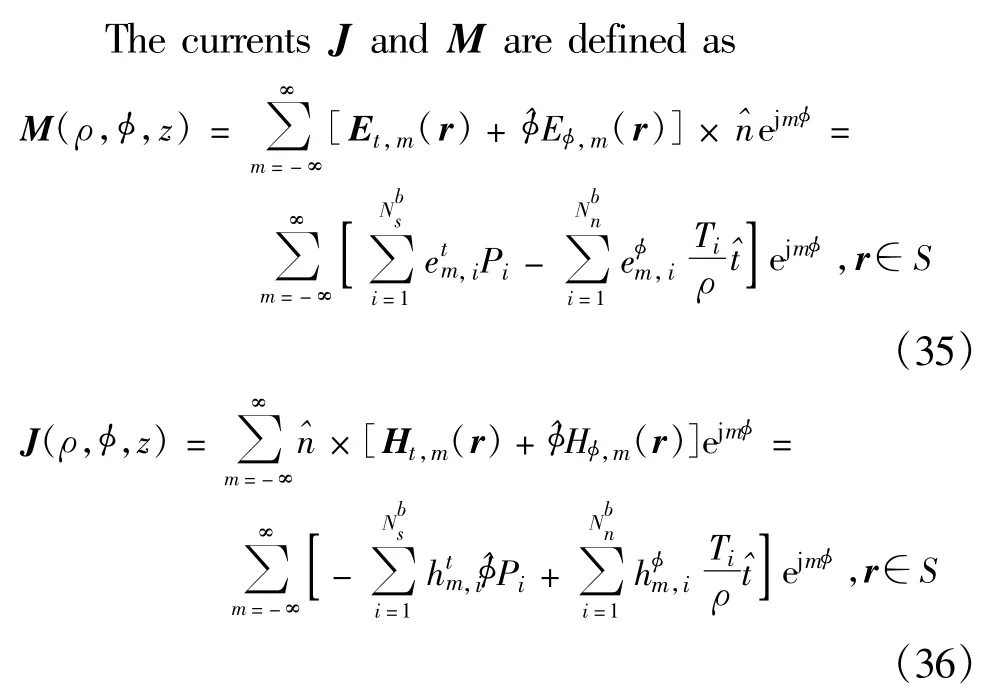
where Piis the pulse basis function and Tiis the traditional triangle basis function.Combining the FEM part(interior region)and FIPWA(boundary),thematrix equation can be derived as

The details of thematrix elements can be found in Reference[4-6].The boundary currents and fields can be derived by solving the equation above,and the far field also can be solved.In the next section,two numerical results will be given to demonstrate the validity and the efficiency of the proposed method.
3 Numerical Results
In this section,two numerical results are presented to show the validity of the proposed FEM-FIPWA method.All problems are solved on the same computer(Intel Core2 DuoCPU P8400@2.26GHz with 1.92GB RAM)in order to make a fair comparison,with only one core being used.
3.1 An inhomogeneous dielectric sphere with two layer medium
As shown in Figure 6,an inhomogeneous dielectric sphere is computed.The sphere isexcited by the planewave with horizontal polarization(θinc=00,φinc=00,λ=2 m). The total number of the unknowns is about 40 000.The bistatic RCS is shown in Figure 7,the resultof FEM-BI(or FEM-FIPWA)agreeswellwith analytical result.
Fig.6 An inhomogeneous dielectric spherewith two-layermedium图6 非均匀双层介质球结构
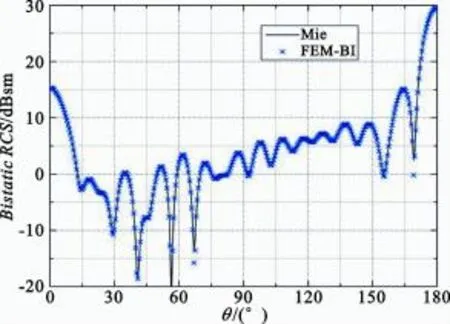
Fig.7 The bistatic RCSof the dielectric sphere result by FEM-BIcompared with analytic result图7 介质球双站RCS的计算结果比较图
3.2 An inhomogeneous dielectriccylinder
The numerical result proposed above shows the accuracy of FEM-FIPWA for BOR problems.In this section,a more complex example is shown to verify the efficiency of proposedmethod mentioned in this paper.As shown in-Figure 8,there are seven layeredmedium.The thickness of the six inner medium is 0.2m and the height is 2.6m.The thickness of the outermedium is0.3m,and the height is 2m.The cylinder is excited by the plane wavewith horizontal polarization(θinc=90°,φinc=0°,λ=0.5m).The number of the total unknowns is morethan 100 000 in this2-Dmesh.The field distribution derived by FEM-BI is compared with Wavenologywhich is a famous commercial EM software in USA.As shown in Figure 9,the results agree wellwith each other.

Fig.8 The geometry of the inhomogeneous dielectric cylinder图8 非均匀介质柱结构图
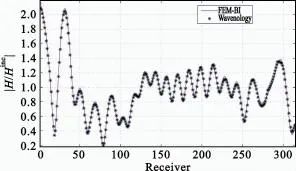
Fig.9 The field distribution of the dielectric cylinderwith two differentmethods图9 两种方法计算介质柱的场分布结果比较
As shown in Table 1,thememory requirements and CPU times for FEM-MoM and FEM-FIPWA are compared.

Table 1 The comparison between FEM-MoM and FEM-FIPWA表1 FEM-MoM与FEM-FIPWA计算比较
4 Conclusion
In this paper,hybrid FEM and FIPWA technique is applied to solve the BOR scattering problem.In this FEM-FIPWA method,the problem is separated into interior and exterior problems.In the interior region,FEM based on hybrid edge-based and node-based elements is used to present the electric field.In the exterior region,boundary integration(BI)is used as the exact boundary condition.Triangular and pulse basis functions are used for representing the electric and magnetic fields on the boundary.FIPWA is added for the BIpart.The proposed method can solve large scale bodies of revolution with inhomogeneous,compositematerials efficiently.
[1]Andreasen M G.Scattering from bodies of revolution[J]. IEEE Transactions on Antennas and Propagation,1965,13(2):303-310.
[2]Mautz JR,Harrington R F.Electromagnetic coupling to a conducting body of revolution with a homogeneous material region[J].Electromagnetics,1982(2):257-308.
[3]Medgyesi-Mitschg LN,Putnam JM.Electromagnetic scattering from axially inhomogeneousbodiesof revolution[J].IEEETransactions on Antennas and Propagation,1984,32(8):797-806.
[4]RuiXi.Finite elementmethod for inhomogeneous axisymmetric resonators[J].Telecommunication Engineering,2012,52(1):105-110.
[5]Rui X,Hu J,Liu QH.Fast Inhomogeneous PlaneWave Algorithm for Scattering from PECBody of Revolution[J].Microwave and Optical Technology Letters,2010,52(8):1915-1922.
[6]Rui X,Hu J,Liu Q H.Higher order finite elementmethod for inhomogeneous axisymmetric resonators[J].Progress In Electromagnetics Research B,2010,21:189-201.
[7]Morgan M A,Mei K K.Finite-element computaion of scattering by inhomogeneous penetrable bodies of revolution[J]. IEEE Transactions on Antennas and Propagation,1979,27(2):202-214.
[8]Lee JF,Wilkins G,Mittra R.Finite-elementanalysis ofaxisymmetric cavity resonator using a hybrid edge element technique[J].IEEE Transactions on Microwave Theory Technique,1993,41(11):1981-1987.
[9]Chew W C.Waves and Fields in Inhomogeneous Media[M].New York:Van Nostrand Reinhold Co.Ltd.,1990.
[10]Hu B,Chew W C,Michielssen E,et al.Fast inhomogeneous plane wave algorithm for the fast analysis of two-dimensional scattering problem[J].Radio Sciences,1999,34(4):759-772.
Biography:

RUIXiwas born in Liyang,Jiangsu Province,in 1983.He received the B.S.degree and the Ph. D.degree from University of Electronic Science and Technology of China in 2005 and 2010,respectively.From 2008 to 2010,he has been workingwith Prof.Q.H.Liu as a visiting scholar in Duke University.He is now an engineer.His research interests include computational electromagnetic and RF stealth.
Email:uestcruixi@gmail.com
芮锡(1983—),男,江苏溧阳人,分别于2005年和2010年获电子科技大学学士学位和博士学位,2008~2010年在美国北卡州杜克大学做访问,现为工程师,主要研究方向为电磁计算与射频隐身。
Hybrid FEM-FIPWA for Scattering from Com plex Bodies of Revolution❋
RUIXi1,❋❋,HU Jun2,LIU Qing-huo3(1.Southwest China Institute of Electronic Technology,Chengdu 610036,China;
2.School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 610054,China;3.Department of Electrical and Computer Engineering,Duke University,Durham,NC 27708,USA)
A method based on hybrid finite elementmethod(FEM)and fast inhomogeneous planewave algorithm(FIPWA)is proposed to solve the electromagnetic scattering problem for bodies of revolution(BOR)with inhomogeneous,compositematerials.The FEM with mixed edge-based and node-based elements is used for representing the interior electric field,while the FIPWA is used as the exact boundary condition,hybrid triangular and pulse basis functions are used for representing the electric field and magnetic field on the boundary.Both thememory and CPU time requirements are reduced for large scale BOR problems.Numerical results are given to demonstrate the validity and the efficiency of the proposedmethod.
compositematerial;body of revolution;electromagnetic scattering;fast inhomogeneous planewave algorithm;finite elementmethod
10.3969/j.issn.1001-893x.2013.01.019
TN
A
1001-893X(2013)01-0093-06
❋Received date:2012-11-28;Revised date:2012-12-13
2012-11-28;修回日期:2012-12-13
❋❋Corresponding author:uestcruixi@gmail.com通讯作者:uestcruixi@gmail.com
