超声振动深孔珩磨振动系统的设计
2013-03-17郑挺军朱林
郑挺军,朱林
(1.中国兵器工业第213 研究所,陕西西安710061;2.西安石油大学机械工程学院,陕西西安710065)
在深孔珩磨中,将超声振动切削技术应用到的深孔珩磨工艺中,将会获得比普通珩磨优异的工艺效果,可大大提高加工精度、表面质量和效率。但是由于该技术涉及电学、声学、机械学等众多学科,知识面宽,是属于边缘学科,其声振系统的结构设计没有完整而成熟的理论公式可供参考。作者利用力学振动系统和电路系统的类比特性原理,通过试验研究,建立了超声振动深孔珩磨中挠性杆-油石座振动系统的数学模型,确定了该系统的频率方程的修正系数,为该声振系统的设计提供了较为准确的依据。
1 设计原理
当将力类比于电压、振速类比于电流、力阻抗类比于电阻抗时,力学振动系统和电路之间有等效关系,这种方法称为力电类比法。超声振动系统是一个力学振动系统,利用力电类比,可将它描述为类似电路的等效机械图,从而可应用机械阻抗方法,方便地分析其振动性能,从而为其设计带来方便。
为了设计需要,将挠性杆-油石座工具振动系统简化为端点带有集中质量的杆,其数学模型建立如下:
挠性杆-油石座工具振动系统可以简化为端点带有集中质量的杆的数学模型,设集中质量的大小为M,其纵向自由振动方程为:

式中:u 为纵向位移,m;
E 为弹性模量,Pa;
ρ 为杆的材料密度,kg/m3。
为解上述振动方程,假设杆的各点作同步运动,即设:

式中:T(t)为运动规律的时间函数;
U(x)是杆上距原点x 处截面的纵向振动幅值。
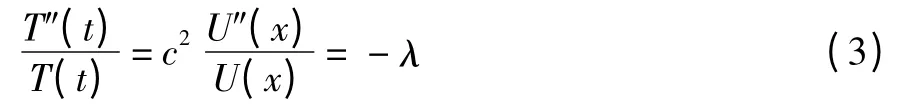
式(3)中第一个等号的左边与x 无关,右边与t 无关,λ 只能是常数,由此得到:

当λ >0 时,才有非零解U(x),设λ =ω2,其中ω 为正数。则式(4)变为

则由式(5)可以解得:
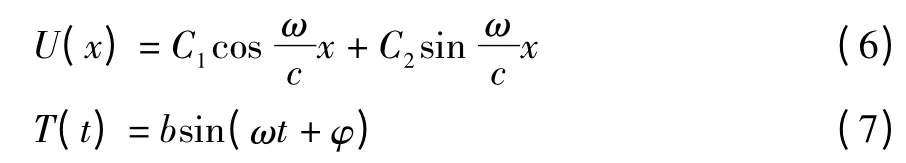
式中:C1、C2、b 为常数,ω 为固有圆频率。
根据等直杆的简单边界条件,一端固定一端自由可得

将式(8)代入式(6)解出固有频率为:

相应的主振型为:
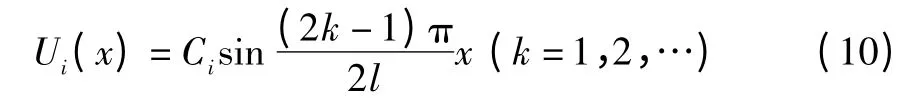
根据挠性杆的左端固定,右端有集中质量M,边界条件为:

由式(11)、(2)、(7)可得:

将式(12)代入式(6)中得

上式即频率方程,引入量纲为一的因子

式中:l 为挠性杆的长度,mm;
A 为挠性杆的横截面,mm2;
M 为油石座质量,kg。
则式(13)可写为

由式(15)可得

为了计算挠性杆-油石座振动系统,求解其频率方程(16)的解,利用计算机进行数值计算。在这里使用MATLAB 软件,它具有强大的计算和图形绘制功能,为进行数值计算带来了方便。为了求解频率方程,可以用fplot 函数在指定的范围内绘制出该函数的图形。
(1)创建M 文件myfun
function y=myfun(x)
动力有限元模型的离散参数需要根据相应地层的剪切波波速及激励的频率范围来确定[16]。为了简化模型,同时又能反映地层的动力特性,根据地层剪切波速的变化范围,将复杂的真实地层简化为5层水平构造,每层代表一个主要的剪切波速域[17]。剪切波速cs的计算公式[18]为:
y=x* tan(x)-0.36
注:根据不同的质量比α,创建不同的M 文件,程序中α1=0.36(第一次试验时的质量比)
(2)运行程序
fplot(‘myfun’,[1,10])
注:该函数的语法格式为:fplot(function,limits),.limits 是一个矢量,指定x 轴上的范围。为了求频率方程的根,在指定范围内绘制函数图形,交点的横坐标即为频率方程的根。根据设计要求,只输出范围在1 ~10 的函数图形,即频率方程的根的范围在1 ~10 之间。
(3)图形输出

图1 α=0.36 频率方程求根曲线图
(4)区间化分
根据图1 把根的区间化为[1,2]、[2,4]、[5,7]、[8,10],所求的根就在这几个范围内。
(5)选取区间
对于超声深孔珩磨声振系统的固有频率,不同的声振系统的固有频率值是不相同的,因为频率具有周期性,故同一系统在每个周期内分别还会有相应的频率值。根据声振系统的频率值应在20 kHz 左右的原则,系统设计时只要算出满足要求的频率值即可。考虑珩磨结构,主要选择[5,7]区间作为该系统设计的主要区间。其求根曲线图如图2所示。
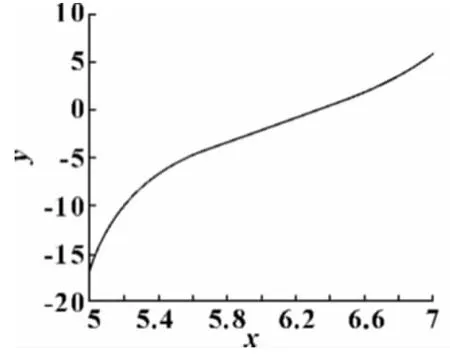
图2 [5,7]区间频率方程求根曲线图(α=0.36)

图3 [6.2,6.4]区间频率方程求根曲线图(α=0.36)
将[5,7]区间再次细化为[6.3,6.4],如图3所示,即可得到所求解,β = 6.34,将β 值代入式(14)中,可以算得挠性杆长l=270 mm。
2 试验
为上验证上述计算结果,并对其进行修正,最终得到较为合适的修正系数,则对挠性杆-油石座振动系统进行试振,根据结果对相应系数进行修改。初次试验的相应尺寸为:油石座长度L =129 mm、厚度H=12 mm、宽度B=9 mm,挠性杆直径为5 mm、长度为270 mm。
试验条件:
超声波发生器:电源输出电压220 V,输出最大功率1 000 W,工作频率为20 kHz ±400 Hz;阻抗分析仪:PV70A;
弯曲振动圆盘:厚度5.8 mm,直径96 mm;阶梯形变幅杆:调质45 钢;
换能器:压电陶瓷;
电脑、测试软件等。

图4 l=270 mm,α=0.36 测试参数
在阶梯形变幅杆与换能器、弯曲振动圆盘连接好后,将挠性杆-油石座焊接在弯曲振动圆盘上,再将这套振动系统与阻抗分析仪相连,最后与计算机相连接。其初次试验结果如图4所示。
由图4所示,谐振频率f =25.7 kHz,与理论计算相差较大,因此在不改变油石座基础上修改挠性的长度l,改变质量比α。现分别列于表1 中。

表1 挠性杆-油石座振动实验结果(油石座高度为12 mm)
由表1 可以出,理论计算结果与实验值之间存在差值,这主要是由于将油石座、油石简化为一个集中质量,而实际上油石座的形状,质量分布都会影响系统的固有频率,因此对频率方程作修正,引入修正系数K,对式(16)进行修正,修正后频率方程为:

式中:K 为修正系数,(K=0.85);
l 为挠性杆的长度,mm。
最终确定挠性杆的长度l =230 mm,直径为5 mm,将挠性杆-油石座振动系统与超声波发生器相连接,振动雾化较果好。
为了进一步验证修正系数的准确程度,再对挠性杆-油石座振动系统进行结构设计,并连接实验仪器,确定修正后计算的频率与实测频率之间误差。改变油石座高度,并在油石座上铣出油石槽,其结构如图5所示。
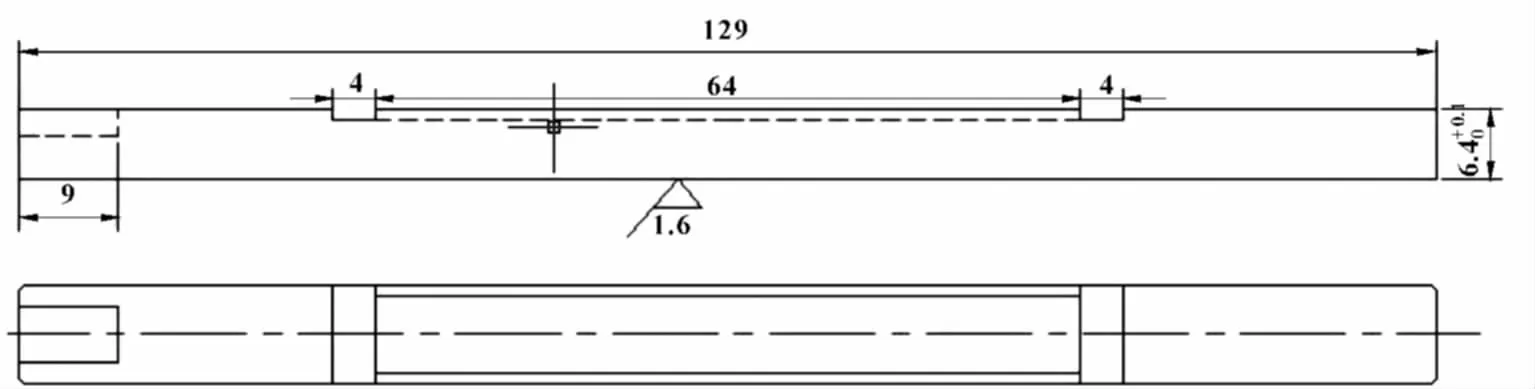
图5 油石座结构

表2 挠性杆-油石座振动实验结果(油石座高度为6.4 mm)
3 结论
由表2 可以看出,由式(18)所计算出来的挠性杆-油石座振动系统的谐振频率,在19 ~23 KHz范围内较为精确。
【1】隈部淳一郎.精密加工——振动切削基础和应用〔中译本〕[M].北京:机械工业出版社,1979.
【2】马大猷.声学手册[M].北京:科学出版社,1983.
【3】赵波,赵勇.超声珩磨装置关键工艺研究[J].机械工艺师,1998(7):11-13.
【4】倪振华.振动力学[M].西安:西安交通大学出版社,1986:359-366.
【5】祝锡晶,王爱玲,辛志杰,等.功率超声珩磨缸套加工中谐振系统的试验研究[J].中国机械工程,2005(5):727-730.
【6】吴秀玲,袁艺.超声珩磨声振系统设计方法初探[J].华北工学院学报,1998(2):168-170.
【7】苏金明,阮沈勇.MATLAB[M].北京:电子工业出版社,2005:191-192.
【8】张云电,喻家英.珩磨负载对超声珩磨振动系统谐振频率的影响[J].声学学报,1994(9):367-371.
