火电厂凝结水处理系统实时样水温度模糊控制
2013-03-14尹龙洁
尹龙洁
(华电能源股份公司哈尔滨第三发电厂,哈尔滨150024)
1 凝结水处理系统混床样水采样分析
在凝结水处理过程中,每隔一定周期都要对混床内的混合样水进行采样进行再分析,以确定水中的离子浓度程度。在采样之前,先升高采样罐的压力使其压力与混床内的压力接近,然后打开采样阀门收集样水进入采样罐,采样罐的水再进入检测容器进行检测。根据检测结果来改变混床内树脂与水的浓度的加入比例。检测过程流程如图1所示。

图1 样水检测流程
经对火电厂凝结水处理系统长期检测,得到了凝结水中含有的常见各种的离子和测量时的合适温度,具体参数如表1所示。
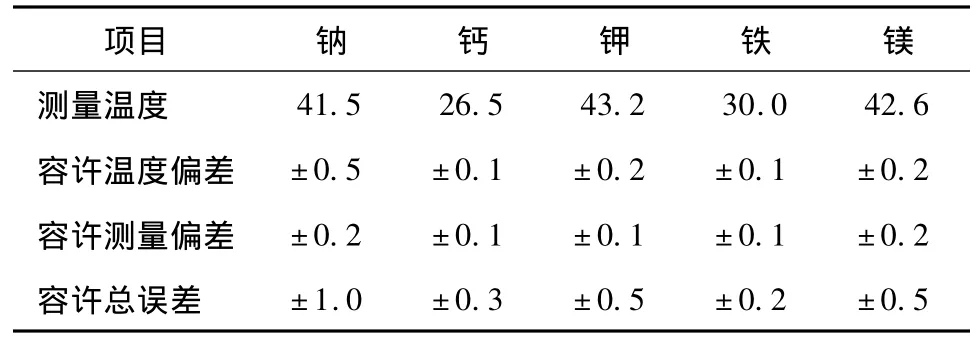
表1 离子参数表 ℃
2 凝结水实时样水温度模糊控制
实时样水温度控制过程通常具有大滞后、时滞或时变、变量强耦合等特点,难以建立精确的数学模型,采用经典控制理论与现代控制理论进行系统的分析和设计比较困难,甚至根本无法获得比较理想的运行效果。因此,提出可采用一种模糊控制,其优点是不依赖于被控对象精确的数学模型,将人的控制经验进行总结,借助于模糊数学工具,利用模糊推理就可以实现对非线性对象比较满意的控制效果,可有效解决此难题[1]。
本文采用二维模糊控制器,以检测温度值Vf与期望值Vr的误差e及其变化率Δe作为输入,以控制器PWM输出信号作为输出。对实时样水温度进行采样,获得其精确值,然后与给定值进行比较得到误差信号e、误差变化率Δe,经模糊化处理成为模糊量E、EC。根据模糊推理规则可得模糊控制量U,再对其进行解模糊得到微控制器的PWM寄存器控制量u。模糊控制原理如图2所示。

图2 模糊控制原理
2.1 输入模糊化
误差信号e、误差变化率Δe的实际取值范围称为基本论域。由于对被控对象不可能精确掌握,因此,我们需要估计基本论域的范围,设变量X的实际取值范围为[a,b],e、Δe的模糊论域选择为[-6,6]。根据式(1),将变化区间为[a,b]的变量X变换为区间为[-6,6]之间变量Y,然后将这一连续的变量离散化,将其分为几档,每一档对应一个模糊集,而后进行模糊化处理。
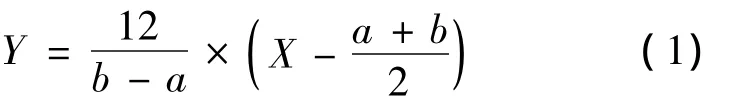
2.2 隶属度函数选取
确定隶属度函数是模糊控制实现的关键,隶属度函数的确定因控制对象和应用环境而异,很多系统都应用经验来选择。
隶属度函数具有反应事物简便性的特点,因此,它应该依据如下准则选取:
原则1:隶属度函数由模糊集合表示,而模糊集合必须为凸模糊集合。即对任意a<x<b,有μx>min(μa,μb)。
原则2:变量所选取的隶属度函数最好为对称的。
实际应用中隶属度函数的选取一般依据模糊分布来确定,常用隶属函数:高斯型、三角形型、梯形。此处采用三角型隶属函数。
e的隶属度函数
温度误差由温度的给定值与温度的检测值之差决定。温度误差值e的论域取{-6,-5,-4, -3,-2,-1,0,1,2,3,4,5,6},在模糊控制区内将温度误差分为7个模糊状态[2]。PB(正大温度误差)、PM(正中温度误差)、PS(正小温度误差)、ZO (零温度误差)、NS(负小温度误差)、NM(负中温度误差)、NB(负大温度误差),即e的语言集:{NB,NM,NS,ZO,PS,PM,PB}。根据所采用的三角形函数隶属度函数对应的模糊状态如图3所示。
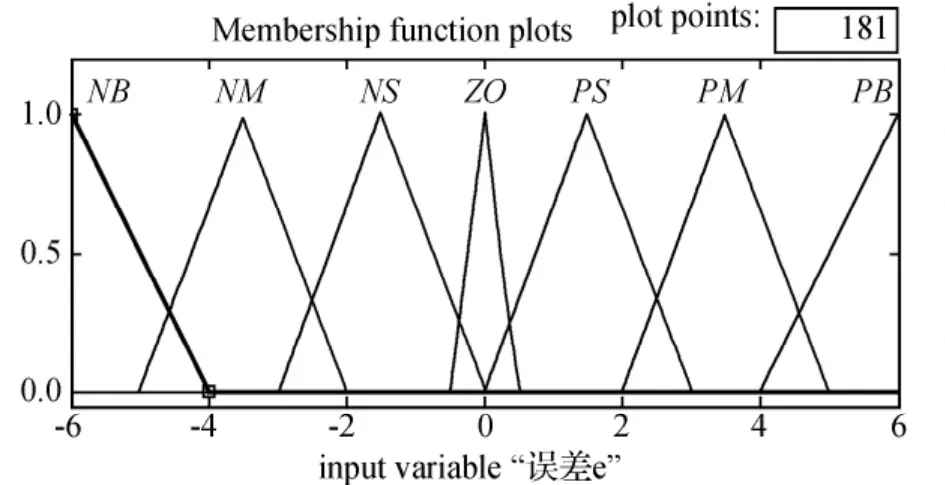
图3 温度误差隶属度函数
Δe的隶属度函数
取温度变化率Δe的论域取{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},即7个模糊状态,Δe的语言集:{NB,NM,NS,ZO,PS,PM,PB}。根据所采用的三角形函数隶属度函数对应的模糊状态如图4所示。
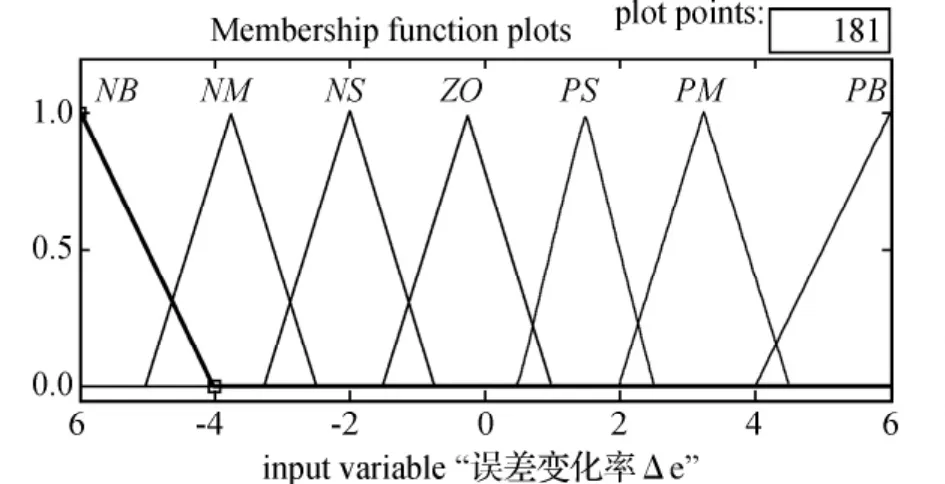
图4 温度误差变化率隶属度函数
触发角变化值Δα的隶属度函数
模糊控制器的输出,即触发角变化值Δα的论域取{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6},对应Δα的语言集:{NB,NM,NS,ZO,PS,PM,PB},其隶属度函数如图5所示。
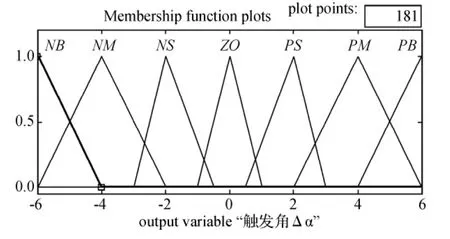
图5 触发角的变化值隶属度函数
2.3 建立模糊控制规则表
模糊控制规则实质上是模糊条件语句的集合,是设计模糊控制器的关键。模糊控制规则的建立一般有3种方法:经验和常识、操作模式、学习。模糊控制规则的型式又分为状态评估和目标评估2种。因状态评估与人的思考一致,多数模糊控制系统都采用这种型式,即:IF E is NB and EC is NB then Δα is PB的一系列模糊控制规则语句。当温度误差较大时,控制量应使误差迅速减少;当温度误差较小时,混床运行期间,实时样水温度模糊控制规则较难于把握。由于样水在混床内时具有一定的压力,因此导致其树脂的吸附度较大。而采集的样水是在常压下,由于压力的改变,原来已经反应的树脂会出现部分还原的现象,因此应在控制规则表中给予考虑,温度误差E的模糊规则如表2所示。
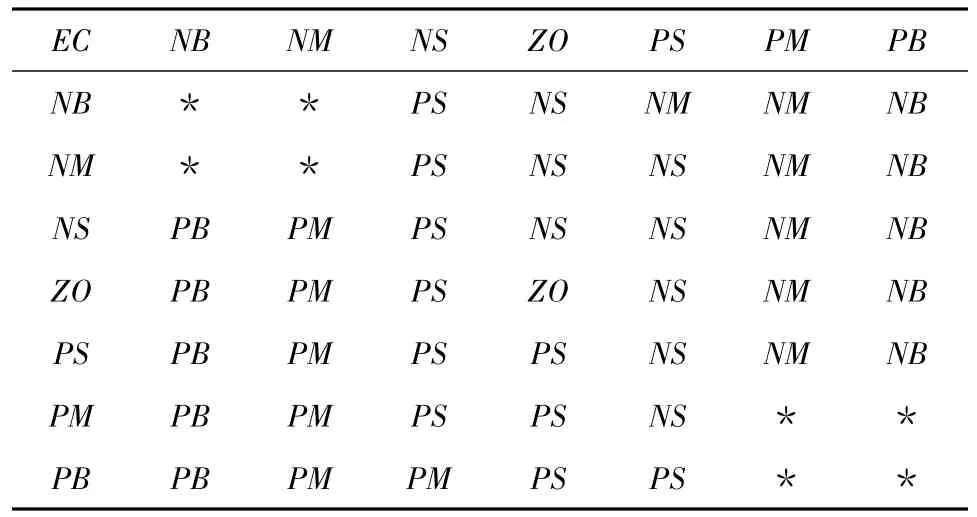
表2 温度误差E的模糊规则
2.4 模糊推理
在模糊规则表建立以后,就可以进行模糊推理。模糊推理是模糊关系与模糊集合之间的合成运算法则,由条件聚合、推理、累加3部分组成。条件聚合是指模糊推理过程中的规则被满足程度,然后依据规则推理,确定单一输出,即推理。最后将所有规则的单一输出,进行合成运算,得到最终的模糊输出[3]。
本系统假设有两条规则:
规则1:若温度误差E为NM且温度误差变化率EC为ZO,则PWM输出口Δα为NM(IF E is NM and EC is ZO then Δα is NM)。
规则2:若温度误差E为NM且温度误差变化率EC为PS,则PWM输出口Δα为NS(IF E is NM and EC is PS then Δα is NS)。
在合成推理中,采用Mamdani推理法中极大极小运算方法作为合成运算法则,该方法是控制系统中最常用的方法,其推理过程如图6所示。
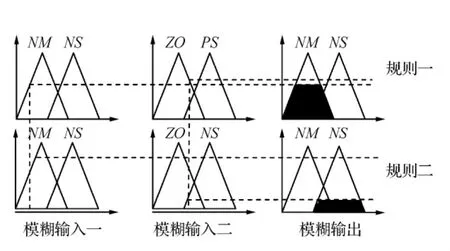
图6 模糊推理过程
控制规则统一格式为:IF E is Aiand EC is Bjthen Δα is Cij。其中,E为温度误差,Ai为对应的语言变量值,EC为温度误差变化率,Bj为对应的语言变量值,Δα为PWM输出口增量,Cij为相应的语言变量值,i、j分别为温度误差和温度误差变化率的模糊语言标号。对应单个规则的模糊关系为
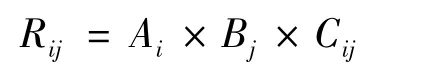
式中:×为内积。
相应的隶属度函数为
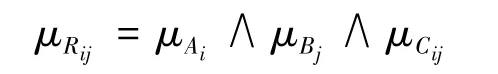
把单一规则合成得到最终模糊关系矩阵为
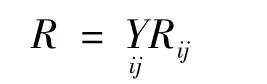
相应的隶属函数为
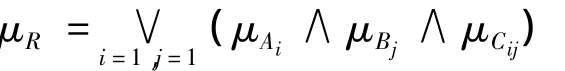
根据模糊关系矩阵,对于测得的模糊量温度误差E和温度误差变化率EC,可得到PWM输出口增量Δα的模糊量输出为

2.5 解模糊化及建立模糊控制器查询表
经过模糊推理得到Δα的模糊量输出U并不能直接用于控制,必须通过解模糊过程转化为一个执行机构可接受的精确量u[4,5]。解模糊过程种常用的方法有3种:最大平均值法、重心法、面积法。其中最大平均值法会产生状态误差甚至使控制信号振荡,只能应用于性能不高的模糊控制系统中,而重心法具有较好的逻辑性和严谨性而在模糊控制中广泛应用,其计算公式为
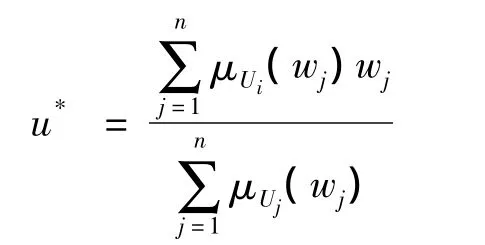
式中:Ui为各输出量模糊子集;μUi(wj)为其隶属度函数质心;wj为和隶属度值;u*为精确控制量。
在模糊控制过程中,给出特定的输入,一般经过检测得到,经模糊化、模糊推理、解模糊,即可得到执行装置的精确控制量。在实际应用中,根据经验预先确定好输入量的取值区间,对区间合理规划后离散化;根据模糊控制过程计算出特定输入所对应的精确控制量输出,建立它们之间的对应关系表,称为模糊控制器查询表。然后依据此表对系统进行快速准确地控制。
3 仿真实验
本文将模糊控制技术和S3C44B0微控制器相结合进行MATLAB仿真实验[6]。S3C44B0处理器的A/D转换接口需要0至2.5 V的电压,每一个离散值对应相应的温度,温度值在10~80℃之间。输入信号采用触发器作为S3C44B0的输入信号,触发器的输入信号的幅度为2.5的正弦波,即触发信号幅度为2.5、频率为1的方波。图7为触发器模型图,图8为触发器的输出波形,即微控制器的A/D输入信号。

图7 触发器模型图
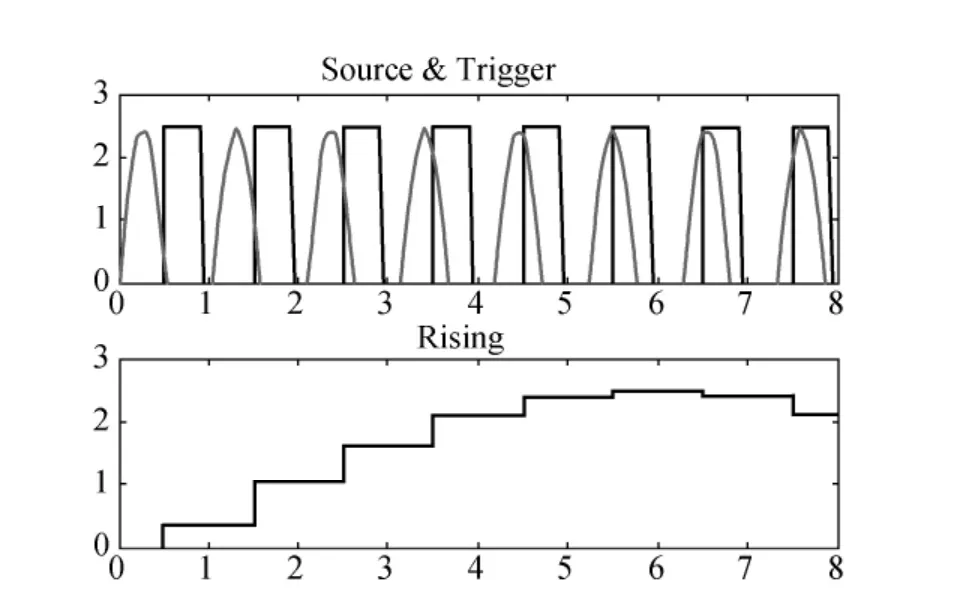
图8 A/D输入信号
温度控制系统近似为惯性环节和纯滞后环节的合成,其传递函数为

为了便于进行仿真,取T1=1,T2=1,T3=0.2,K=0.2,σ=1,通过Simulink中的基本库和模糊逻辑工具箱模块,模糊控制系统仿真如图9所示。
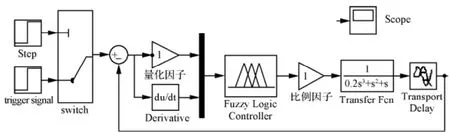
图9 模糊控制系统仿真

图10 模糊控制系统阶跃响应
当开关在“step”时,其响应曲线如图10所示。从图10中可以看出,在阶跃信号的输入下,模糊算法控制把超调量控制在10%以内,没有振荡现象,提高了系统的稳定性。
4 结语
分析了火电厂凝结水处理系统,了解了该系统关键部分是对混床内实时样水中的离子成分进行检测,并决策出实时加入的树脂量。介绍了基于嵌入式系统并采用模糊控制技术成功应用在火电厂凝结水处理系统的实时样水温度检测过程。实现了非线性控制的任务,避免了由于混床内与混床内各环境参数不同而引起样水温的误差从而影响水处理精度这一基本问题。仿真实验验证了该控制器运行稳定、可靠、适应性强。
[1] 廉小亲.模糊控制技术[M].北京:中国电力出版社,2003. 324-407.
[2] ZADEH LA,Fuzzys.Informat Control[J],1965,22(8):338-353.
[3] CHING-CHANG W,LIN Nine-shen.Rule extraction for Fuzzy Modling[J].Fuzzy Sets and Systems,1997,88(1):23-30.
[4] JANARDHANA I S,Sastry V V[Z].Fuzzy Logic Based Softstart for Induction Motor Drives.Fuzzy Logic,1995.
[5] MIR S A,ZINGER D S,ELBULUK M.Fuzzy controller for inverter fed induction machines[Z].Fuzzy Controller Design,1994.
[6] 黄勋刚,黄华高,季国瑜.基于MATLAB的自动控制过程的仿真[J].计算机仿真,2003,20(7):101-104.
