变压器油箱涡流损耗的三维有限元分析

2013-03-14宫丽娜刘文里吴明君

黑龙江电力 2013年2期

宫丽娜，刘文里，吴明君，叶俭

(哈尔滨理工大学电气与电子工程学院，哈尔滨150080)

大容量变压器的杂散损耗有时可以达到负载损耗的30% ～40%，因此杂散损耗是不可忽视的［1］。在产生的杂散损耗中，金属结构件中的漏磁分布及涡流分布极不均匀，容易产生局部位置损耗集中而引起过热现象，尤其油箱中的涡流损耗在结构件中所占比例较大而且分布不均匀，因此掌握油箱中漏磁分布及减小其中的涡流损耗是非常重要的［2］。

由于变压器漏磁分布的不规律性及金属结构件形状的不规则性，在变压器厂进行工程计算时，通常不能单独给出各个金属结构件的涡流损耗，而是整体作为附加损耗的一部分进行估算。为了解各金属结构件漏磁分布情况及具体涡流损耗分布及数值大小，本文采用ANSYS有限元软件对大型变压器箱体三维漏磁场及涡流场进行了分析计算，并对减小损耗的关键因素详细分析。

1 计算难点及模型简化处理

1.1 油箱漏磁计算难点

变压器油箱属于铁磁材料，当其处于正弦变化的漏磁场中，由于集肤效应的影响，磁通绝大多数聚集在导体表面，所以磁场强度会从油箱表面沿垂直方向向内部逐渐呈指数衰减，衰减至零时所到达的深度即为透入深度［3］。箱体的透入深度可按下式计算:

式中:d为透入深度;ω为正弦变化的角频率，工频时ω=2πf=314;μ为材料的磁导率，μ=μ0μr= 4π×10-7×200=2.512×10-4H/m;γ为材料的电导率，γ=7.6923×106s/m。由此可知变压器油箱的透入深度为1.8 mm，小于它的厚度。

1.2 模型简化处理

以1台220 kV/180 000 kVA三相五柱式电力变压器为例进行计算，由于其尺寸较大，考虑计算机容量以及更好划分网格以提高计算速度及准确性，做出如下假设:

1)近似认为变压器箱壁的材料均匀、线性、各向同性。

2)变压器结构关于绕组中心连线纵向轴面前后对称。

3)各相绕组的总安匝数为零，绕组内的电流密度分布均匀［4］。

4)场域中的场量随时间作正弦变化，忽略高次谐波。

5)忽略位移电流的影响。

6)箱盖与箱壁、箱底与箱壁均为直角连接，忽略绕组各相间的相互影响。

2 建模计算

2.1 ANSYS软件电磁分析原理简介

本文研究的主要内容是在工频下工作的，时变电磁场的变化频率很低，属于似稳电磁场问题。在库仑条件▽·A=0的规范下，似稳电磁场的方程为

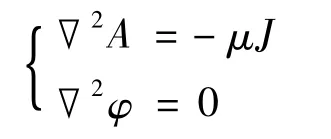
式中:A为矢量磁位;φ为标量电位;J为电流密度(A/mm2);μ为磁导率(H/m)。

变压器金属结构件涡流损耗的计算是以漏磁场分析为基础的。由前面计算漏磁场求得的矢量磁位A和标量电位φ可求出涡流密度Je的分布。由涡流密度可求得单位体积的涡流损耗密度We为

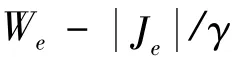
金属结构件表面的涡流损耗Ws为

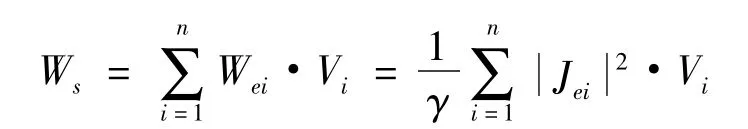
金属结构件的涡流损耗W为

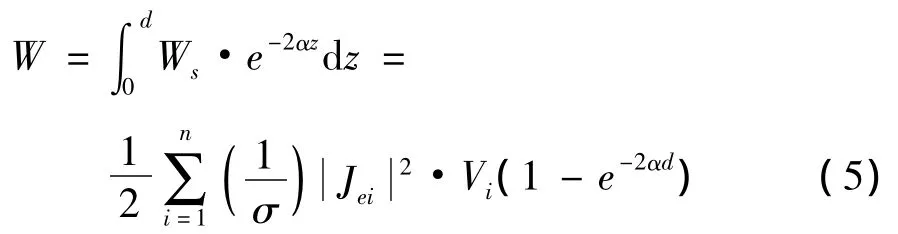
式中:n为积分点个数;Ws为积分单元i的涡流损耗密度;Jei为积分单元i的电流密度;σ为材料的电导率;Vi为积分单元i的体积;d为材料厚度;α为电磁波衰减系数，是透入深度的倒数［5］。

2.2 计算过程

1)建模。为了更真实地反映变压器实际漏磁场的分布情况，在建模时将变压器主要部件全部包括，模型如图1所示。

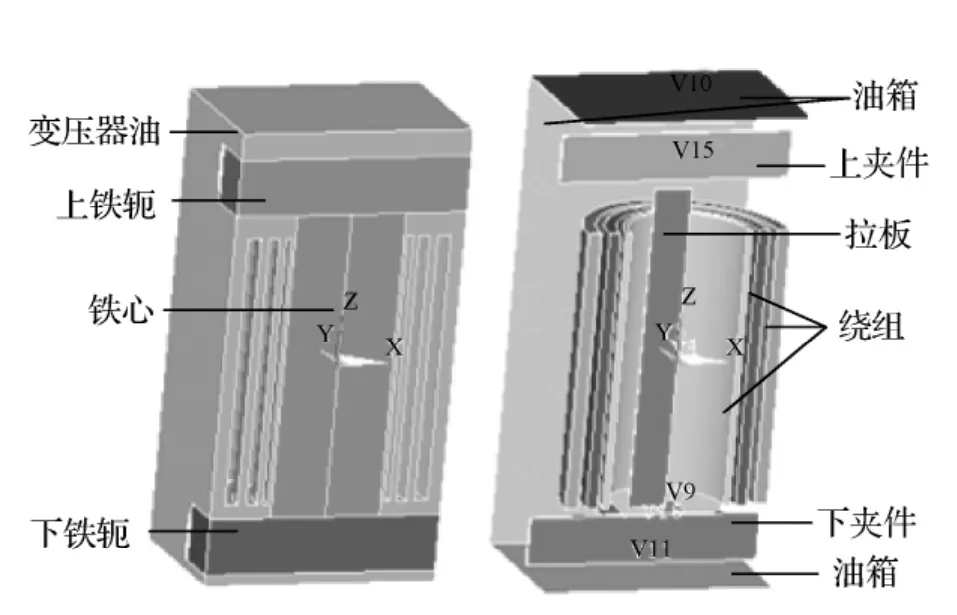
图1 变压器漏磁场计算模型

2)定义单元类型及材料属性。采用棱边单元法，材料属性如表1所示，均按变压器实际参数定义，单元类型solid117。绕组、铁心、变压器油、空气的自由度为AZ，其余为AZ和VOLT。

表1 变压器材料属性表

3)剖分。变压器油和铁心铁轭均采用自由剖分，油箱、夹件、拉板、绕组采用扫略剖分。值得注意的是，考虑油箱壁透入深度因素，厚度方向必须进行多层剖分。剖分时尽量保证整体单元大小近似且油箱为计算对象一定要尽量细剖。

4)边界条件及激励。棱边单元法需设定平行边界条件，垂直边界条件默认，无需定义，外边界若不定义均按垂直处理。对油箱外侧及对称面施加平行边界条件，其余均为垂直。激励的选择是对绕组施加电流密度，电流密度按磁势平衡条件施加。

5)求解。选择谐波分析方法及Sparse求解器检查载荷步即可以计算，后处理中读取结果。

补充一点，由于计算过程需要多次改动模型尺寸、材料等条件，如果直接按菜单操作十分繁琐，所以在整个计算过程中均采用命令流方式。

3 屏蔽前变压器油箱漏磁场与涡流损耗分析

按2.2节计算过程计算后，变压器箱壁漏磁场云如图2所示。

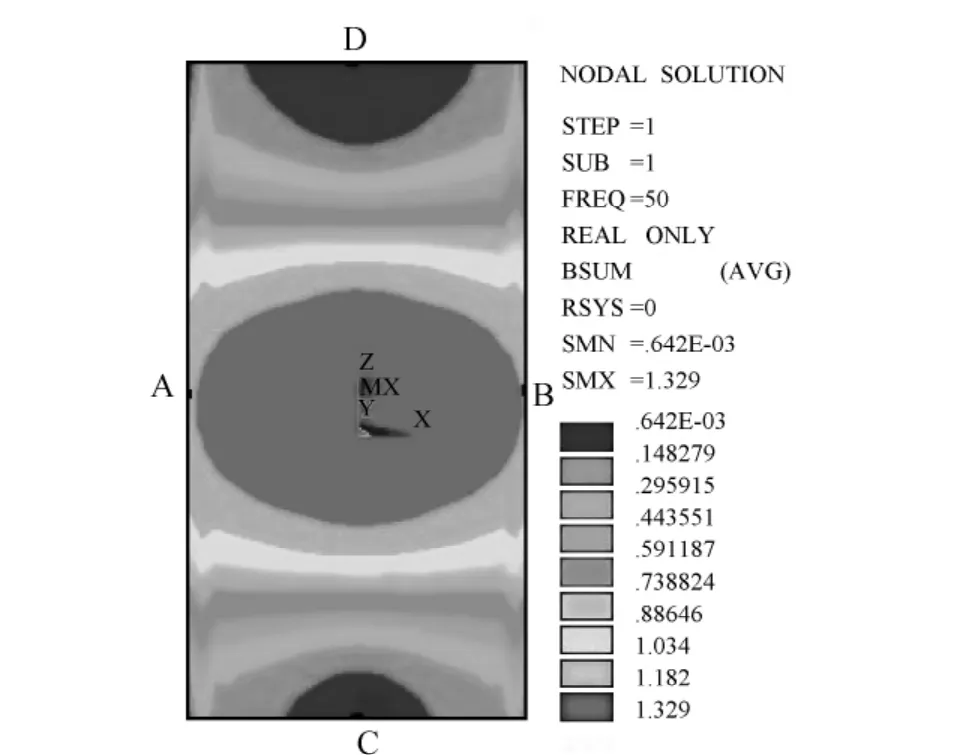
图2 油箱中漏磁场分布

由图2可以看到，从油箱后壁整体来看，箱壁中部与绕组外径最近处漏磁密度最大，然后沿着箱壁高度和宽度方向向两侧逐渐降低。这是由于箱壁中部离绕组最近，漏磁通最大，闭合的磁力线最多。图3—图11是在相应仿真计算后在软件中读取的结果。

图3 油箱壁内表面沿AB总漏磁分布图

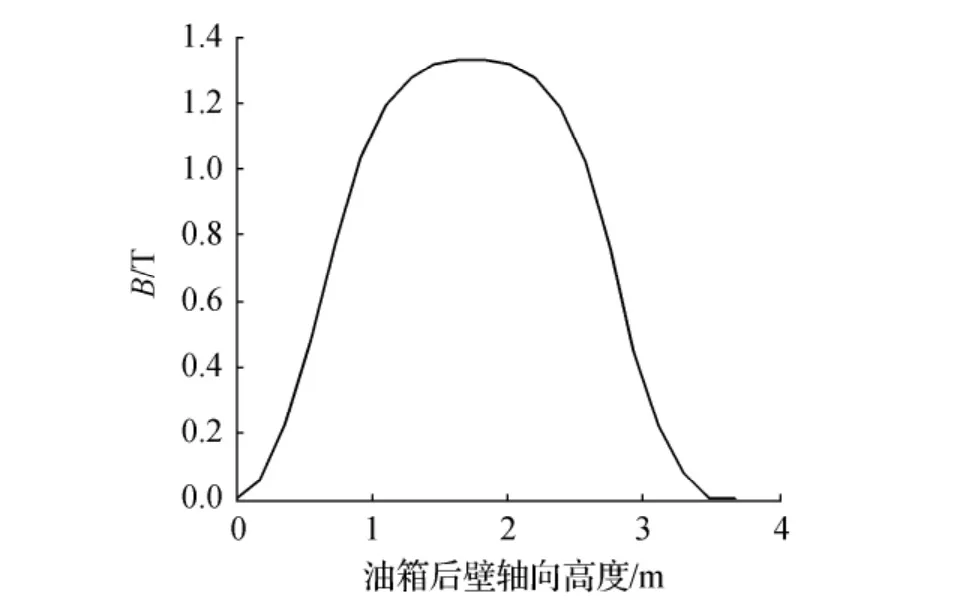
图4 油箱壁内表面沿CD总漏磁分布图

由图3、图4的曲线可以进一步看到磁密沿高度、宽度方向的变化，并且可以看到沿宽度变化幅度相对高度方向小很多。这是因为高度方向跨度大，距离绕组较远，到达的磁力线越来越少，至油箱顶部几乎为零。由图5、图6可以看出，与绕组端部对应的油箱区域漏磁密度的辐向分量最大，与绕组中部对应的油箱中部区域漏磁密度的轴向分量最大。这是因为磁力线流经绕组到达端部时产生弯曲，垂直或倾斜进入油箱产生辐向的漏磁分量，然后经过油箱而闭合。离绕组越近的油箱中部，其中闭合的漏磁通最多，有些磁力线没有到达绕组端部直接与油箱形成闭合回路，所以油箱中部离绕组最近处磁密最大。

图5 油箱壁内表面法向漏磁分布

图6 油箱壁内表面切向漏磁分布

从图7可以看出涡流损耗密度在箱壁中部最大，其变化规律与其漏磁分布类似，这是因为磁密大的部位感应出的涡流密度也大，涡流密度大的区域涡流损耗密度随之也大，进而损耗也大。根据这一点可以通过减小箱壁漏磁集中部位的幅值以及改善箱壁漏磁分布来减小箱壁损耗及降低最大涡流密度。这样既可以减小整体损耗，又可以削弱涡流密度最大值，防止局部过热。

4 采用磁屏蔽后油箱的涡流损耗

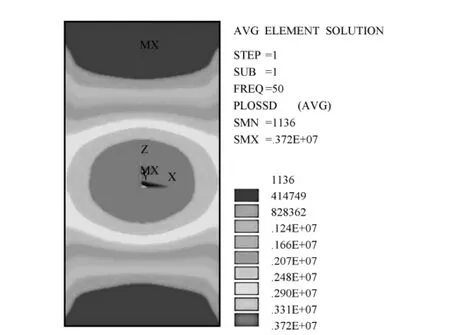
图7 油箱涡流损耗密度分布图

为减小油箱涡流损耗，在距离油箱后壁内侧3 mm处安放磁屏蔽。油箱磁屏蔽是用硅钢片制成的，由于磁屏蔽在油箱内表面，磁导率比较高，原来进入油箱的磁通这时进入到磁屏蔽中，此时油箱中的漏磁密度降低，进而涡流损耗也大大降低［6］。一般变压器用硅钢片相对磁导率为2 000，是文中箱壁的10倍，从绕组出来的磁力线会被磁屏蔽所分流，从而使大部分磁通从屏蔽中流过，使得进入箱壁磁通大大减小，降低了其中的磁密，减小了损耗。采用磁屏蔽后的漏磁和涡流损耗密度如图8、图9所示。

图8 屏蔽后油箱壁漏磁场分布图

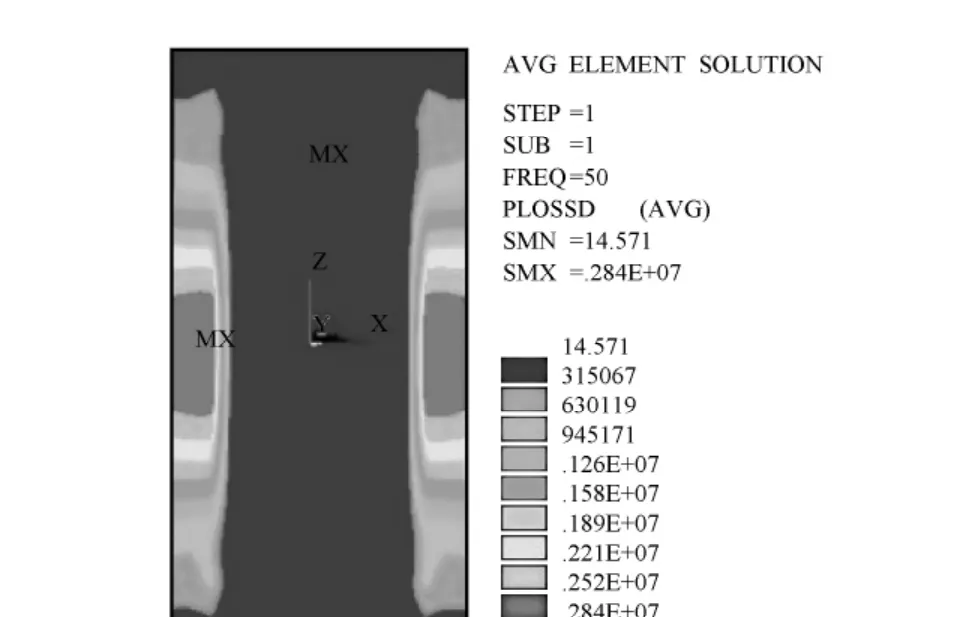
图9 屏蔽后油箱壁涡流损耗密度分布图

从图10、图11中可以看出油箱被屏蔽区域磁密的最大值由屏蔽前的1.329 T降低至0.04347 T。对比图7、图9可以看到油箱被屏蔽区域的最大涡流损耗密度由3 720 kW/m3降至315.067 kW/m3以下，整体涡流损耗密度最大值由3 720 kW/m3降至2 840 kW/m3。此外可以清楚地看到屏蔽遮挡的箱壁区域磁密已降至很小，未遮挡区域磁密也有所下降。可见采用磁屏蔽后既降低了漏磁密度幅值，又改善了漏磁分布，大大降低涡流损耗密度，改善了涡流分布，进而降低了箱壁的损耗。

图10 屏蔽后油箱壁内表面沿CD总漏磁分布图

图11 屏蔽后油箱壁内表面沿AB总漏磁分布图

表2—表4分别是以屏蔽宽度为1.224 m、高度为2.89 m、厚度为0.03 m为基准，各物理量最大值随屏蔽不同宽度、高度和厚度变化的对比表，表中涡流损耗值和经验公式计算值基本相符。

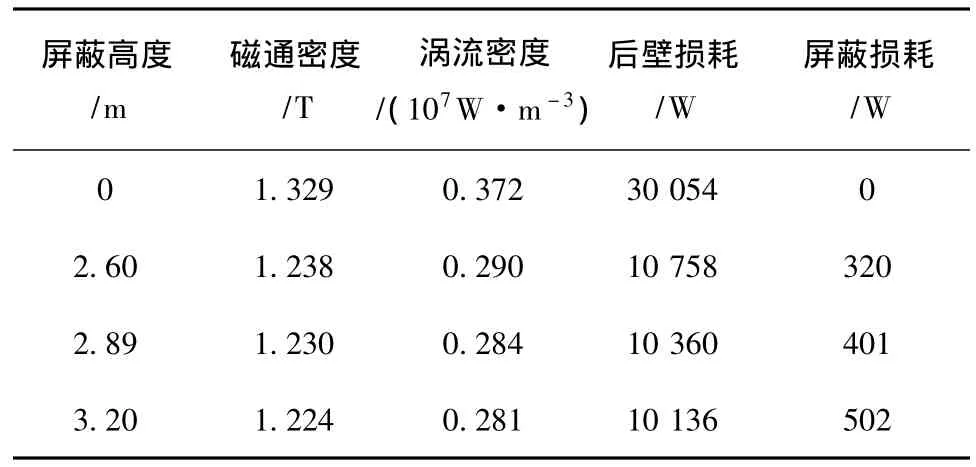
表2 屏蔽高度变化时各值的比较

表3 屏蔽厚度变化时各值的比较

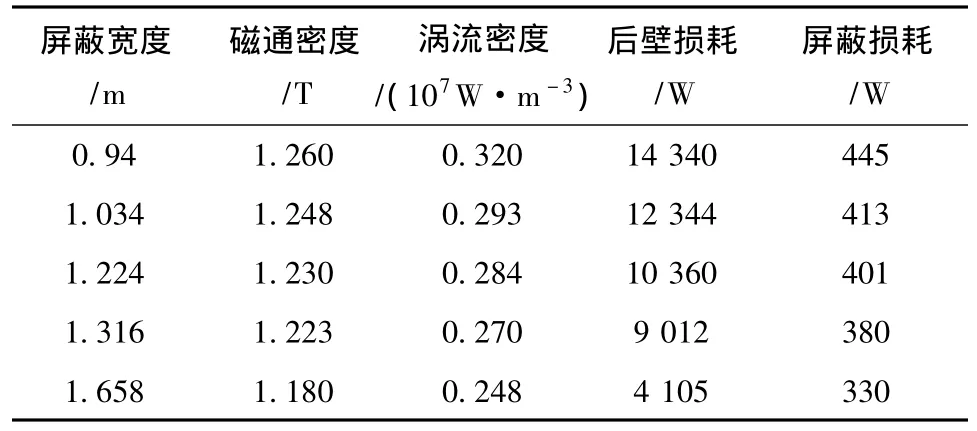
表4 屏蔽宽度变化时各值的比较

从表2—表4可以看出，无论是增加屏蔽的高度、宽度还是厚度，油箱中的损耗都随之降低。这是因为随着磁屏蔽厚度的增加，屏蔽的磁阻随厚度的增加而减小，分流效果就愈好，因此屏蔽效果就越好;结合图2、图3可以看出，漏磁沿油箱宽度方向两侧与中间幅值变化幅度小，因此增加屏蔽宽度可以迅速减小箱壁漏磁较大的区域，损耗随之下降的愈明显;结合图4可以看到，漏磁沿油箱高度方向从中间向两边幅值下降很大，因此增加屏蔽高度油箱损耗也是随之下降。但是超过屏蔽2.89 m(高度约在铁轭中间)，再继续增加屏蔽高度损耗下降幅度变小。综合来看增加屏蔽尺寸对减小油箱损耗是有利的，但是结合经济性以及某些因素(如高度)，超过一定范围减小幅度变小，屏蔽尺寸并非越大越好，而是使油箱损耗降低到要求范围内即可。

由此模型折算到整个油箱的损64.567 kW，工程算法杂散损耗为