超高速目标及其绕流场雷达散射模拟与分析

于哲峰 梁世昌 部绍清 石安华 马 平 黄 洁 刘佳琪

（1.中国空气动力研究与发展中心，四川 绵阳621000；2.试验物理与计算数学国家级重点实验室，北京100076）

引 言

超高速目标再入大气层或在临近空间飞行时，目标与空气发生强烈的相互作用，目标周围的空气被急剧压缩，形成发光、电离的高温气体.由于高温气体的作用，目标材料将被加热甚至出现热解、烧蚀.同时，由于高温空气和目标材料烧蚀产物的电离，在目标表面形成等离子鞘套，在其下游形成电离尾迹，严重影响再入段目标电磁散射特性.对这些复杂的物理化学过程进行研究，涉及到空气动力学/热力学、电磁学以及光学等诸多领域，研究难度极大.从20世纪60年代开始，美国、前苏联等国投入大量人力物力开展这方面研究［1-8］.在国内，最近几年对这方面的研究也越来越重视，主要研究单位有中国空气动力研究与发展中心、航天科技集团一院、国防科学技术大学、北京航空航天大学等［9-14］.

本文对于超高速目标及其绕流场RCS特性的研究思路为：开展理论分析方法研究，建立基于并行时域有限差分方法的超高速目标及其绕流场电磁散射特性的物理模型、数学模型，编制相应程序.利用中国空气动力研究与发展中心气动物理靶开展地面试验，将地面试验测量结果与仿真结果进行对比，验证仿真方法的有效性.最后，开展给定飞行状态下某再入目标RCS特性仿真研究，分析等离子体绕流对实际飞行状态下再入目标RCS特性的影响.

1 理论分析方法研究

超高速目标及其绕流场是一个典型的多目标耦合散射研究的问题，既包括超高速目标金属本体又包括非均匀等离子体绕流，等离子体绕流每一处介电常数都不同，并且，等离子体为色散介质，其介电常数随入射波频率变化而变化.FDTD方法可以非常灵活地对每一个网格点的介电常数进行设置，对等离子体可以采用特殊的差分格式进行处理，对电大尺寸问题可以利用并行计算进行模拟，非常适合于研究这类复杂问题.

1.1 物理模型

在计算等离子体RCS时，常把等离子体看作是一种电介质.对于非磁化冷等离子体，它的相对介电常数εr是复数，并且有如下形式为

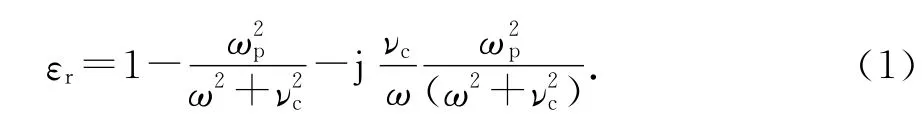
式中：ωp＝［nee2/meε0］1/2为等离子体频率（me是电子质量，e是单个电子所带的电量，ε0是真空介电常数，ne是每立方米的电子数）；ω是入射电磁波的角频率；νc是电子与中性粒子的碰撞频率.

1.2 数学模型

在利用FDTD方法分析等离子体鞘套的雷达散射特性时，需要对等离子体进行特殊处理.本文采用的是直接积分方法［6］.考虑目标的金属表面覆盖着一层非磁化冷等离子体，等离子体中的离子因其质量远远大于电子质量而可忽略其运动，此时Maxwell方程组可以写为

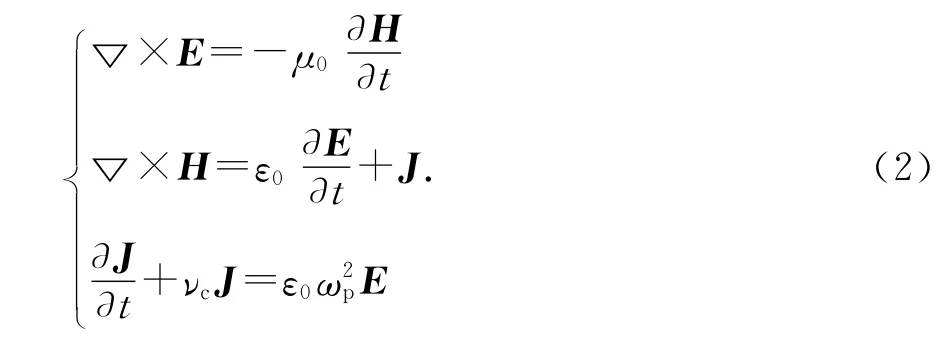
式中：E为电场强度；H为磁场强度；J为电流密度.采用直接积分方法对方程组（2）中第三式进行离散，得到如下方程：

1.3 并行算法

为了加快求解速度，增强电大尺寸问题的模拟，发展了FDTD并行算法.进行FDTD并行算法设计的前提首先是对FDTD计算任务进行空间和时间上的合理分割，以适应不同计算节点加载不同计算任务.并行算法设计还包含其它外围问题处理的设计和流程，这些FDTD外围相关问题包括：计算模型的分割、吸收边界的分割、连接边界的分割、近远场变换积分面的分割及各节点计算任务平衡问题等.

1.4 程序编制

编制了基于并行FDTD方法的超高速目标及其绕流场RCS计算程序.该程序采用Visual Fortran编程，可以计算复杂目标及其绕流单站/双站雷达散射截面.每次计算需给定流场数据以及计算所需的电磁参数条件.经过计算可以分别获得垂直极化与水平极化的复杂目标及其绕流的RCS计算结果.

在模拟时，吸收边界条件采用完全匹配层边界条件，模型网格为Δx＝Δy＝Δz＝δ，δ≤λ/20（其中λ为波长），时间步长Δt＝δ/2c（其中c为真空中波速）.并行计算时服务器可以同时运行8个线程，仿真时对计算区域进行二维拓扑，空间化分为2×4块.

1.5 算法验证

为了验证本文采用的FDTD算法的正确性，计算了等离子体球的双站RCS并与Mie理论得到的解析结果进行了对比.等离子球的双站RCS根据Mie理论可以写为

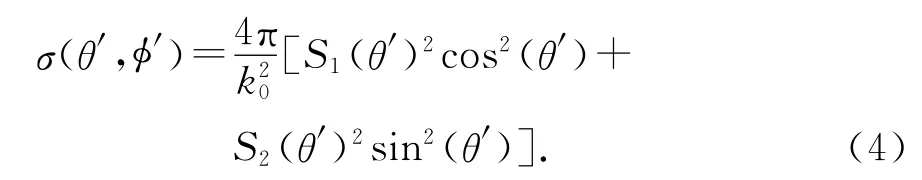
式中：k0为自由空间波数；θ′和φ′的物理意义、S1（θ′）和S2（θ′）的表达式见文献［7］.

进行对比时，假设入射波频率f＝1.0GHz，等离子体球的半径r＝0.2m，等离子体频率ωp＝3.0 GHz，电子碰撞频率νc＝1.0GHz.H 平面和E 平面对比结果如图1所示，由图1可看见，由直接积分法所得到的结果与Mie理论得到的结果符合得较好.另外，对比了其它频率上（2GHz和3GHz）FDTD方法的计算结果与Mie理论的计算结果，发现不同频率上FDTD方法与Mie理论计算结果略有差别，但是都不大于1dB.这说明了本文采用的计算等离子体电磁散射特性程序的正确性.

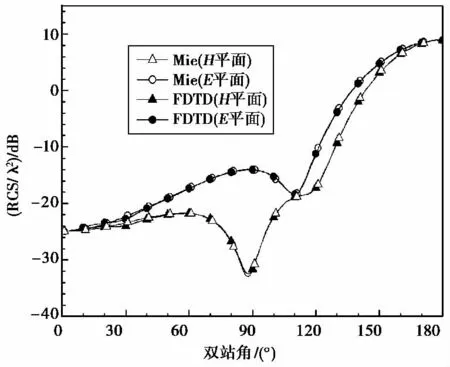
图1 等离子体球的双站RCS

2 典型试验和结果对比

为了研究超高速目标及其绕流场RCS特性，在中国空气动力研究与发展中心气动物理靶上开展了相关试验研究，获得了气动物理靶模型及其绕流场X波段和Ka波段单/双站RCS.

2.1 超高速模型及其绕流场RCS试验

试验时，利用发射器口径为φ＝25mm的二级轻气炮将模型发射到试验要求的飞行速度.在试验段，靶室/真空系统提供模型飞行压力环境，模拟飞行高度.目标飞过雷达波束区时，获得相应测量方式下目标的RCS数据.

在试验中，采用如图2所示的坐标系来说明雷达的布置情况，其中θ为入射波和z轴的夹角，φ为入射波在x-y平面投影和x轴的夹角.

图2 坐标系示意图

两部多普勒雷达的工作频段分别为X波段和Ka波段，可以测量运动目标的单/双站RCS.单站测量时入射波波矢方向为θ＝45°，φ＝90°，反射波波矢方向为θ＝135°，φ＝-90°.双站测量时入射波波矢所在方向为θ＝0°，φ＝90°，反射波波矢所在方向为θ＝113°，φ＝-90°.

图3给出气动物理靶模型、绕流场和尾迹RCS一维距离像的典型测量结果，试验时模型的头部半径为1mm，底部直径为15mm，半锥角为7.9°.靶室压力为2.2kPa，飞行速度为4.4km/s.图中加权平均和极大值为对原始雷达数据处理的两种方法.加权平均意义为大于幅值门限的信号认为是同一个目标，进行速度估计，得出相应位置上的尾迹像.极大值意义为由极大值获得速度分布指标，利用指数拟合速度，得出相应位置上的尾迹像.

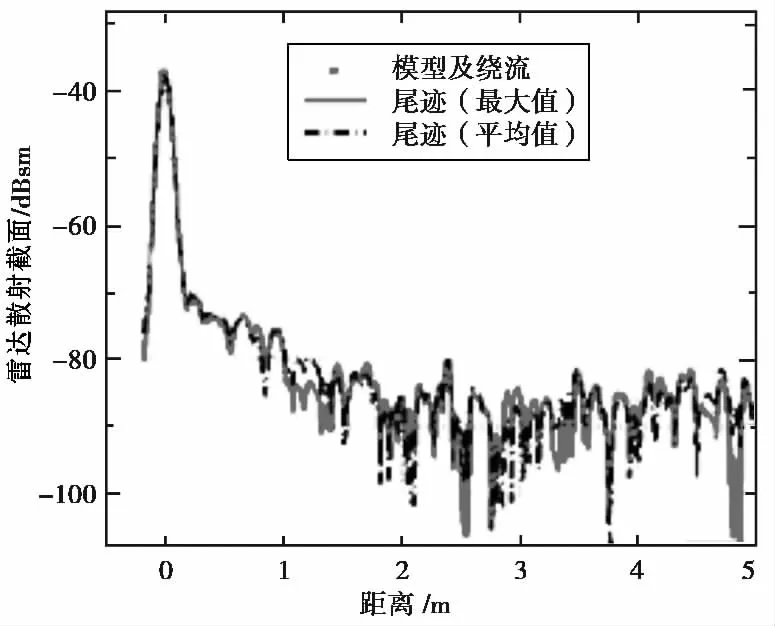
图3 模型RCS一维距离像

2.2 仿真与试验结果对比分析

针对气动物理靶试验，开展了仿真研究，主要步骤包括：首先，要确定飞行模型周围绕流的空气动力学特性；其次，要根据绕流场的空气动力学特性确定等离子体绕流场的电子密度和碰撞频率；然后，给出绕流场的介电常数；最后，通过求解Maxwell方程来给出超高速目标及其绕流的雷达散射截面.

流场数据由中国空气动力研究与发展中心的高铁锁研究员和董维中研究员提供.图4是当大气压力为2.2kPa，飞行速度为4.4km/s，攻角和侧滑角为0°时，气动物理靶模型周围流场的等离子体电子密度分布截面图.

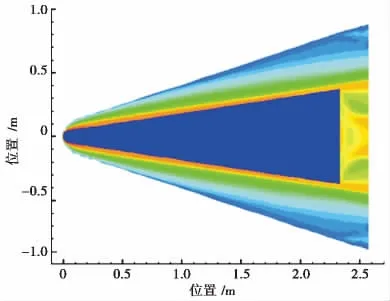
图4 等离子体中电子数密度分布截面图

从图4可以看出，等离子体电子密度ne沿着锥体对称轴（y轴）对称分布，最大值（在钝锥头部）达2.8×1013cm-3，从而可知ωp的最大值可达2.98×1011rad/s.从电子密度分布还可以看出，在钝锥的侧面，贴近目标附近的电子密度较高，远离目标的电子密度较低，对电磁波散射有影响作用的主要是贴近目标的等离子体层.

电子和中性粒子之间的碰撞频率是电子碰撞频率的主要部分，影响等离子体的介电常数和电导率，因而与电磁波的传播、吸收和散射特性密切相关，是决定等离子体电磁散射特性的重要参数之一.本文采用文献［8］给出的有效电子碰撞频率计算公式为

式中，T为等离子体温度.

气动物理靶模型及其绕流场的RCS仿真和试验结果对比如表1所示.从对比结果可以看出：当飞行速度为4.4km/s，压力为2.2kPa时，X波段单/双站RCS数值模拟结果和试验测量结果之间差值分别为2.5dBsm 和0.4dBsm，Ka波段单/双站RCS数值模拟结果和试验测量结果之间差值分别为1.9dBsm和2.4dBsm，四种状态下最大差值为2.5dBsm.

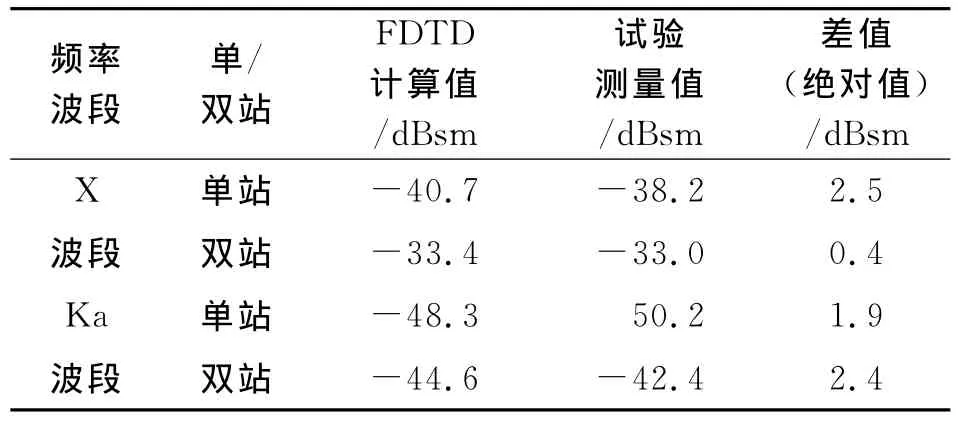
表1 数值模拟结果和试验测量结果对比表

为了寻找仿真结果和试验测量结果之间存在差值的原因，利用并行FDTD程序，分析了雷达入射角小角度偏离对模型及其绕流场RCS的影响规律.下面简要地进行介绍：

在气动物理靶试验中，模型飞过雷达测量段时总是带有一定的攻角和侧滑角，而在仿真时假设模型飞行时攻角和侧滑角为零，因而存在一定的偏差.需要考虑雷达入射角小角度偏离对气动物理靶模型RCS的影响.为此，分析了压力P＝2.2kPa，速度V＝4.4km/s时，雷达入射角小角度偏离对模型X波段单站RCS的影响.

计算时，偏离角δ＝-3°～＋3°，也就是入射波所在的平面为θ＝42°～48°，φ＝90°，计算结果如图5所示.从图5可以看出，随着雷达入射角的偏离，模型RCS的仿真值也出现了变化.当θ分别为42°，45°和48°时，RCS分别为-38.1dBsm，-40.7dB-sm和-42.9dBsm.θ分别为42°和48°时 RCS与θ为45°时的RCS最大差值为2.6dBsm.由此可见雷达入射角小角度偏离对模型及其绕流场RCS影响很大，在后续开展的研究中要增加攻角和侧滑角的观测以增强分析的准确性.

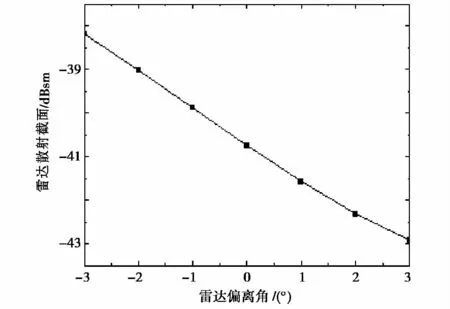
图5 雷达入射偏离角度对模型X波段RCS的影响

3 再入钝锥及其绕流场的RCS

在仿真方法和地面试验研究的基础上，开展了给定飞行状态下某再入目标RCS特性仿真研究，分析了等离子体绕流对实际飞行状态下再入目标RCS特性的影响.

某钝锥体底部直径为750mm，半锥角7.9°飞行高度为H＝50km，速度马赫数为Ma＝15.根据相应飞行条件下的绕流场数据，计算了带绕流场的钝锥RCS.

入射波均从钝锥头部沿锥轴方向入射，当电尺寸k0a＝0.88、3.81和8.79时的双站 RCS分别如图6、图7和图8所示，其中a为模型特征尺寸.可以看到，当k0a＝0.88，绕流场对双站角不是很大时的RCS缩减较大；当k0a＝3.81时，绕流场对双站角很小时的RCS缩减较大，入射角比较大时钝锥单站RCS在无等离子体时值的附近震荡；而当入射波频率为k0a＝8.79时，在所有角度下，钝锥单站RCS在无等离子体时值的附近震荡.

当k0a＝3.81，入射波从各个角度入射时单站RCS如图9所示.从图9可以看出，在不同入射角度下，绕流场对钝锥RCS的作用出现不同情况.当入射波沿着锥轴方向附近入射时，绕流场对钝锥单站RCS有较强的衰减；在入射角比较大的情况下，钝锥单站RCS在无等离子体时值的附近震荡.入射波沿着锥轴方向附近入射时RCS衰减比较大可以解释为：当入射波沿着锥轴方向附近入射时，钝锥体的主要散射中心为锥底，而入射波入射到锥底并反射回来经过了较长的等离子体区域，能量大幅度衰减，因而此时单站RCS衰减比较大.

图6 钝锥及其绕流场k0a＝0.88时的双站RCS

图7 钝锥及其绕流场k0a＝3.81时的双站RCS

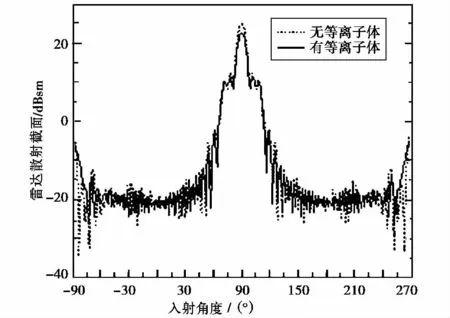
图8 钝锥及其绕流场k0a＝8.79时的双站RCS

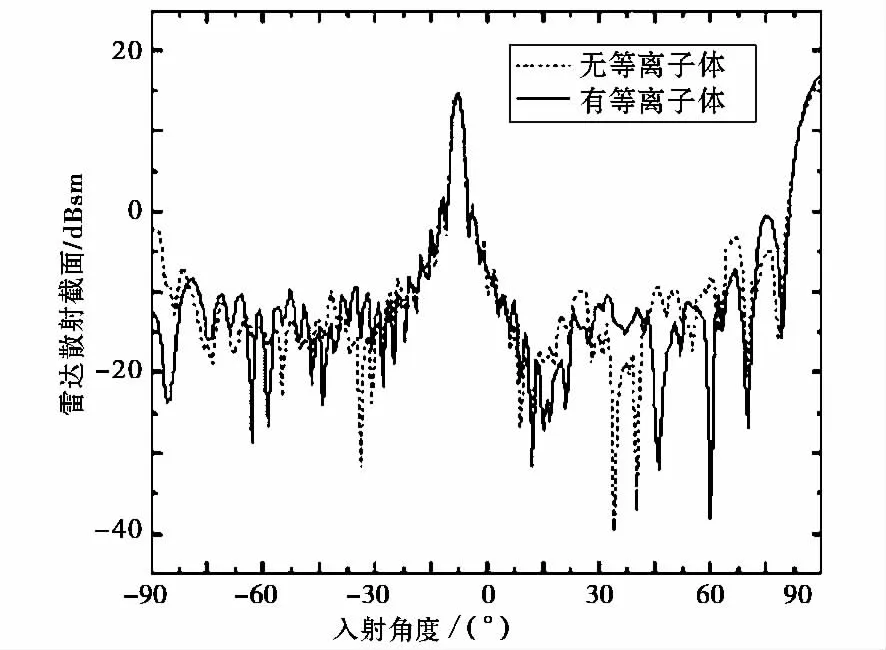
图9 钝锥及其绕流场k0a＝3.81时的单站RCS

4 结 论

采用并行时域有限差分方法计算和分析了气动物理靶超高速模型及其绕流场的RCS，将计算结果和试验测量结果进行了对比.由分析结果可知：数值模拟结果和气动物理靶试验测量结果基本一致.雷达入射角小角度偏离对RCS会产生明显影响，当模型飞行速度为4.4km/s，压力为2.2kPa时，如果雷达入射角小角度偏离±3°，模型及其绕流场X波段单站RCS最大变化为2.6dBsm.

本文还模拟了给定飞行状态下绕流场对钝锥RCS的影响，分析结果显示：绕流场对钝锥RCS的影响与入射波频率、角度以及雷达制式等有关.当入射波从钝锥头部沿着锥轴方向附近入射时，由于入射波入射到锥底并反射回来经过了较长的等离子体区域，因而此时单站RCS衰减比较大；在入射角比较大的情况下，钝锥单站RCS在无等离子体时值的附近震荡.

［1］MARINI J W.On the Decrease of the Radar Cross Section of the Apollo Command Module due to Reentry Plasma Effects［R］.NASA TN D-4784，1968.

［2］CHURCHILL W J.Progress in reentry communications［J］.IEEE Transaction on Aerospace and Electronic Systems，1971，9：879-894.

［3］BHASKAR C，SHASHANK C.Three-dimensional computation of reduction in radar cross section using plasma shielding［J］.IEEE Trans on Plasma Science，2005，33（6）：2027-2034.

［4］HAYAMI R A.The application of instrumented light gas gun facilities for hypervelocity aerophysics research［C］//17th Aerospace Ground Testing Conference.Nashville，July 6-8，1992.

［5］LUEBBERS R J，HANSBERGER F A.A frequency dependent finite difference time domain formulation for dispersive materials［J］.IEEE Trans EMC，1990，32（3）：222-227.

［6］YU Zhefeng，ZHOU Lezhu，XIA Mingyao，Effect of plasma on the RCS of three dimensional objects［C］//Progress in Electromagnetics Research Symposium.Beijing，2004，August 23-25，2004.

［7］GEORGE T R.Radar Cross Section Handbook［M］.New York：Plenum Press，1970.

［8］金兹堡.电磁波在等离子体中的传播［M］.北京：科学出版社，1978.

［9］庄钊文，袁乃昌，刘少斌.等离子体隐身技术［M］.北京：科学出版社，2005.

［10］ZENG Xuejun，YU Zhefeng，BU Shaoqing.Research on the RCS of hypervelocity model and its plasma sheath［J］.Acta Aerodynamica Sinica，2010，28（6）：645-649.

［11］常 雨，陈伟芳.再入钝锥体绕流流场电磁散射特性分析［J］.宇航学报，2008，29（3）：962-966.CHANG Yu，CHEN Weifang.Analysis of scattering for the flow field of reentry blunted cone［J］.China Journal of Astronautics，2008，29（3）：962-966.（in Chinese）

［12］常 雨，陈伟芳.高超声速圆球绕流流场及其近尾尾迹流场电磁散射特性分析［J］.国防科技大学学报，2009，31（1）：5-10.CHANG Yu，CHEN Weifang.Analysis of the scattering characteristic for the hypersonic flow field with near wake region of sphere［J］.Journal of National University of Defense Technology，2009，31（1）：5-10.（in Chinese）

［13］方 宁，王 谷，王宝发.复杂涂覆目标的角闪烁特性分析［J］.北京航空航天大学学报，2011，37（3）：259-262.FANG Ning，WANG Gu，WANG Baofa.Analysis of glint characters of complex coated target［J］.Journal of Beijing University of Aeronautics and Aetronautics，2011，37（3）：259-262.（in Chinese）

［14］梁世昌，于哲峰，张志成，等.开槽钝锥体及等离子体鞘套的RCS特性研究［J］.实验流体力学学报，2013，27（2）：19-23.LIANG Shichang，YU Zhefeng，ZHANG Zhicheng.Research on the RCS characteristics of blunt-cone with slots and plasma sheath［J］.Journal of Experiments in Fluid Mechanics.2013，27（2）：20-24.（in Chinese）