广义Hamilton系统的Mei对称性与守恒量

郭秀英，刘洪伟，徐中海

(1.吉林市第十八高级中学，吉林吉林132012;2.东北电力大学理学院，吉林吉林132012)

对称性原理是物理学中更高层次的法则，它的重要作用之一就是用来研究系统的守恒量。主要有Noether对称性、Lie对称性及Mei对称性，三种对称性可直接也可间接导致Noether守恒量、Hojman守恒量和Mei守恒量。关于Hamilton系统对称性的研究已取得一些成果［1－2］。传统的Hamilton系统是在偶数维相空间上定义的，这极大地限制了它的应用。后来人们又发展为广义Hamilton系统，因目前尚未找到广义Hamilton系统的相应作用量，致使无法利用Noether对称性来研究其守恒量。可见，利用Lie对称性和Mei对称性研究广义Hamilton系统的守恒量显得尤为重要［3－6］。本文将研究广义Hamilton系统Mei对称性直接导致的新守恒量。并举例说明结果的应用。

1 系统Mei对称性判据和确定方程

广义Hamilton系统的运动微分方程为

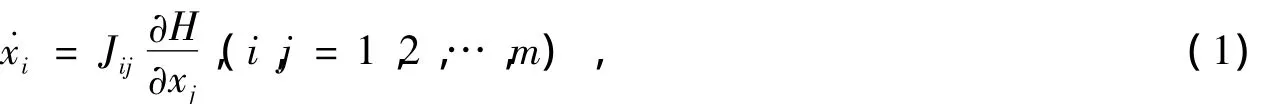
其中:H=H(t，xi)为Hamilton函数，Jij=Jij(xi)满足条件Jij=-Jji，

引入一般无限小变换

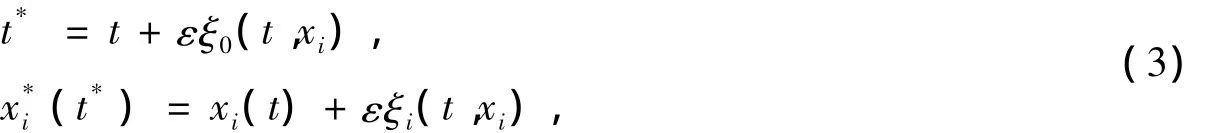
其中:ε为无限小参数，ξ0，ξi为无限小生成元。

定义对于系统(1)，如果动力学函数H=H(t，xi)在无限小变换(3)下有

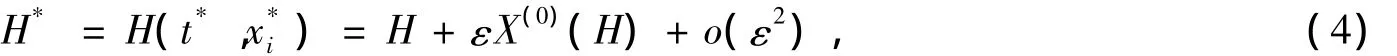
使得系统(1)保持形式不变，即

这种不变性称为广义Hamilton系统的Mei对称性。其中

判据对于系统(1)，如果动力学函数H=H(t，xi)在无限小变换(3)下的生成元ξ0，ξi满足方程

则广义Hamilton系统具有Mei对称性。

3 Mei对称性导致的Mei守恒量

广义Hamilton系统(1)是否还存在其它形式的Mei守恒量及给出如下定理。

定理对于系统(1)，如果动力学函数H=H(t，xi)在无限小变换(3)下的生成元ξ0，ξi满足方程(6)，并且存在规范函数GM=GM(t，xi)满足方程

则广义Hamilton系统(1)的Mei对称性直接导致如下的守恒量

其中是使规范函数GM存在的任意函数。

4 算例

试研究其Mei对称性及其守恒量。

系统(9)的运动微分方程为

考虑一般无限小变换(3)式，由(6)式给出Mei对称性确定方程为

方程组(11)式有如下解

计算X(0)(H)=t，将(12)式代入Mei守恒量存在条件(7)式得

当f=1时，(13)式有解

将f=1和(14)式代入(8)式得新守恒量

5 结论

本文给出了广义Hamilton系统的Mei对称性直接导致的新守恒量，守恒量存在的条件和守恒量的形式更为简洁，并且结果具有一般意义。可以根据规范函数GM的需要适当选取函数f。另外，本文研究了含有时间的广义Hamilton系统的Mei对称性与守恒量，丰富和发展了约束力学系统的Mei对称性理论。

［1］罗绍凯.Hamilton系统的Mei对称性、Noether对称性和Lie对称性［J］.物理学报，2003，52(12):2941－2944.

［2］罗绍凯.奇异系统Hamilton正则方程的Mei对称性、Noether对称性和Lie对称性［J］.物理学报，2004，53(1):5－10.

［3］梅凤翔.广义Hamilton系统的Lie对称性与守恒量［J］.物理学报，2003，52(5):1048－1050.

［4］贾利群，郑世旺.带有附加项的广义Hamilton系统的Mei对称性［J］.物理学报，2006，55(8):3829－3832.

［5］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.

［6］刘洪伟，李玲飞，杨士通.Kepler方程的共形不变性、Mei对称性与守恒量［J］.物理学报，2012，61(20):200202.