高桩梁板码头体系可靠度计算及寿命预测
2013-03-12黄长虹刘凤荣罗劭扬
黄长虹,刘凤荣,罗劭扬
(海军工程大学勤务学院,天津 300450)
随着我国经济的不断发展,港口运输发挥着越来越重要的作用,同时对港口码头的压力越来越大。高桩梁板码头是码头主要结构形式之一。工作在比较恶劣的海洋环境中,钢筋混凝土码头结构在服役期受到钢筋锈蚀、混凝土碳化、腐蚀介质侵蚀、疲劳损伤及材料性能老化等,结构抗力随着时间而衰减[1-2],而且钢筋锈蚀过程和一般大气环境下的钢筋锈蚀过程有很大不同。
体系可靠度是现阶段可靠度研究热点之一。高桩梁板码头主要由面板、纵梁、横梁和桩基组成,其体系可靠度是表示码头整体上所处的状态。随着抗力衰减,其体系可靠度也随之减小。码头体系可靠度研究对于码头加固及寿命预测有很重要的意义。
1 高桩梁板码头钢筋锈蚀过程
钢筋锈蚀是造成钢筋混凝土结构耐久性破坏的重要原因。引起钢筋锈蚀的因素主要有混凝土碳化和氯离子侵蚀,而氯离子侵蚀是造成海工混凝土结构钢筋锈蚀、承载能力降低的首要原因[3]。
1.1 保护层开裂前钢筋锈蚀速度
当氯离子侵蚀的诱导期结束,即在钢筋表面氯离子浓度达到临界值时,钢筋开始锈蚀。在环境相对湿度75%,温度为20℃的条件下,氯离子侵蚀下的钢筋锈蚀速率模型为[4]:

式中:λ为钢筋锈蚀深度,mm/a;w/c为混凝土水灰比;C为混凝土保护层厚度;tp为钢筋开始锈蚀时间。
在钢筋锈蚀后的t时刻,钢筋直径为:

式中:d0为钢筋初始直径。
则钢筋锈蚀后的截面积计算模型为:
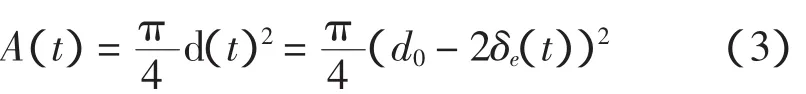
钢筋截面损失率为:

式中:δe(t)为钢筋锈蚀深度,mm;d为钢筋直径。
1.2 保护层胀裂时间
钢筋锈蚀后,锈蚀产物体积变为原来的2~8倍,使保护层混凝土受拉而开裂。
混凝土保护层开裂时的钢筋锈蚀深度[5]:
光圆钢筋:

变形钢筋:
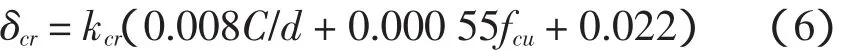
箍筋与网状配筋:
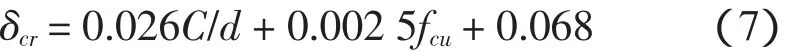
式中:δcr为钢筋混凝土保护层胀开时的钢筋锈蚀深度,mm;kcr为钢筋位置修正系数,角部钢筋取1.0,非角部钢筋取1.35;C为混凝土保护层厚度;d为钢筋直径;fcu为混凝土立方体抗压强度。
1.3 保护层开裂后钢筋锈蚀速率
钢筋保护层一旦开裂,钢筋将直接暴露在空气中,直接和空气中的氧气和水发生反应,锈蚀速率加快。所以,对于码头结构,保护层开裂后的钢筋锈蚀采用牛荻涛钢筋锈蚀计算模型[5]:
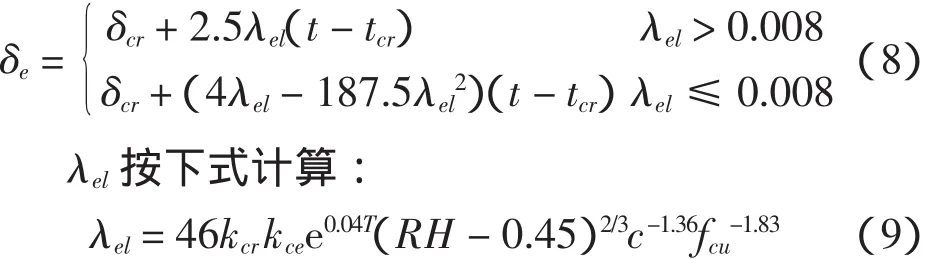
式中:kcr为钢筋位置修正系数,角部钢筋取1.6,中部取1.0;kce为环境条件修正系数,建议:潮湿地区取3.0~4.0,干燥地区取2.5~3.5;T为环境温度(摄氏度);RH为环境湿度,%;fcu为混凝土立方体抗压强度,MPa。
2 钢筋混凝土结构抗力衰减
2.1 锈蚀钢筋屈服强度
随着钢筋的锈蚀,钢筋力学性能下降表现为:主应力应变曲线屈服平台缩短,伸长率和屈服均降低。其时变模型可以表示为[6]:
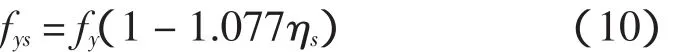
2.2 钢筋与混凝土之间的黏结系数
随着钢筋的锈蚀,钢筋与混凝土之间的黏结性能下降。黏结系数kb按下式计算[5]:
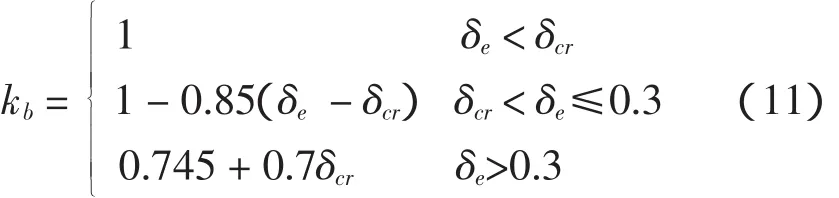
2.3 海工混凝土强度的经时变化
海工混凝土强度并不是一个定值,而是在前几年逐渐增长,其后增长缓慢,5~10 a左右开始下降。混凝土强度随时间的变化为非平稳正态随机过程,其平均值模型为[7]:
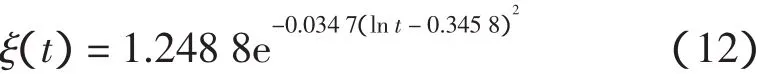
ξ(t)为混凝土强度平均值与28 d时的强度平均值的比值(见图1)。

图1 海工混凝土经时强度曲线
由上述理论,可以推导出受弯构件的抗力时变模型为:

其平均值为:
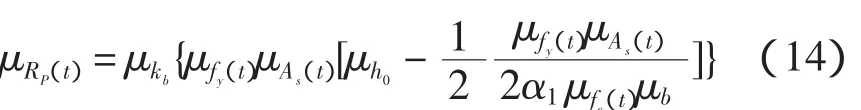
3 基于蒙特卡罗法的码头结构体系可靠度计算
蒙特卡罗法是伴随着计算机而逐步发展起来的一种计算方法,它在计算过程中回避了可靠度分析中的数学困难,不需要考虑极限状态曲面的复杂性。在可靠度分析方法中,被认为是一种比较精确的计算方法。
3.1 蒙特卡罗法基本思想
设随机变量的抽样数为N,每一组随机抽样值对应的功能函数值为Zi,记Zi<0的次数为n,经过足够的抽样后,结构的失效概率为[3]:

3.2 超拉丁立方抽样法
如果蒙特卡罗法采用直接抽样的方法,抽样次数N一般建议满足:

式中:Pf为预先估计的失效概率[8]。
这样就需要很大的样本量,造成计算时间过长。
拉丁超立方抽样方法是一种多维分层抽样方法,它是在各随机变量相互独立的条件下,将各随机变量的概率分布函数按照相同的数目分成几个互不相交的子空间,然后在每个子空间上进行一次独立的等概率抽样。该抽样方法可以有效减少抽样次数,缩短计算时间。其主要步骤是:
1)确定样本数M。
2)把变量分成M个不重叠等概率的子区间,在每个子区间上进行一次独立等概率抽样,各子区间上的抽样值应满足:
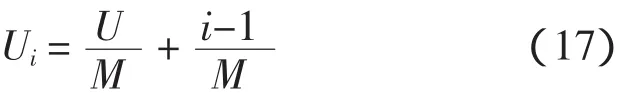
式中:i=1,2,3,…,n;U为 [0,1]区间上均匀分布的随机数;Ui为第i个子区间上的随机数。
3)利用反函数法将各区间上产生的随机数转化为各随机变量的抽样值。
4)将各随机变量的抽样值进行随机组合。
这样便得到了多维随机变量抽样值,对于二维,两个变量5点抽样如图2所示。
由图2可知,拉丁超立方抽样方法避免了在一个子区间上重复抽样,提高了抽样效率。蒙特卡罗法使用拉丁超立方抽样方法进行抽样时,可以缩短计算时间。
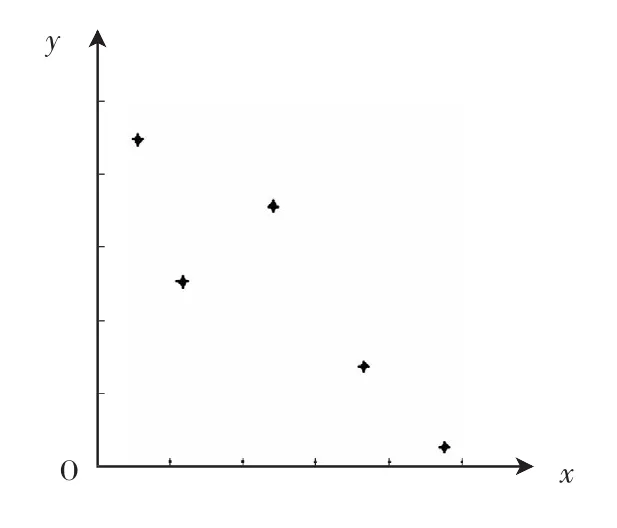
图2 拉丁超立方抽样示意图
3.3 高桩梁板码头结构体系可靠度的计算
应用蒙特卡罗法进行在役高桩梁板码头的体系可靠度计算的主要思路是:码头所承受的荷载及码头构件抗力都是以随机变量形式存在。使用蒙特卡罗法按照荷载和构件抗力所属概率分布类型进行抽样,将抽样值依次施加到码头结构上。按照荷载在码头结构上的传递路径,将构件抗力抽样值和抽样荷载产生的效应值进行比较,当板、纵梁、横梁、桩中有一个构件的抗力值小于荷载效应值时,即认为码头体系失效,并记入码头结构体系失效次数,最后计算出码头结构体系的可靠度指标。
4 算例
某服役9 a的高桩梁板码头,排架间距7m,板厚50 cm,现浇面层厚15 cm,梁为钢筋混凝土叠合梁,桩基采用55 cm×55 cm的空心方桩,横梁保护层厚度平均值为55mm,混凝土立方体抗压强度为45MPa,水灰比0.42,根据其氯离子含量检测值,利用氯离子侵蚀模型计算出结构服役17 a时,横梁钢筋表面氯离子含量达到临界值。钢筋采用螺纹钢筋,横梁纵向钢筋直径为25mm。码头横向排架断面见图3。
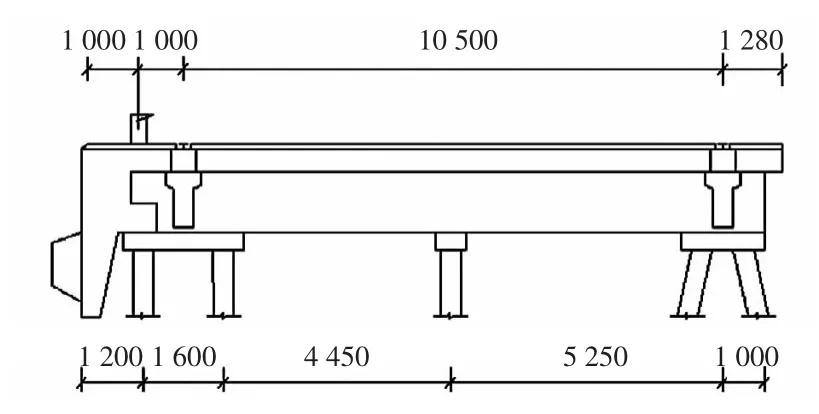
图3 码头横向排架断面图(单位:mm)
氯离子侵蚀下的钢筋锈蚀速率模型为:
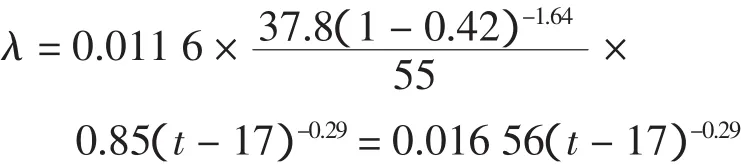
则保护层胀裂时的锈蚀深度为:

钢筋保护层锈胀时间为:t=6.9 a,此时码头运行时间约为25 a。
此时的混凝土碳化深度按照邸小坛碳化模型[9]计算为:

式中:α1为养护条件修正系数,28 d养护取1.0;α2为水泥品种修正系数,普通硅酸盐水泥取1.0,矿渣水泥取1.3;α3为环境条件修正系数。
所以说,对于工作在海洋环境下的钢筋混凝土结构,在保护层锈胀开裂前可以不考虑碳化对钢筋锈蚀的影响。
保护层开裂后,钢筋锈蚀为:
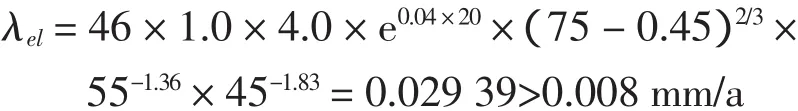
则:δe=0.065+0.029 39 × 2.5 ×(t-24)
图4为横梁纵向钢筋锈蚀深度随时间变化的曲线。
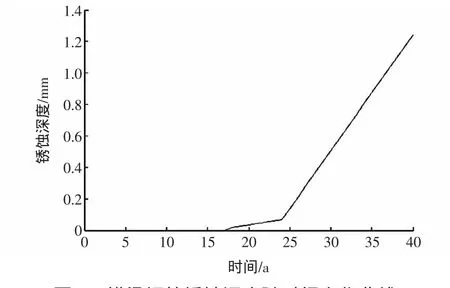
图4 横梁钢筋锈蚀深度随时间变化曲线
将上例中氯离子浓度检测数据,作为该码头的氯离子侵蚀情况。在堆货荷载和自重作用下,借助于Matlab软件,使用蒙特卡罗法计算码头体系可靠度。由于钢筋锈蚀,混凝土强度衰减引起的码头体系可靠度变化曲线如图5所示。

图5 码头体系可靠度随时间的变化
当可靠度指标降低到0.8β0时[10],认为结构使用寿命结束。由图5可以看出,码头的寿命大概是25 a。
5 结语
1)氯离子侵蚀是造成码头钢筋锈蚀的首要因素。氯离子侵蚀首先到达钢筋表面,引起钢筋锈蚀,进而造成保护层开裂。而此时碳化深度不到2mm。保护层开裂后,钢筋暴露在空气中,锈蚀速度加快。钢筋锈蚀不仅造成钢筋面积减小,而且引起钢筋力学性能降低,钢筋与混凝土之间黏结力下降。
2)在蒙特卡罗法基础上,抽样阶段使用超拉丁立方抽样方法,可以精确的计算出高桩梁板码头体系可靠度,同时回避了体系可靠度计算时各失效模式相关性的问题,更加易于计算。
3)一旦钢筋开始锈蚀,高桩梁板码头体系可靠度将以很快的速度下降,因此氯离子侵蚀是影响码头寿命的主要因素,所以对码头采取氯离子侵蚀的防护措施是非常必要的。
[1] 黄长虹.在役高桩码头耐久性评估方法研究[D].天津:天津大学,2003.
[2] 张莉.在役高桩码头可靠度分析与剩余使用寿命预测[D].天津:天津大学,2011.
[3] 王元战,田双珠,王军,等.不同环境条件下考虑荷载影响的氯离子扩算模型[J].水道港口,2010(4):125-130.
[4] KIM ANH T VU,MARK G STEWARK.Structural Reliability of Concrete Briges Including Improved Chloride-induced Corrosion Models[J].Structural Safety,2000(22):313-320.
[5] 牛荻涛.混凝土结构耐久性与寿命预测[M].北京:科学出版社,2003.
[6] 牛荻涛,卢梅,王庆霖.锈蚀钢筋混凝土梁承载力计算方法研究[J].建筑结构,2002(10):14-17.
[7] 牛荻涛.海洋环境下混凝土强度的经时变化模型[J].西安建筑科技大学学报,1995(3):49-52.
[8] 李清富,高健磊,乐金朝,等.工程结构可靠性原理[M].河南:黄河水利出版社,1999:45-140.
[9] 邸小坛,周燕.混凝土碳化和钢筋锈蚀原因及防止措施[J].工业建筑,1989,1(6):7-10.
[10] 赵国藩,金伟良,贡金鑫.结构可靠性理论[M].北京:中国建筑工业出版社,2000:1-138.
