基于HHT的锚杆锚固质量声波无损检测

刘东辉，米 博，赵东松，孙晓云

（1.河北科技大学电气工程学院，河北石家庄 050018；2.石家庄铁道大学电气与电子工程学院，河北石家庄 050043）

岩土锚固由于具有合理利用岩土的自身强度和自稳能力，简化结构体系，减小结构体积，提高结构物的稳定性，占用地较少、安全施工、缩短工期、降低造价等优点［1］，锚固技术在中国的铁路、公路、矿山及水工隧道中得到广泛应用。对锚杆锚固质量、锚杆的完整性以及锚杆中的应力状态进行实时监控是非常有必要的一项工作。由于传统检测方法的种种不足，所以寻求一种能快速、实时检测锚杆锚固质量及其受力情况的技术，是保证围岩加固质量及其稳定性的必要前提，也是中国目前岩土加固工程急需解决的关键技术问题。

本研究对检测到的锚杆信号进行HHT分解，和提取的首波信号进行相关处理，得到反射信号的具体时间，以此来确定锚杆参数。

1 HHT

HHT是一种根据信号的尺度特征来分解信号，从而对信号自适应的频带进行划分［2］。该方法拥有较好的局部适应性，而通过引入瞬时频率，可以同时分析时频两方面的信号，从而能灵活、有效地处理信号。

经验模态分解（EMD）是HHT的基础。第1步先用EMD对信号作分解，这样就可以得到一连串的表征信号时间尺度特征的IMF信号ci和1个余量rn：

式中的i表示用EMD分解后得到的IMF模态的编号。而IMF可以是非平稳信号或者是平稳信号［3］。因为IMF强调局部时间尺度，希尔伯特变换依然存在意义。用希尔伯特对IMF作变换，假设IMF信号为c（t），那么解析信号为

幅值函数为

相位函数为

式中：幅值函数表示信号每个采样点的瞬时幅度；相位函数表示信号中所有采样点的瞬时相位，求导后就是瞬时频率：

2 实验结果分析

利用声频应力波方法检测锚杆信号，分别对其进行傅里叶变换和希尔伯特黄变换得到2组数据，再加上原始信号，对信号用数字信号处理的方式进行分析，并将3种分析结果进行比较。

锚杆无损检测方法首先利用四角锤敲击锚杆，利用传感器接收反射信号，经过数据采集装置送入计算机，进行信息处理［4］。

测试锚杆长度为1 800mm，锚固部分1 100mm。随机敲击锚杆，得到不同的反射波信号，检测频率为44 100Hz。图1为不同材质的四角锤敲击得到的5组反射信号，图2为其中1组原始信号。

图1 反射信号Fig.1 Reflection signal

从该信号的原始波形中，只能看出信号的时域特性，因此需要利用分析手段对信号进行处理，从而得到其频域特性，见图3。

图2 sR25-n1Ri22原始信号的波形Fig.2 sR25-n1Ri22’s original signal waveform

图3 信号频谱Fig.3 Signal spectrum

2.1 FFT频率计算

傅里叶变换是传统的频域分析方法，首先对信号进行傅里叶变换，从而得到信号的频谱。

同时求得信号的基波频率为3 278.034 2Hz，基波幅值为8 289.527 4，基波相位：单位弧度为1.775 5。从频谱中可以看出，信号有2个主要突出的频率和1个明显的反射波频率。通过读取可得出3个频率分别为3 278，4 257，5 277Hz。

据应力波反射法，在靠近激发点处接收到的反射波，其传播路径大致是杆长（L）的2倍。来回反射一次的周期应等于传播路径（2L）除以杆中波的速度（C）。频率是周期的倒数，故与某长度相应的频率f为［5］

式中：f为频谱图上该峰所对应的频率值；C为被测体声速。从文献［6］可知，浇注段平均波速为3 571 m／s，通过式（6），可根据频差来求取锚杆检测长度。

由此可计算得锚固段长度为1.01m，而实际浇注长度是1.1m，则测试误差为8.1%。

2.2 HHT及原始信号的相关计算

HHT是近年来新的非平稳信号分析方法。它根据数据自身的时间尺度特征把信号分解为有限个固有模态函数（intrinsic mode function，简称IMF），分解得出的所有IMF分量都突出了信号的局部特征［7］，再对各模态分量进行希尔伯特变换从而得到信号能量在时间尺度上的分布规律，实现信号动力特性的量化提取［8］。

希尔伯特黄变换的主要创新是固有模态（IMF）的提出和经验筛法（EMD）的引入。通过EMD，把信号分解成为IMF的和，对所有IMF进行希尔伯特变换就能得到有意义的瞬时频率，从而可以给出频率变换的精确表达［9-11］。

对被测信号进行HHT分解，得到信号的特征值（为第2个或第3个尺度的分解信号）［12］如图4所示，图4得到的是经过HHT特征值提取后的信号。

图4 HHT分解信号Fig.4 HHT decomposition

锚杆测试信号波形图中第1个波组命名为首波，它是在每次敲击时被安置在杆头的传感器首先接收的信号，后面每间隔一段出现的波组是在锚杆中传播的反射波［13-14］。图5为从图4中提取的首波信号，利用首波和反射波特征提取信号作互相关，提取其底端反射信号，进而得到浇注段的长度［15-16］。图6为利用HHT算法得到的特征值信号。

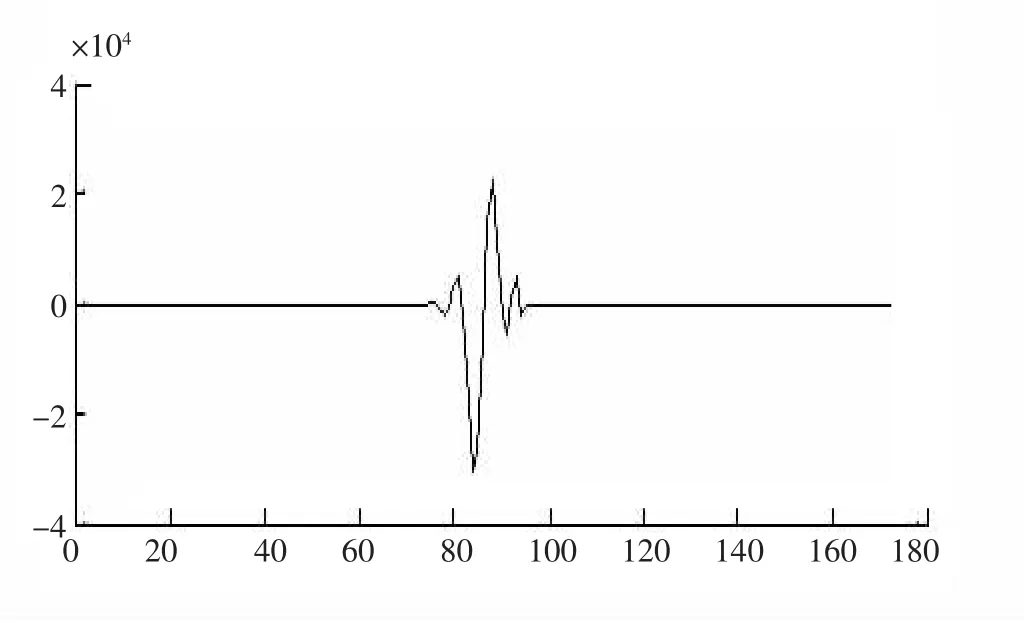
图5 首波提取信号Fig.5 First wave signal

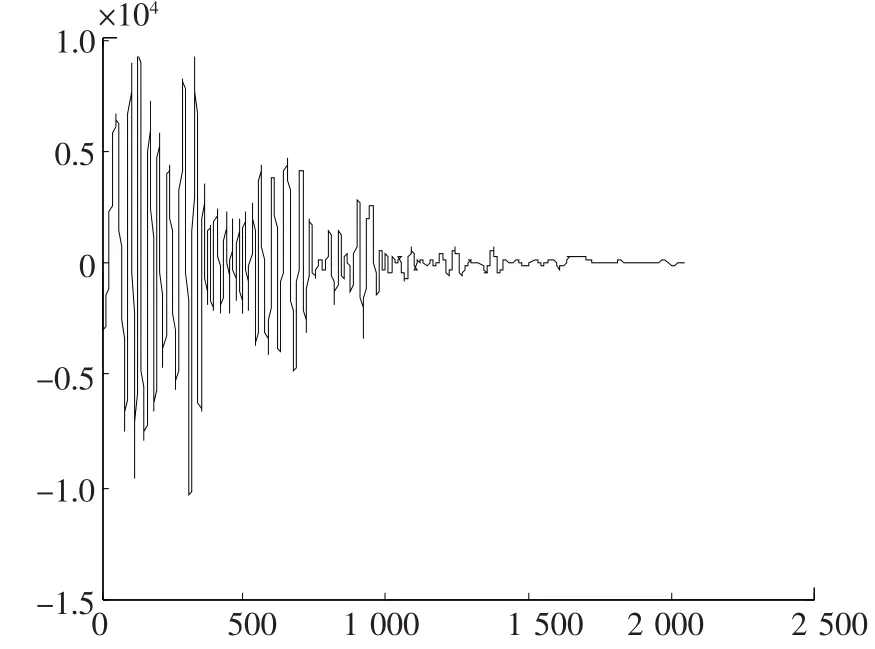
图6 HHT提取的信号Fig.6 HHT extraction of signal

图7为首波与特征值信号之间的相关图，图8为首波与原始信号的相关图。

从图7中可知底端反射时间是1.52ms，而固端反射时间为0.92ms，从文献［11］可知，浇注段平均波速为3 571m／s，可算出浇注段长度分别为1.07m，实际浇注长度为1.1m，则测试误差为2.7%。

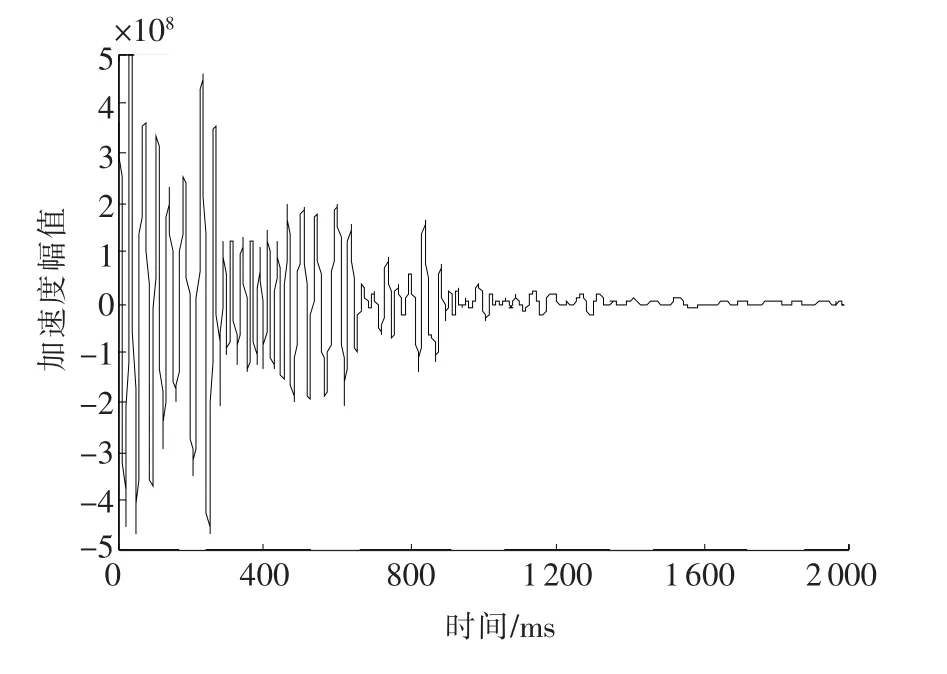
图7 首波与特征值信号之间的相关图Fig.7 Correlation diagram of first wave and eigenvalue signal

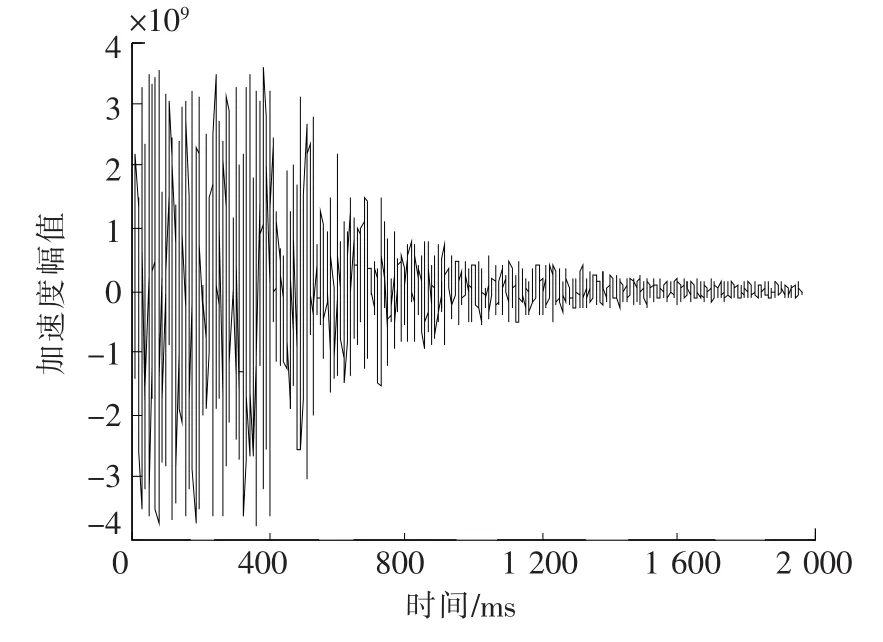
图8 首波与原始信号的相关图Fig.8 Correlation diagram of first wave and original signal

由于信号未经小波除噪，信号中含有大量杂波，从图8中可知底端反射时间是1.45ms，而固端反射时间为0.89ms。从文献［11］可知，浇注段平均波速为3 571m／s，可算出浇注段长度为0.99m，而实际浇注长度为1.1m，测试误差为10%。

3 结 语

分别应用FFT和HHT方法分析了锚杆信号，因为HHT从信号自身的尺度特征入手来进行信号分解，实现了对信号频带划分的自适应，同时具有良好的局部适应性；瞬时频率的引入使其可以分析信号的时频2个方面，加强了信号处理的灵活性和有效性。分析结果表明，首先提取首波信号，然后将检测信号作HHT分解，和提取的首波信号作相关，能更好地检测到反射波信号，得到较为准确的锚杆质量参数。

／References：

［1］ 王 春，彭东林.Hilbert-Huang变换及其在去噪方面的应用［J］.仪器仪表学报，2004，25（sup）：42-45.WANG Chun，PENG Donglin.The Hilbert-Huang transform and its application on signal de-noising［J］.Chinese Journal of Scientific Instrument，2004，25（sup）：42-45.

［2］ 仲佑明，秦树人，汤宝平.一种振动信号新变换法的研究［J］.振动工程学报，2002，15（2）：233-238.ZHONG Youming，QIN Shuren，TANG Baoping.Study on a new transform method for vibration signal［J］.Journal of Vibration Engineering，2002，15（2）：233-238.

［3］ HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc Roy Soc London A，1998，454：903-909.

［4］ KIZHNER S，BLANK K，FLATLEY T，et al.On certain theoretical developments underlying the Hilbert-Huang transform［A］.IEEE Aerospace Conference Proceedings［C］.Piscataway United States：Institute of Electrical and Electronics Engineers Computer Society，2006.167-169.

［5］ 盖 强，张海勇，徐晓刚.Hilbert-Huang变换的自适应频率多分辨分析研究［J］.电子学报，2005，33（3）：563-566.GAI Qiang，ZHANG Haiyong，XU Xiaogang.Study of adaptive frequency multiresolution analysis of the Hilbert-Huang transform［J］.Acta Electronica Sinica，2005，33（3）：563-566.

［6］ SATISH L，ZAENGL W S.Artificial neural networks for recognition of 3-d partial discharge patterns［J］.IEEE Trans on Dielectrics and Electrical Insulation，1994（2）：265-275.

［7］ 罗奇峰，石春香.Hilbert-Huang变换理论及其计算中的问题［J］.同济大学学报（自然科学版），2003，31（6）：637-640.LUO Qifeng，SHI Chunxiang.Hilbert-Huang transform and several problems in its calculation method［J］.Journal of Tongji University（Natural Science Edition），2003，31（6）：637-640.

［8］ SUN Xiaoyun，LIU Donghui.A new effective method removing measurement noise in eddy current nondestructive detecting［J］.International Journal of Applied Electromagnetics and Mechanics，2010，33：1 173-1 177.

［9］ CHENG Jiulong，SUN Xiaoyun，FENG Li，et al.Experimental study on non-destructive testing of rock bolts based on pseudo-random signal［J］.Safety Science，2012，50（4）：783-786.

［10］ 杜爱明，王 彬，杨润海.Hilbert-Huang变换中的一种端点处理方法［J］.地震研究，2007，30（1）：54-58.DU Aiming，WANG Bin，YANG Runhai.A boundary-processing method in Hilbert-Huang transform［J］.Journal of Seismological Research，2007，30（1）：54-58.

［11］ TADOLINI S C.Mine roof bolt load determinations utilizing ultrasonic measurement systems［J］.CIM Bulletin，1990，83（4）：49-54.

［12］ IVANOVIC A，NEILSON R D，RODGER A A.Numerical modeling of single tendon ground anchorage systems［J］.Geotech Eng，2001，149（2）：103-113.

［13］ BEARD M D，LOWE M J S.Non-destructive testing of rock bolts using guided ultrasonic waves［J］.International Journal of Rock Mechanics and Mining Sciences，2003，40：527-536.

［14］ BEARD M D.Guided Wave Inspection of Embedded Cylindrical Structures［D］.London：University of London，2002.

［15］ BEARD M D，LOWE M J S，CAWLEY P.Ultrasonic guided waves for inspection of grouted tendons and bolts［J］.Journal of Materials in Civil Engineering，2003，15（3）：212-218.

［16］ 程军圣，于德介，杨 宇.基于EMD的信号瞬时特征的小波分析方法［J］.地震工程与工程振动，2004，24（2）：181-186.CHENG Junsheng，YU Dejie；YANG Yu.Signal instantaneous attribute analysis using wavelet transform based on EMD［J］.Earthquake Engineering and Engineering Vibration，2004，24（2）：181-186.