非相对论情况下真空中静电场压强概念的探索
2013-03-11吕庆敖陶青青
吕庆敖 陶青青
(军械工程学院弹药工程系,河北 石家庄 050003)
在非相对论情况下,关于电荷之间如何相互作用的问题,物理学界一般有两种观点.一种是早期的,认为电荷与电荷之间是不通过任何媒介直接发生的“超距作用”,即:电荷⇔电荷.另一种晚期的观点则认为电荷是通过某种叫“电场”的媒介发生相互作用的,即:电荷⇔电场⇔电荷[1-5],并按照带电量为q的检验电荷受力F 来定义电场强度E =F/q.随着科技的进步,电场观点被绝大多数人认可.
沿袭主流观点,我们认为电荷是通过电场来发生相互作用的,且电场作为一种物质是客观存在的,电场能够传递力.但是,关于电场自身应力以及力传递的问题,从现有文献看,至今还没有定量的解析表述,即:“电荷⇔电场⇐……⇒电场⇔电荷”中间的环节是模糊的.电场内部一个区域与相邻的另一个区域之间的相互作用仍处于不明确状态.本文在磁场压强概念的基础上,采用与磁场压强理论类比的方法,尝试探索电场内在应力及力的传递问题.
1 电场压强的概念假设
在磁约束受控核聚变及高温等离子体物理领域[6]和机电动力学领域[7]都有系统的磁压强概念和基本理论,其概念的基础模型是磁力线管,即沿空间任意一束磁力线均可切割成由3个曲面封闭包围的管状磁力线束,又叫磁力线管.3个曲面分别是顶面、底面、侧面,穿过磁力线管的每条磁力线均从底面穿入、从顶面穿出.磁场在封闭表面上的磁压强分布决定了整个磁力线管受到的体积力.更具体地,作用于曲面的磁压强有统一的表达式,即pB=0.5B2/μ0,其中,B 是磁场空间局部的磁感应强度;μ0是真空的磁导率.磁压强理论还在磁通压缩发电机领域[8-9]有具体应用.

表1 电场与磁场基本参数的对比
大家知道电磁学中电场与磁场呈现出一定的对称性.如表1所示,电场强度E 与磁感应强度B 对应,直接决定作用力;按照库仑定律和电场强度定义,电场源于电荷q或电荷密度ρ;按照毕奥-萨伐尔定律磁场源于电流强度I 或电流密度i;真空介电常数ε0与磁导率μ0对应.尤其电场和磁场的能量密度也对应,分别为0.5ε0E2和0.5B2/μ0.另一角度,按照分子运动学理论,压强对体积积分就得到机械功,能量密度对体积积分就得到能量,考虑功能转化,压强与能量密度也是对应的.磁场压强表达式与磁场能量密度表达式的一致性就是功与能一致的具体体现.基于以上类比,笔者在这里大胆假设电场压强表达式也与电场能量密度一致,即量叠加原理,总电场强度E 可表示为

在表1所示的电场压强pE处填上0.5ε0E2,电磁参数就相当对称了.还有,与磁力线管相类似,笔者假设的电力线管及电场压强在电力线管表面分布如图1所示.

图1 电力线管结构及其表面的压强分布
图1所示的是电场空间中一束电力线(又叫电场线)被想象地“切割”成电力线管,电力线管由三个曲面包围,即:顶面St、底面Sb、侧面Ss.穿过电力线管中的每根电力线都从底面Sb进入,都从顶面St出去.作用在顶面及底面的电场力压强都与电力线平行,垂直于这两个曲面由内向外,好像要拉伸电力线管变长.而作用在侧面Ss的电场力压强垂直于电力线,由外向内垂直于侧面,好像要使电力线管变细.三个曲面上的压强大小均由式(1)表达,其中E 为电场空间局部的电场强度.根据高斯定理,封闭曲面上的压强分布就完全决定了整个电力线管受到的电场力.
2 电场压强的可行性及可靠性证明
直接证明电场力压强假设是不方便的,甚至是不可能的.为此,采用与典型的、有代表性的列举方案进行对比的方法.
改写电场强度的定义E=F/q 就得到F =qE.虽然上述力的表达式来自于电场强度的定义式,但现在已经成了求解静电力问题的最基本公式.按照微积分的思想,当微小带电体小到一定的程度时,可以把不均匀电场当作匀强电场来处理.这样,匀强电场E0中带电量为q的微小带电体受力为

应当指出的,任何宏观带电体在电场中的受力问题都可以按照微积分的观点采用式(2)把q换成ρ 进行积分求解.换句话说,式(2)具有普遍适用性和广泛的代表性.
如果按照电场压强假设得到电场中电荷受到的电场力的表达式与式(2)相同,则由于式(2)的广泛适用性和可靠性,那么电场力压强也具有相同的适用性,电场压强假设也就得到了证明.具体地,把电场力压强假设用于匀强外电场中点电荷的受力情况,根据外电场建立坐标系O-xyz,如图2所示.

图2 匀强外场、点电荷及积分球面的分布图

其中,

式中,α为电场强度与x 轴的夹角.
根据电力线管及电场压强的概念,把图2 所示的积分球面看作一些连续排列的小电力线管阵列,如图3所示.
在图3所示的微观球面矢量S 表示实际积分球面的局部,在球面上沿电场强度矢量E 方向划分出一系列连续分布的电力线管.根据电力线管压强公式(1)可求得积分球面的受力情况.
先求沿电场方向的纵向拉力压强对微分球面的作用,沿x 轴分量和y 轴分量分别为

图3 微观球面矢量S、电场强度矢量E、电力线决定的电力线管之间的空间关系

再求与电场方向垂直的横向压迫压强对微分球面的作用,沿x 轴分量和y 轴分量分别为
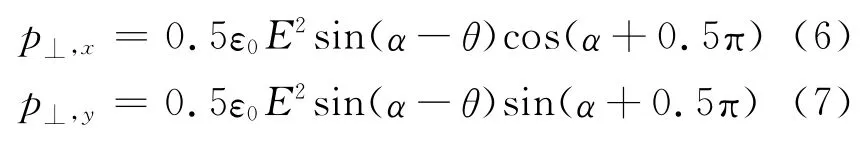
为方便计算,以O 为坐标原点,以Ox 为对称轴引入球坐标系,由式(4)和式(6)得到电场压强力沿对称轴x 坐标上的分量为

(其中,dS=Rdθ·Rsinθdφ,0≤φ≤2π)
将式(8)代入有关α的表达式(3)及(3′),积分后得到

由式(5)和(7)经严格推导,对于轴对称结构的电场力沿与对称轴垂直方向的合力Fy=0,Fz=0.故作用于电荷上总的电场压强力为

电场压强力式(10)与经典表达式(2)明显一致.理论上,一切静电力问题都可以用匀强电场中电荷受力的通俗表达式(2)来解决,式(2)被认为是正确无疑的.电场压强力式(10)与式(2)一致,它反映了电场压强理论式(1)的普遍适用性和正确合理性.
3 结论和讨论
本文在磁场压强概念的基础上,通过类比方法提出了电场压强概念.并通过典型的有代表性的匀强电场中点电荷受力情况实例,运用对比分析方法,论证了电场压强概念的可行性和可靠性.电场压强概念的引入深化了对电场的认识.
(1)从本文内容上看,静电场中电场压强处处满足牛顿第三定律,这是现有电场概念所忽略的.并且在电荷区域获得了与普通物理中F=qE一致的表达式;在没有电荷的区域,任何空间或物体受到电场压强的作用矢量和为零.电场压强假设与现有已知事例均不矛盾.非相对论情况下,电场压强概念能够解决几乎所有电荷受电场力作用的问题.
(2)静电场内引入了电场压强,但是电场对于处于它内部的电中性物体不产生相互作用,从这个意义上说,电场本身像个看不见摸不着的弹性支架,但检验电荷能够探测到它的客观存在.
(3)如果库仑定律说明了“电荷”对“电荷”的相互作用,可以是“超距的”;现代电场概念的引入,把一个“电荷作用”引申为“电场作用”,解决了“电荷”与“电场”之间的相互作用问题;而电场压强概念把另一个“电荷作用”也引申为“电场作用”,把电荷间相互作用进一步深化为“电场”对“电场”的直接接触作用.从“超距作用”过渡到“接触作用”,是对电场认识的进一步深化.
(4)本文仅限于物体速度远小于光速的非相对论情况下电场内在的力学特性探索.对于相对论情况下电荷受力问题已经有成熟的理论[2,10].关于从非相对论情况向相对论情况的过渡问题是下一步工作的方向.
[1]赵凯华,陈熙谋.电磁学[M].北京:高等教育出版社,1985.
[2]张三慧.大学物理学[M].3 版.北京:清华大学出版社,2008.
[3]毛骏健,顾牡.大学物理学[M].北京:高等教育出版社,2006.
[4]潘根.基础物理述评教程[M].北京:科学出版社,2002.
[5]康颖.大学物理[M].长沙:国防科技大学出版社,1997.
[6]马腾才,胡希伟,陈银华.等离子体物理原理[M].合肥:中国科学技术大学出版社,1988.
[7]邱家俊.机电分析动力学[M].北京:科学出版社,1992.
[8]吕庆敖,高敏,雷彬,等.磁通压缩发电机的基本问题(Ⅰ)[J].高电压技术,2006,32(6):64-66.
[9]Lv Q -A,Lei B,Gao M,et al.Magnetic flux compression generator as future military pulsed power supply[J].IEEE Trans.Magn.,2009,45(1):545-549.
[10]郭硕鸿.电动力学[M].北京:高等教育出版社,1997.
