一种基于FPGA 的数字EIT 系统的实验研究
2013-03-10孙晓彤郝会玲
孙晓彤 郝会玲 沙 洪
(中国医学科学院生物医学工程研究所,天津300192)
引言
电阻抗断层成像技术(electrical impedance tomography,EIT)是继形态、结构成像之后的新一代成像技术,该技术具有功能成像、无损伤和医学图像监护三大突出特点[1],在近十几年受到国际学术界的广泛关注[2-3],并在心、脑、肺血管及循环系统功能检测、肿瘤的早期发现[4]及诊断与胃动力功能的检测[5]等方面表现很大的优势,呈现很好的应用前景。EIT 技术自上世纪70 年代起已经有几十年的发展,在试验和临床上都取得了较大的成就。如英国Sheffield 大学组建的Mark 系列系统[6]和美国纽约Rensselaer Polytechnic Institute 建立的ACT 系统都取得了很好的成像效果[7]。在国内如第四军医大学、天津大学和中国医学科学院生物医学工程研究所等也在成像算法和硬件系统的设计等方面取得了研究成果[8-10]。
EIT 系统中采用FPGA 不仅可以实现各种复杂的逻辑运算为系统提供激励信号,而且还可以为后续的解调模块提供参考信号,使系统集成度提高。另外采用FPGA 可实现14 ~16 位的高精度激励电流源,信噪比可达到78 ~100 dB,输出频率范围可达到0 ~1.5 MHz[11],使系统性能在宽带和精度上有很大提升。而在以复阻抗测量为目的的EIT 系统中,采用传统的模拟解调方法输出信号的相位误差一般只能做到2°到3°,幅度误差约为0.5 dB[12],而采用FPGA 实现的数字化解调技术,不仅可以有效地提取复阻抗实部和虚部的信息,而且误差范围都在1%以内,这也是EIT 一直研究的热点。
本课题以多频复阻抗生物电阻抗测量系统为研究目标,采用FPGA 和DDS 技术设计正弦信号发生器,选用THS4201 改进的Howland 电路构建了高输出阻抗的恒流源,在高激励频率情况下保证系统有较宽的频带和输出阻抗,并采用FPGA 设计了数字化正交解调电路,实现复阻抗全信息测量,具有精度高、抗干扰能力强的特点。
1 方法
系统设计中选择ALTERA 公司的Cyclone 系列芯片EP2C35F672C6,采用Verilog HDL 硬件描述语言。系统结构如图1 所示。首先在FPGA 内由数字逻辑设计产生数字信号发生器,经D/A 转换和低通滤波获得模拟电压信号,该信号经过V/I 变换生成模拟电流信号,再通过开关阵列和电极加载到生物组织上进行激励。由测量电极采集的模拟电压信号经信号调理电路和A/D 转换后送入FPGA 中进行数字正交解调,获取被测阻抗的实部和虚部信息。
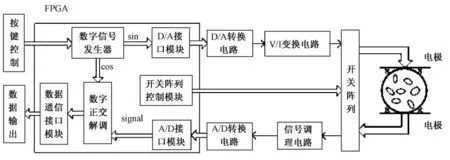
图1 数字化电阻抗测量系统结构Fig.1 Structure of digital electrical impedance measurement
由正弦信号发生器和V/I 变换共同组成的激励电流源和数字正交解调部分是整个测量系统中的重中之重,影响整个系统的准确度和精度,因此本研究主要对激励电流源和数字正交解调进行研究和分析。
1.1 激励电流源
正弦信号发生器的设计基于FPGA 和DDS 技术,如图2 所示。DDS 技术具有频率分辨率高,相位噪声低、频谱纯度好、易于集成、合成信号的频率范围宽等优点[13]。DDS 模块主要包括相位累加器和ROM 表。在时钟的同步下,每一个时钟周期,相位增加一个增量Δθ,累计后的相位与初始相位相加;然后在正余弦表中查找对应相位的幅度值,从而输出数字正余弦信号。DDS 有3 个重要的参数:相位增量Δθ,线性表深度2β,系统时钟频率fclk,输出信号的频率为fout= fclk× Δθ/2β。本系统输出信号的频率和初始相位均可调。综合考虑相位分辨率、带宽和占用的存贮空间等因素,将线性表的深度定为213。若系统时钟为50 MHz,数据位数为14 bit,相应输出信号的频率为6.1 ~390.6 kHz。本设计中输出信号的相位和频率都可调。
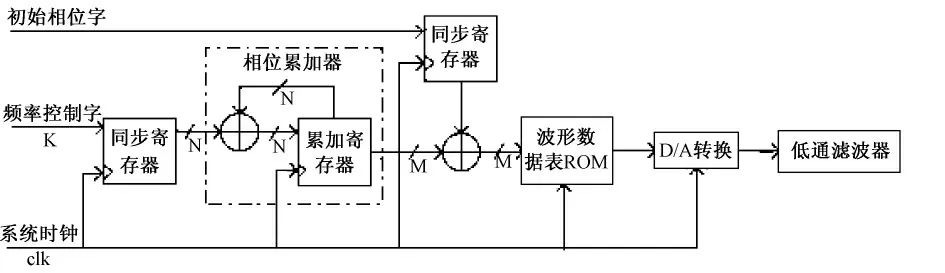
图2 DDS 结构Fig.2 Structure of DDS
本生物电阻抗测量系统采用电流激励-电压测量的方式,激励源为电流源,要求具有高输出阻抗。系统采用由THS4021 改进的Howland 电路[14]构建恒流源,如图3 所示。它是在原Howland 电路基础上加一个反馈电阻R2,减少了负载变化对电流源的影响,提高电流源的输出阻抗。因此本研究中分别测量了恒流源在不同负载下输出电流幅值的频率响应和在不同频率下电流源的输出阻抗,多角度对恒流源性能进行分析。
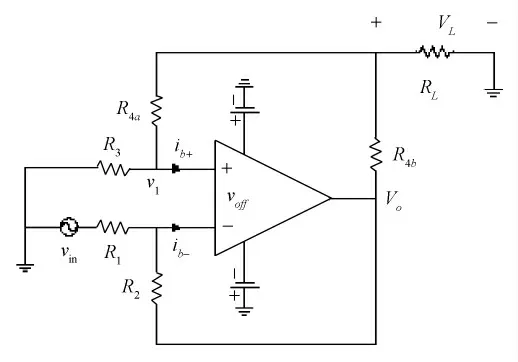
图3 改进的Howland 电路结构图Fig.3 Configuration of Improved Howland circuit
由于高频率的激励信号和宽测量范围,系统在后续的电路中要求选用的D/A 和A/D 芯片具有高速、高位、高精度、低功耗等特点。其中D/A 转换器件选用AD976 芯片,它具有14 位分辨率和采样率高达125 MSPS 的双D/A 通道,每个通道可单独或交叉工作。A/D 转换器选用具有14 位分辨率和采样率高达65 MSPS 的双A/D 通道的AD9248[15]芯片,工作电压3.3 V 下功耗仅为330 mW。A/D 和D/A 芯片均可兼容于DE2 开发板。
1.2 数字化解调
在EIT 测量中,被测电阻抗信息调制在激励信号上,需要通过对该调制信号的解调才能获取被测阻抗的实部和虚部信息。采用FPGA 实现数字正交解调[16],其原理如图4 所示。解调过程为测量信号V(t)经过A/D 之后成为数字化信号V(n),DDS 模块产生与V(n)同频率且相互正交的参考信号P(n)和Q(n),它们分别与V(n)进行一个周期内的乘累加,从而得到被测阻抗的实部信息R 和虚部信息I。
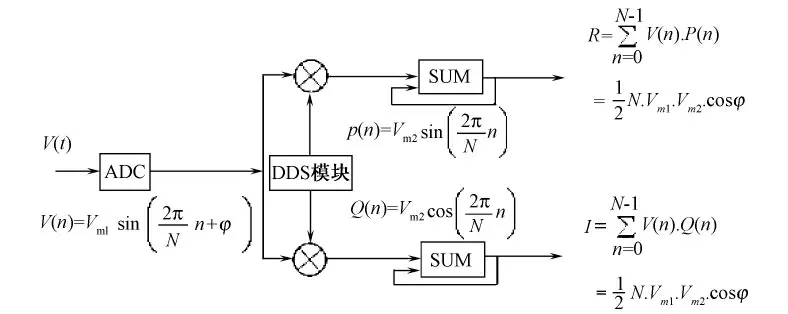
图4 数字化解调Fig.4 Digital demodulation
采用DDS 方法在FPGA 内部构建的数字信号发生器可产生与被解调信号同频的正交参考信号,消除模拟正交解调中参考信号的频差,提高解调精度。该技术可以在一个周期内直接给出被测阻抗信息,不需要低通滤波,提高了系统的动态性。在FPGA 设计中,虽然激励信号和参考信号采用相同的相位值进行查表,但由于D/A 和A/D 之间的电路存在延时,使信号V(n)与同步的正交参考信号出现偏差,产生同步时延,本研究通过定标获得输出D/A 信号和输入A/D 信号采样的时间间隔,消除因不同步而引起的解调相位误差。此外,还可通过在多个周期内进行数字正交解调的方法来减少高速采样过程中产生的随机误差,通过校准和补偿的方法减少系统误差。
例如在本研究中一个待解调电压信号的幅度A为2,相移为π/6,将经ADC 采样后的256 个离散量化数据值存储于ROM 中,经过正交解调电路后可以得到输出十进制表示的Q 和I 分别为242 和431,则计算对应的幅度值和相位值分别是1.93 和0.5116,幅度和相位的相对误差分别达到3.46%和2.29%,幅度误差小于0.1,相位误差小于1°,有效提高了解调信号的精度。
假定A/D 工作在满量程状态,设D = FS,FS 表示ADC 的满量程输入值。若相位β =0,Q 为ADC的转换位数,参数N 为计算出一个I(或Q)值所需的采样点数,则可通过下式来计算数字正交解调的信噪比[17]
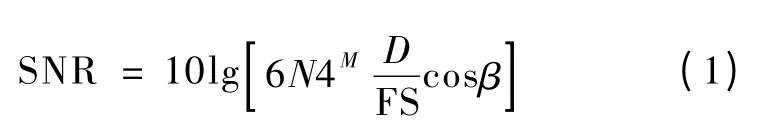
若取N =256,则理论上可实现正交序列解调器120 dB 的输出信噪比。
1.3 盐水槽实验
盐水槽为16 电极系统,采用相邻激励-相邻测量模式进行测量。在进行盐水槽实验时,被测场域是一个直径为20 cm、高20 cm 的圆柱形盐水槽,槽内壁上均匀分布16 个长30 mm、宽15 mm、厚0.5 mm 的电极,通过电缆与阻抗测量平台相连。在实验中,盐水槽中盛有电导率为500 μS/cm 的氯化钠溶液,采用相邻电流激励相邻电压测量的模式,其中激励电流的频率为24.4 kHz,峰峰值为2 mA。以直径25 mm 电导率约0.1 μS/cm 的环氧树脂棒为成像目标,用实验室现有的EIT 成像软件系统对测量所得的数据进行成像。
2 结果
2.1 恒流源的测量结果
恒流源的输出电流在不同负载条件下,即R 分别为0.5、1、1.5、2 kΩ 的频率响应如图5 所示。可知,在频率低于1 MHz 时,由THS4201 构成的电流源在不同负载上面的输出电流的幅值基本保持在一条线上,稳定性表现良好,在大于5 MHz 情况下,频率响应才开始出现明显的变化,而且其带宽也满足系统的要求。图6 所示的实验测得的不同频率下电流源的输出阻抗,其中横坐标是输出频率,纵坐标是恒流源输出阻抗。
由图表明,由THS4201 构建的恒流源在1 MHz范围内有良好的输出特性,在600 kHz 前保持在190 kΩ,在800 kHz 时的输出阻抗达到约180 kΩ,满足多频EIT 复阻抗检测对激励源输出阻抗的要求,在一定程度上保证了系统精度。
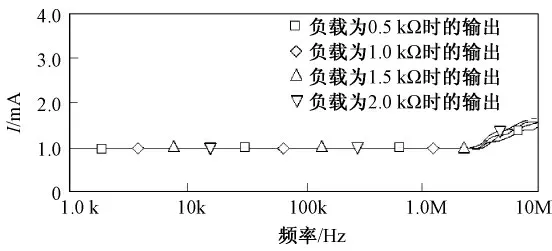
图5 在不同负载下输出电流幅值的频率响应Fig.5 Frequency response of the amplitude of the output current at different loads
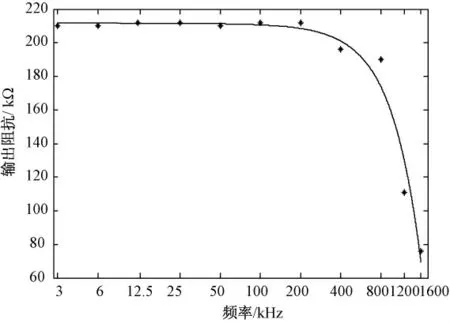
图6 在不同频率下电流源的输出阻抗Fig. 6 The output impedance of the current source at different frequencies
2.2 解调性能结果
为评价正交序列解调器的工作性能和解调精度,假设待解调电压信号的幅度A 为2,相移为π/6,将经A/D 采样后的256 个离散量化数据值存储于ROM 中,设A/D 工作频率为20 MHz,即采样周期Ts=0.05 μs。取A/D 采样10 个激励周期的数据计算一个Q 和I 值,则改变DDS 的频率控制字K可获得不同的N 值,如表1 所示。从表中可以看出,所得到的幅度和相位均存在相对误差。这种误差主要来源于ADC 的采样量化误差和对乘累加的高位截取。在K = 512 时,幅度的相对误差为7.19%,用分贝表示为0.6 dB,相位的相对误差为5.34%,误差范围在1.6°;在K =64 时,幅度的相对误差为1.13%,用分贝表示为0.1 dB,相位的相对误差为1.03%,误差范围在0.3°。在取合适的频率控制字K = 256 时,系统能做到的幅度误差为3.46%,即0.3 dB,相位的相对误差2.29%,误差范围小于1°。在保持待解调信号幅度和相位的值不变的情况下,发现解调输出误差与N 值有关。固定计算一个I 或Q 值所需的ADC 激励周期数,当频率控制字K 增大时,电路计算所得的正交解调实部和虚部的相对误差也随之增大。这是因为增加K 增大了正交解调输出的I 和Q 的误差,进而也增大了所求取的幅度值和相位值的误差。这预示着在实际EIT 检测中,高频激励下应增加N 值以保证一定的解调输出误差,即应采集更多的点计算一个幅度值或相位值。

表1 不同N 值及对应计算所得的I 和Q 值Tab.1 The different N value and the I and Q values of the corresponding calculation
2.3 盐水槽实验结果
测量通道的一致性直接影响系统的性能,通过检验电位差分布测试通道一致性。采用16 电极,相邻激励相邻测量模式进行测量,将一对电极作为激励可以得到13 个有效数据,然后切换到下一对电极同样得到13 个有效数据,依次类推最后得到16 组共208 个测量电压数据,将测量电压数据进行编号,用横坐标来表示,纵坐标表示为检测到的电压值,结果如图7 所示. 从图中可以看出测量电极的电位差以激励电极为中心向两侧呈U 形分布,曲线顶部的个别数据存在误差较大,但是U 形曲线的底部数据分布合理,表明所测试的研究平台性能较好,可满足EIT 测量要求。
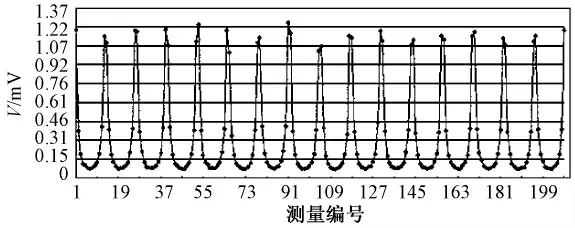
图7 通道一致性测试的U 形曲线Fig. 7 U-shaped curve of the channel conformance testing
对环氧树脂棒进行成像,其在盐水槽中所处的位置和相应的成像结果如图8 所示。图8 中(a)是对环氧树脂棒在中间位置的成像,(b)是对环氧树脂棒在中心位置与盐水槽边缘之间的中心点所成的像。根据以上的成像结果,可以看出当成像目标位于中心位置时,电流密度小,灵敏度降低,到位置2 时电流密度变大,所成像的效果比位置1 的成像效果好。

图8 成像结果(上为实物,下为成像)。(a)位置1;(b)位置2Fig.8 Imaging experimental results(The above picture shows the object,the below one shows the corresponding image). (a)Position one;(b)Position two
3 讨论
我们知道,对应不同频率放大器的输出阻抗等参数是变化的,即使是根据参数表达式计算也同样是困难的,并且从测试的结果而言其输出阻抗都大于真实阻抗,特别是随着频率的升高更加明显,而且真实的输出阻抗都随着频率的增加而减小,当频率过大时将出现严重的失真,原因包括电流源输出端的相位改变和寄生电容对负载的影响。因此在设计电路时可以考虑对输出端的相位进行补偿来减小其对负载的影响,而减小寄生电容的方法有复阻抗变换器(NIC)、广义阻抗变换器(GIC)和变压隔离器,将Howland 电路与NIC 或GIC 结合来减少寄生电容对负载的影响,但是必须对每一个频率进行标定,这也限制了其在多频EIT 中的应用。
对于本实验采用的解调方法,相位抖动和同步延时都是造成解调器相位误差的原因,为了消除这种误差,可以通过选择合适的相位增量和修改线性表深度来消除。选择相位增量要尽量选能与线性表深度整除的频点,选择相位深度时既要保证输出的波形有较小的失真,又要保证最大能输出的频率数不会减少。为了消除同步延时,可以设计成激励源向D/A 变换输出数据的同时从A/D 变换器件上读取输入的调制数据,从而实现同步采样。
系统能够对单个目标物体可以实现较准确的定位,但是从图像整体来看,灵敏度依然较低,这与激励源的稳定性、U 形曲线顶部数据的一致性等因素有关。测量通道的一致性直接影响到系统的共模抑制比和测量精度,在研究外进行的通道一致性测试中,测量电极的电位差以激励电极为中心向两侧呈U 形分布,曲线顶部的个别数据存在误差较大,是造成灵敏度较低的原因之一。改进措施包括减少电极间信号的耦合及噪声敏感性,通常可以采用高质量的屏蔽线、缩短引线长度、增加屏蔽驱动电路及优化电路布线等方法。
本研究还需继续改进,更加完善,进一步的研究工作包括:1、提高成像速度,缩短成像周期。由于本实验平台只是进行一些实验的研究,没有真正用于临床,故对于成像速度要求一般,可以在以后的工作中在提高成像速度方面作进一步研究,主要包括两个方面:一个是采集和处理数据的速度,这由系统的硬件决定,所以在以后可以考虑采用采样速率更快的转换器和实现系统的多通道采集;二是成像算法同样影响成像速度,因此以后可以在算法上作更深一步的研究。2、研究性能更好的恒流源,使之有更宽的工作频带,可在较高的激励频段保持足够的输出阻抗,但是随着激励频率的升高,对后续信号处理电路,包括隔离、放大、解调及滤波电路的设计带来挑战。
4 结论
本研究基于实验室相关的方法学研究成果和技术储备,研究了基于FPGA 的数字化EIT 测量系统,完成了DDS 数字电流源和数字解调。针对恒流源的稳定性和输出阻抗问题,采用改进的Howland电路由THS4021 芯片构建恒流源激励源,在6.1 ~390.6 kHz 的范围内输出阻抗在200 kΩ,并保证了其稳定性。最后通过数字正交解调方法获取被测阻抗信号的实部和虚部信息,系统能做到的幅度误差为0.3 dB,相位误差小于1°,并进行误差分析,结果显示解调输出误差与采样点数有关。最后进行盐水槽成像实验,虽然成像误差较大,但是对单个目标物体能够实现较为精确的定位。
[1] 任超世. 生物电阻抗测量技术[J]. 中国医疗器械信息,2004,10(1):21 -25.
[2] Saulnier GJ,Blue RS,Newell JC,et al. Electrical Impedance Tomography[J]. IEEE Signal Processing Magazine,2001,18(6):31 -43.
[3] Boone K,Barber D. Review:Imaging with electricity:Report of the European concerted action on impedance tomography [J].Journal of Medical Engineering & Technology,1997,21(6):201 -232.
[4] Halter RJ,Hartov A,Paulsen KD. A broadband high frequency electrical impedance tomography system for breast imaging[J].IEEE Trans Biomed Eng,2008,55(2):650 -659.
[5] Ren Chaoshi,Li Zhangyong,Wang Wei. Noninvasive gastric motility measurement and evaluation by bioimpedance [J].Journal of Clinical Rehabilitative Tissue Engineering Research,2010,14(9):1653 -1657.
[6] Brown BH. Cardiac and respiratory related electrical impedance changes in the human thorax. IEEE Trans Biomed Eng,1994,41(8):729 -733
[7] N. Liu,Saulnier GJ,Newell JC. A multichannel synthesizer and voltmeter for electrical impedance tomography. Proceedings of the 25Th Annual International Conference of the IEEE Engineering in Medicine and Biology Society,2003,4:3110 -3113.
[8] 刘延勇,董秀珍,尤富生,等. 两种基于直接数字合成技术的阻抗激励源的对比研究[J]. 第四军医大学学报,2005,26(17):1618 -1620.
[9] 王 超,王化祥. 电阻抗断层图像重建算法研究- 预迭代算法提出[J]. 信号处理,2002,18(6):547 -555.
[10] 王 研,沙 洪,任超世. 电阻抗断层成像线电极的仿真研究[J]. 生物医学工程学杂志,2007,24 (5):986 -989.
[11] Wang Huaxiang,Cui Ziqiang. FPGA based signal generator in EIT system[J]. Chinese Journal Of Electron Devices,2007,30(1):90 -96.
[12] Ho KC,Chan YT,Inkol R. A digital quatrature demodulation system [J]. IEEE Transactions on Aerospace and Electronic Systems,1996,32(4):1218 -1227.
[13] Zhao Fei,Guo Wei. Two kinds of dds implementing with FPGA[J]. Modern Electronics Technique,2010,29(1):204 -206.
[14] 秦玲,张良,赖青贵,等. 基于功率运算放大器的恒流源技术研究[J]. 通信电源技术,2007,24(1):43 -46.
[15] 杨彬,党瑞荣,杨灏. 一种高精度波形发生器的设计及实现[J]. 石油仪器,2007,21(1):11 -13.
[16] 吴右,沙洪,任超世. 基于DSP Builder 的EIT 正交序列解调方法与电路设计[J]. 国际生物医学工程杂志,2009,32(5):276 -279.
[17] Tong IO,Eung JW,David H. Multi-frequency EIT system with radially symmetric architecture[J]. Phys Meas,2007,28(7):183 -196.
