基于复杂度熵特征融合的高压力人群情感状态评估
2013-03-10李红红李长吾燕山大学生物医学工程研究所秦皇岛066004
李 昕 李红红 李长吾(燕山大学 生物医学工程研究所,秦皇岛066004)
2(河北省测试计量技术及仪器重点实验室,秦皇岛066004)
3(大连工业大学信息科学与工程学院,大连116000)
引言
目前,压力评估的研究主要集中在3 个方面:一是通过调查对某一行业、群体的心理压力源进行识别,并谈论心理压力的应对方式;二是研究心理压力中具体的工作压力、择偶压力、养老压力、婚姻和家庭生活压力等;三是在心理学、管理学等学科理论的基础上,以心理压力源的某一变量为研究对象,剖析该变量与其他变量的关系[1]。实时状态下的压力评估研究还不多见,如果能对高压力人群的情绪及压力状态进行及时准确的评估与适度调节,他们的情感及生活状态会给予社会一个良性的反馈;反之,可能引发各种心理、行为问题,轻则影响学习和生活,重则引发抑郁等严重心理疾病甚至发生恶性事件,给个人和社会带来很多危害。
自然状态下的压力研究有助于分析人们的情绪化行为,同时能够对个体的压力水平进行一个较为客观的评估。基于生理参数来评估压力,对于主体来说不适感最小,并且能够准确地反映情绪状态,是目前公认的较好的压力评估方法。
Healey 等通过连续记录通往波士顿市中心、在固定路段上行驶的汽车司机的心电、肌电、皮肤电传导和呼吸信号4 种生理信号,基于线性判别分析,证明了生理参数对预测心理压力具有很高的精确度[2]。Mokhayeri 等证明了压力评估的必要性与可行性[3]。德国Augsburg 大学采用一款传统的游戏“俄罗斯方块”作为压力源,采集了1 名被试者的呼吸信号和肌电信号,基于LDA 和Fisher 判别对结果进行分析,平均识别率达80% 以上[4]。Gaggioli 等设计了一种用于评估压力状态的简单无线装置,基于自回归建模、人工神经网络、模糊逻辑模型的方法,通过分析心电信号及动作特征来实现自动、连续检测,并自动识别日常活动中的压力状态[5]。
Hernandez 等以9 名话务中心工作人员作为实验对象,研究了自动识别压力/非压力反应中的个体差异问题,即修改支持向量机中的损失函数参数,并从相似的皮肤电变化人群中抽取训练样本。结果表明:同一人但在不同时间的情况下,训练和测试得到的正确率是78.3%;而对于支持向量机的修改方案,在不同参与者间进行训练和测试得到的正确率是73.41%[6]。
脑电信号是一种产生机理复杂的非平稳随机信号,其数据的采集过程复杂且容易受外界环境以及其他生理信号的干扰,国内外将脑电信号用于压力识别的研究中与其他生理信号相比还不多见。
但是,同其他生理信号相比,脑电信号含有丰富的情感信息。充分挖掘脑电压力的情感特征,将有助于更好地实现压力情感的分析与评估。笔者以“切水果”游戏作为压力源,采集了8 名被试者的92 组脑电信号;基于复杂度与熵理论相结合的方法,实现脑电信号的特征提取与融合;基于改进的SVM 分类器,实现了基于脑电信号的情感压力状态评估。
2 基于复杂度、熵的脑电信号特征提取
脑电信号直接反映神经元电话动,蕴含丰富的情感信息,在理论研究和临床应用上都有着重要意义。如何有效地提取脑电特征参数,一直是研究的热点。复杂度、近似熵、小波熵提供了一种客观、定量地描述事物复杂程度的方法,可从不同的角度研究脑电信号的非线性动力学特征。本研究基于Kc复杂度、近似熵、小波熵理论,分析在压力状态下脑电信号的复杂程度与能量分布,并以此评估压力情感状态。
2.1 基于Kc 复杂度的脑电信号特征提取
Kc复杂度又称算法复杂度或L-Z 复杂度,是最经典的复杂度定义,应用非常广泛。Kc复杂度反映了时间序列的随机程度,其值介于0 ~1 之间。如果时间序列是周期性的,那么Kc就会随时间序列的增加而趋向于0;如果时间序列是随机的,则Kc趋向于1。这表明,随机信号序列最复杂,周期信号最简单。算法流程[7]如图1 所示,其中S 和Q 分别代表两个字符串,SQ 表示把S、Q 两个字符串拼接的总字符串。SQw 表示SQ 中最后一个字符删去所得到的字符串。令V(SQw)表示SQw 所有不同子串的集合,C 为X 序列的复杂度计数。
初始化C =l,S = s1,Q = s2,此时SQw = s1,假定S = s1s2…sr,Q = sr+1,如果Q ∈V(SQw)则表示sr+1是s1s2…sr的一个子串,此时S 不变,将Q 更新为Q =sr+1sr+2,再判断Q 是否属于SQw。重复上述操作,直到Q ∉V(SQw)。此时Q = sr+1sr+2…sr+i,C= C + 1,S 更新为s1s2…sr+1sr+2…sr+i,Q = sr+i-1。重复以上步骤,直到Q 到最后一位,s1,s2,…,sN分成了C 个子串。
Lempel 等指出[8],几乎所有属于[0,1]区间的x 对应的二进制分解都会指向一个函数b(n) =n/lg(n),所以是随机序列的渐进行为对C 进行归一化处理,c =/b(n)。此时c 称为Kolmogorov 复杂度。
2.2 基于熵理论的脑电信号特征提取
2.2.1 近似熵
1991 年,Pincus 提出近似熵(approximate entropy,ApEn)理论[9]。近似熵是一种度量时间序列复杂性和统计量化的规则,是一种不需要进行粗粒化的脑电复杂性测度分析方法。该算法用一个非负数表示时间序列的复杂性,越复杂的时间序列对应的近似熵越大[10-12]。该算法只需很短的时间序列(约1 000 个数据点),就足以估算出可靠的ApEn 值,并不企图完全重构吸引子,而是用一种有效的统计方式——边缘概率密度的分布来区分各种过程,因此特别适用于生物电这类极其不稳定信号的分析。
近似熵的具体算法[7]如下:设原始数据为u(1),u(2),…,u(n),共n 点。对于u,按顺序将其组成一个m 维的向量集X(i),即从第i 个点开始连续的m 个u 值,其中参数m 是比较序列的长度,即窗口长度,也叫嵌入维数。
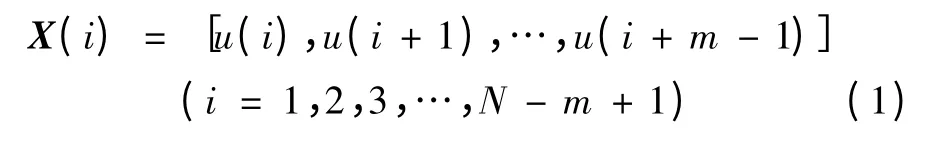
1)计算向量X(i)与其余向量X(j)之间的距离d(X(i),X(j)),并将其最大值定义为最大反应成分距离,即
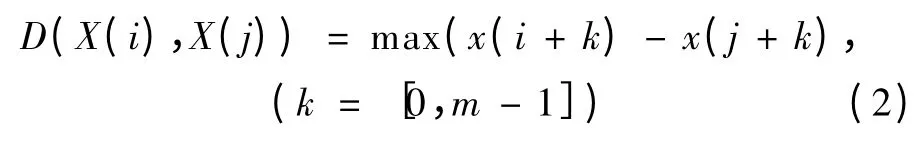
其中,i,j = 1,2,…,N - m + 1
2)定义一个阈值r(r >0),对于每一个i≤N-m+l 值,记录满足条件d(X(i),X(j))< r 的个数。这个值与总数N-m +l 的比值定义为
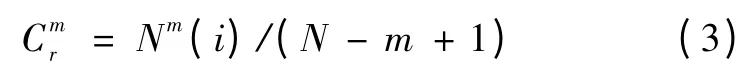
3)对每一个可能的i 值,计算Cmr 的对数,求这些对数的平均值,定义为φm(r),即
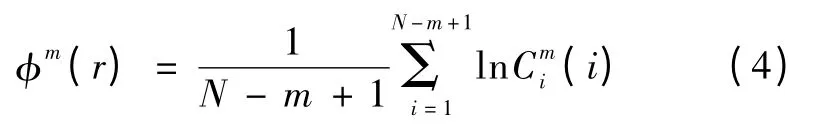
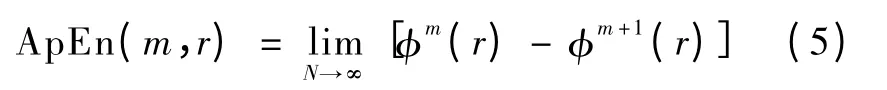
该极限存在,且极值为1。因此,ApEn 表示向量集随着m 增大产生新模式的概率,产生新模式的概率越大,ApEn 值就越大,时间序列的复杂度越大。实际上,N 不可能取无穷大,所以通常只能在N足够大的时候,对ApEn 进行估计,同时,ApEn 的值还依赖于m 和r。
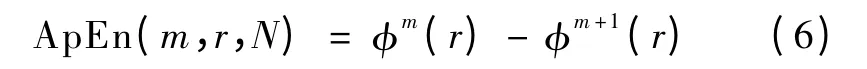
根据经验,Pincus 建议m 取2,r 取0.1 ~0.2 倍原始数据的标准差。从而只需用很短的时间序列(约1000 个数据点)就可以估算出可靠的ApEn 值。
2.2.2 小波熵
根据小波变换的框架理论,当小波基函数是一组正交基函数时,小波变换具有能量守恒的性质,小波熵可以通过小波系数求得[13]。
离散时间信号f(t),经过J 层离散小波变换分解后,低频近似分量系数为AJ,高频细节系数 为Dj,其中j = 1,2,…,J。单一尺度下的小波能量为该尺度下小波系数的平方和,总的小波能量为
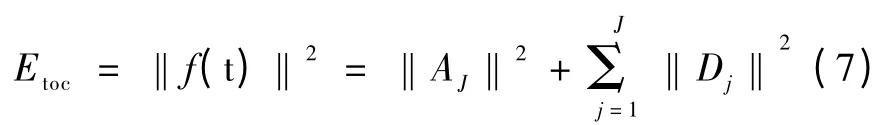
为了统一,将AJ表示为DJ+1则总能量为
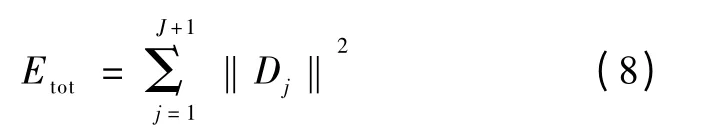
相对小波能量为
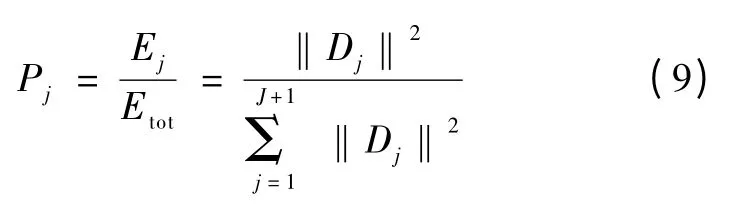
小波变换具有良好的时频局部化性能,根据Shannon 熵理论和相对小波能量的定义,小波熵(wavelet entropy ,WE)的定义为
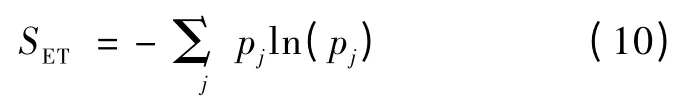
式(10)反映了整个信号的不确定性和复杂程度[14]。
小波变换反映了信号在时频域中能量的分布状况,不同信号在时频分布上的差异表现为不同子块时频区间能量分布的差异。小波熵理论是基于小波分析方法建立起类似信息熵的理论,能够对时频域上能量分布特性进行定量描述。
基于以上算法,提取融合Kc复杂度因子,近似熵、小波熵3 类情感特征参数,以遗传算法改进的支持向量机作为融合分类器,比较单一情感特征与融合情感特征的压力情感状态识别效果。
3 基于支持向量机的模式分类
支持向量机(SVM)由于较好地解决了小样本、非线性及高维数、局部极小值点等实际问题,已逐渐成为解决模式分类问题的首选工具。本研究基于改进支持向量机融合3 类不同域描述的情感特征参数,解决基于脑电信号的压力情感状态评价分类问题。
选用C-SVC 模型以及RBF 核函数,基于遗传算法的参数寻优与分类流程见图2。首先选择实值编码策略,设置种群大小取20 代,最大进化代数设定为100,交叉和变异概率分别设为0.4 和0.01。通过GA 寻找最优惩罚系数c 和核参数g,设定参数并训练分类器。将预处理过的脑电信号基于小波变换提取β 波,然后将提取的Kc复杂度、小波熵、近似熵3 种特征融合,送入训练好的分类器中进行分类评估。

图2 小波包特征提取并由经GA 优化的SVM 分类的算法流程Fig.2 Flow chart of the SVM improved by GA classification with the wavelet packet-based feature extraction
4 实验与数据采集
心理研究表明,当人在规定时间内完成指定任务时会产生心理压力,而人在情绪紧张或感到压力时脑电的β 波明显。本实验记录被试者在玩“切水果”游戏时的脑电信号,研究其β 波的变化规律。
4.1 实验设备和数据采集
脑电信号采集通过Neuroscan 记录系统(见图3)完成。记录电极使用的是该公司的Quick-cap32导电极帽,Ag-AgCl 杯状电极。电极安放位置按照10 -20 国际电极系统放置法放置,电极的接触阻抗均小于10 kΩ。信号采样率为1 000 Hz,信号通过0~30 Hz 的低通滤波。
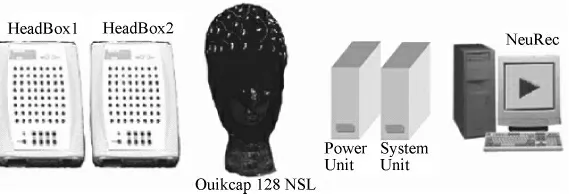
图3 Neuroscan 记录系统Fig.3 Neuroscan Recording System
脑电数据的采集来自8 例受试者(4 例男性,4例女性)。受试者均为燕山大学的在读研究生,年龄23 ~25 岁,右利手。受试者的脑电采集来自两种状态,睁眼休息和游戏。实验在一个隔音、隔光的屏蔽室内进行,受试者坐在一个舒适的靠椅上进行脑电纪录。在记录脑电时,关闭屏蔽室内的灯光,保持周围安静。
4.2 实验流程
在实验前,先让被试者休息几分钟,让其放松平静下来,生理特征达到平常状态。主动与被试者沟通,让他们了解测试流程,缓解紧张和好奇的情绪。
在实验过程中,首先让受试者静息5 min(过程中注意闭上眼睛,不能左右转动眼珠,不能睁眼,不能睡觉,不能思考问题,周围要保持安静),然后睁眼静息2 min 后开始切水果游戏,游戏持续60 s,记录下这个过程中的眼动和脑电数据。要求每名受试者实验时重复上述过程3 次。
在记录前,实验人员告知受试者睁眼还是闭眼静息,待脑电波平稳后开始记录脑电,在每种状态下记录约2 min 的脑电信号,保存信号以进行下一步的分析。采集过程中的原始数据记录见图4。
5 脑电信号预处理
5.1 脑电信号的特征选择
脑电信号是一种产生机理相当复杂的非平稳随机信号,主要由各种节律性电活动组成,根据一般脑电节律的频率分段标准[7],将脑电信号分为α波、β 波、θ 波、σ 波4 种基本节律。α 波主要是在闭眼时较为明显,在睁眼时会减弱或消失,而实验设计是游戏实验,整个实验过程被试都是睁眼状态,因此α 波不作为分析的主要信息。θ 波和σ 波主要是正常儿童和婴儿的主要脑电活动,而本次的实验对像为23 ~25 岁的在读研究生,因此也不作为实验的分析节律。β 波由于不受睁眼和闭眼的影响,且在大脑皮层兴奋状态时表现明显,因此本次实验主要是提取脑电信号中的β 波来用于压力评估与分析。
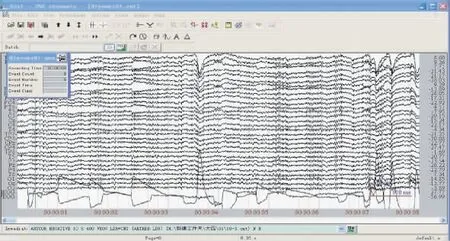
图4 原始数据采集Fig.4 Raw data acquisition
5.2 基于小波包变换的β 波提取
所用的数据是实验室自采的数据,共有8 个被试者的92 组原始数据,其中44 个静息样本,48 个游戏样本。
首先将采集的. cnt 格式脑电数据用Neuroscan自带的分析软件进行去除眼动的处理。使用Matlab中eeglab 工具箱对其进行重采样(重采样频率为128 Hz),基于ICA 方法对数据进行去噪处理。截取9 s 不同状态下的平稳脑电信号,共1 152个数据点,使数据长度一致,以便下一步分析。
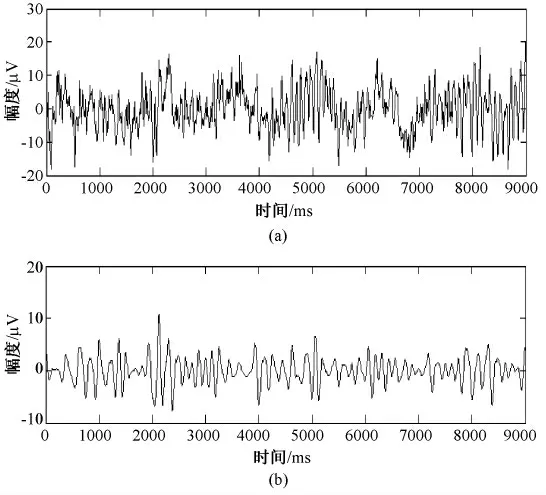
图5 脑电图。(a)原始脑电;(b)经小波包重构的β 波Fig.5 EEG. (a)The original EEG;(b)The extracted β wave based on the wavelet packet.
如图5 所示,(a)为采集的原始脑电信号,(b)为采用daubechies 小波对脑电信号进行6 层分解,并将β 波所包含的分解节点进行重构。
6 结果
以FC3 电极为例,依据上述3 种特征提取方法,提取不同的特征向量并组合,送入SVM 分类器,所得结果为:最大分类正确率为94.12%,平均分类正确率为82.06%。
图6 所示为分类器寻优时的适应度曲线,偏上的实点线是最佳适应度曲线,偏下的圆圈线是过程中的平均适应度曲线。此次寻优所得最优的惩罚参数c =2.18,核参数g =0.88,寻优时运用n 倍交叉验证时所得分类正确率为78.34%。
训练集与测试集样本以50∶42 的比例训练分类器,每组样本测试循环20 次,实验结果见表1。由于在额区、颞区、中央区的β 活动最为明显。为了选取最能体现实验结果的电极,选取上述3 区中的8 个电极(C3,C4,F3,F4,FC3,FC4,FP1,FP2)进行数据处理及分析,将平均分类准确率最高的3 种特征融合的结果进行对比,如表2 所示。
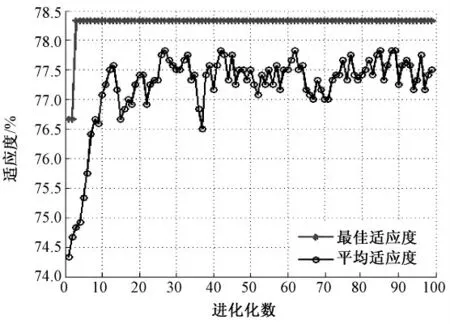
图6 GA 参数寻优方法寻优时的适应度曲线Fig. 6 The fitness curve using GA when searching c and g.
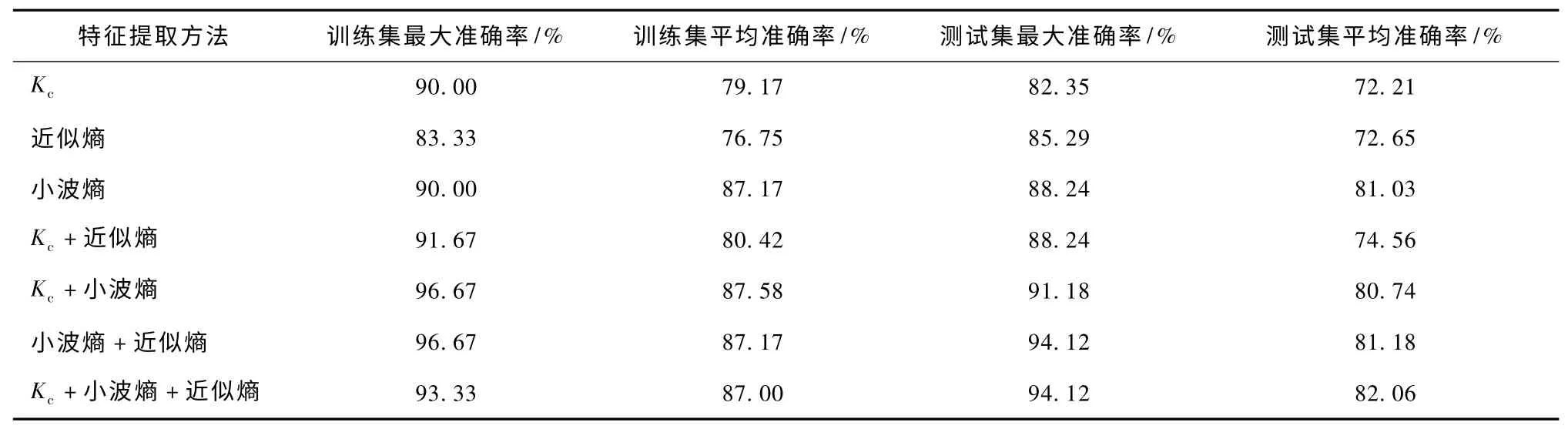
表1 不同特征提取方法的分类结果比较Tab.1 Comparison of the classification results of the different feature extraction methods
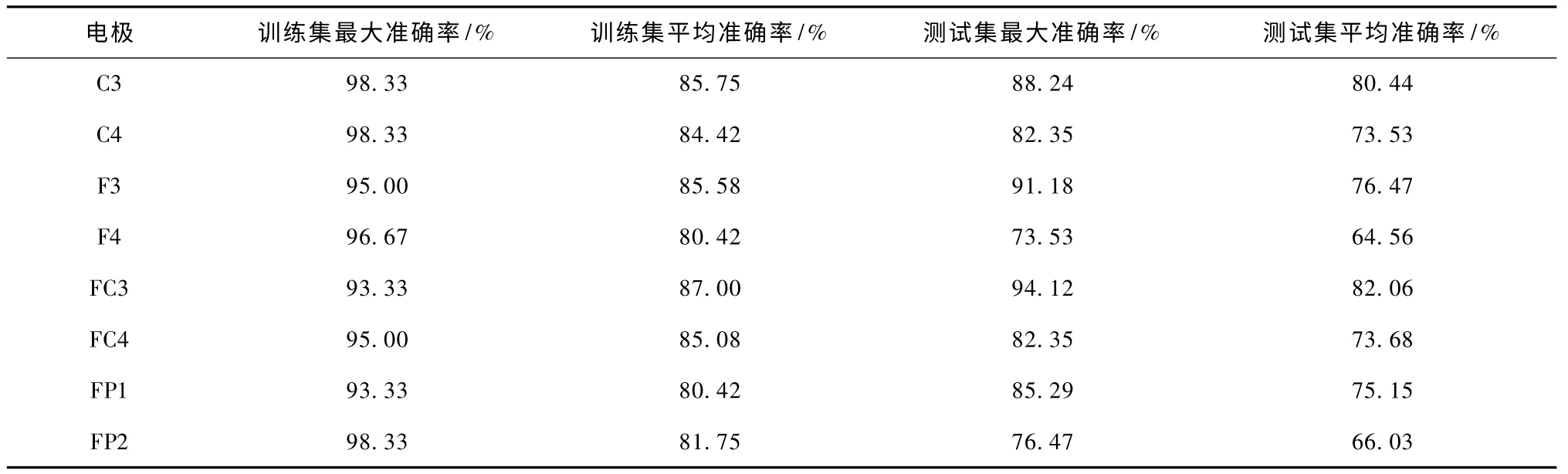
表2 不同电极3 种特征融合的分类结果比较Tab.2 Comparison of the classification results of the different electrodes for three features fusion
7 讨论
采用3 种算法的不同组合方式,比较SVM 分类结果。由表1 可知,在对脑电信号进行特征提取并单独使用一种算法时,小波熵的分类识别率最大为88.24%,平均识别率最大为81.03%。在两两组合的特征选择中,最高的是近似熵和小波熵组合的识别率,为94.12%,平均识别率最大值为81.18%;融合3 类特征中,最大识别率为94.12%,平均识别率82.06%。
在3 种算法(Kc复杂度、小波熵、近似熵)中,小波熵平均识别率高于 Kc复杂度平均识别率8.82%,这与脑电信号的特征提取算法的特性有关。β 波在大脑皮层兴奋状态时表现明显,Kc复杂度这种过分的粗粒化可能改变了信号的动力学特性,所以识别率不是很高;小波熵理论是基于小波分析方法而建立的类似信息熵的理论,能够对时频域上的能量分布特性进行定量描述,在游戏和静息两种状态下,脑电信号的复杂度前者高于后者,识别率相对较高。近似熵是对时间序列的复杂度进行的分析,其变换幅度要好于复杂度,需要的数据长度短于复杂度,但运算速度要比Kc复杂度慢。综上所述,三者结合应为比较理想的特征组合。实验结果也说明,融合3 类情感特征参数,测试识别率较高。
由表2 可知,奇数电极比对应偶数电极的分类准确率高,也就是脑的左半球相对右半球来说,对压力的感受比较敏感;相对其他电极,FC3、C3 电极的分类准确率较高。
人的左脑与右脑形状相同,功能却大不一样。人的左脑侧重于理性思维,善于推理,逻辑性强,而右脑侧重于感性思维,善于创新,跳跃性强。
笔者所研究对象为β 波,其频率为13.28 ~30.47 Hz。在额、颞、中央区活动最为明显。在睁眼视物、情绪紧张、焦虑不安、惊疑恐惧或服用安定等药物时,β 波活动急剧增多。同时,β 波的活动也与人的某些心理品质有关。β 节律优势的人常表现为精神紧张、情绪不稳,善于独立地执行任务;长于抽象思维,喜欢依靠“推理"解决问题,还表现出持久力差、易于疲劳的特点。所以当面对压力时,β 波表现明显。
由于功能不同,左右脑在面对压力时产生的β波不应相同,即左右脑对压力的感受程度不同,表2的结果验证了左脑比右脑对压力感受更为敏感的结论。
FC3、C3 电极在中央区,属于左半球,分类准确率较高符合上述推理。而理论上额区的FP1、F3 应高于其他电极,但可能是电极在额区贴的不够服帖,所以效果不如FC3、C3。
8 结论
本研究以脑电数据为对象,采用Kc 复杂度、小波熵、近似熵算法,提取脑电数据压力情感特征,基于改进支持向量机融合压力情感特征,实现压力情感状态的自动评估。
实验结果表明,基于此特征提取融合算法,压力情感状态最高识别率为94.12%,平均识别率为82.06%。基于该特征提取算法,实现压力人群情感状态评估是可行的。
同时,比较了不同脑区对于压力情感的敏感程度。结果表明,脑的左半球相对右半球来说,对压力的感受敏感;相对其他电极,FC3、C3 电极的分类准确率较高。
希望通过此项工作,帮助人们有针对性地采取相应措施来缓解压力,恢复身心健康。
[1] Milette K,Roseman M,Thombs BD. Transparency of outcome reporting and trial registration of randomized controlled trials in top psychosomatic and behavioral health journals:A systematic review Original Research Article[J]. Journal of Psychosomatic Research,2011,70 (3):205 -217.
[2] Healey JA, Picard RW. Detecting stress during real-world driving tasks using physiological sensors [J]. IEEE Intelligent Transportation Systems Society,2005,6(2):156 -166.
[3] Mokhayeri F,Akbarzadeh TMR. Mental stress detection based on soft computing techniques[C]// IEEE International Conference on Bioinformatics and Biomedicine. Atlanta:IEEE,2011:430 -433.
[4] Wagner J. Augsburg Biosignal Toolbox (AuBT)User Guide[OL]. http://emotion-research. net,2012 - 10 - 8/2012 - 12-5.
[5] Gaggioli AG,Pioggia G,Tartarisco G,et al. A system for automatic detection of momentary stress in naturalistic settings[C]// Wiederhold BK,Riva G ,eds. Studies in Health Technology & Informatics. Biussels:IOS Press,2012:182 -186.
[6] Hernandez J, Morris RR, Picard RW. Call center stress recognition with person-specific models [C] // Mello SD,Graesser A,eds. Affective Computing and Intelligent Interaction,Berlin:Springer-Verlag,2011,125 -134.
[7] 刘秉正,彭建华. 非线性动力学[M]. 北京,高等教育出版社2004.
[8] LempelA,Ziv J.On the complexity of Finite sequence[J]. IEEE TransInf Thcory,1976,IT22:75 -81.
[9] Pincus SM. Approximate entropy as a measure of system complexity[J]. Proceedings of the National Academy of Science.1991,88(6):2297 -2301.
[10] Bruhn J,Hoeift A,Ropcke H,et al. Approximate entropy as an electroencephalographic measure of anesthetic drug effect during desflurane anesthesia[J]. Anesthesiology,2000,92(3):715 -726.
[11] 华光,任维,刘钢,等. 近似熵及其在心率变异分析中的应用[J].航天医学与医学工程,2000,13(6):417 -421.
[12] Ocak H. Automatic detection of epileptic seizures in EEG using discrete wavelet transform and approximate entropy[J]. Export Systems with Applications,2009,36(2):2027 -2036.
[13] 李建勋,柯熙政,丁德强. 一种基于小波熵的时间尺度算法[J].天文学报,2007,48(1):84 -92.
[14] Rosso OA,Blanco S,Yordanova J,et al. Wavelet entropy:a new tool for analysis of short duration brain electrical signals[J]. Neurosci Meth,2001,105(1):65 -75.
