基于多特征的颅内脑电癫痫检测方法

陈爽爽 周卫东 袁 琦 袁莎莎 栗学丽

(山东大学信息科学与工程学院，济南 250100)

引言

癫痫是一种脑部疾患，以脑部神经元反复突然过度放电所致的间歇性中枢神经系统功能失调为特征。长程脑电(EEG)检查是临床上常用的癫痫检查手段，对癫痫脑电图的分析有助于医生发现病人的病灶并进行相应的治疗，该工作目前主要由医疗工作者根据脑电图通过视觉检测来完成。但人工观察和检测长程EEG 是一项复杂而又耗时的工作，且往往要通过经验来做出判断。因此，脑电图的自动检测与分类就越发显得迫切与重要［1］。

自20 世纪60 年代起，自动癫痫检测技术就受到了广泛的关注和研究，这一领域的众多学者提出了多种自动检测的方法［1-2］。由于癫痫发作时，大脑会产生尖波、棘波、慢波、尖慢综合波、棘慢综合波等多种形式的波形，且癫痫发作期波形变化比间歇期剧烈，众多学者利用脑电波的时频特性来进行特征提取，通过模拟医务工作者视觉评判的过程，达到自动检测癫痫发作的目的［3］。EEG 波形的时频特性主要包括:1)相对能量［1］，指信号经小波分层后某层的能量和所有层的能量和之比;2)拟态法的特征［4］，提取波形的部分参数进行识别，此种方法应用的较为广泛;3)模板匹配［5］，提前选取典型癫痫脑电波形作为模板，将检出的波形与癫痫脑电模板进行匹配识别。无论采用何种方法，通常要求棘波自动检测系统有较高的正确率，较低的漏检率和误检率。

与皮层脑电不同，颅内脑电包含较少的干扰，但是却包含了种类较多、频率较高的癫痫样放电成分，这给癫痫自动检测增加了难度［6］。本研究提出一种采用多特征的颅内EEG 癫痫检测方法。依靠发作期EEG 多个特征的统计概率，通过贝叶斯概率公式计算得出患者癫痫发作的可能性，再通过设定阈值的方法，达到一个较为满意的灵敏度和误检率。在癫痫检测的过程中，采用微分方差、相对能量、波动指数多种特征相结合，从而提高了系统的检测性能。

1 脑电信号及预处理

1.1 数据选择

实验所使用数据来自德国Freiburg 医学院癫痫研究中心，均为对难治愈型癫痫患者在术前监护中采集到的颅内脑电数据［7］。数据由21 例癫痫患者的6 个导联脑电数据组成，且每一位患者均有3 个导联处于发作病灶区，3 个导联处于非病灶区。共87 次癫痫发作，持续509 h 的发作间期以及持续73 h 的发作前期。每一位患者的脑电记录中至少包括50 min 的发作前期的数据及10 h 以上发作间期的数据。脑电数据由Neurofile NT 数字视频脑电监护仪记录，采样频率为256 Hz，16 位A/D 转换器，且用0.5 ～120 Hz 的带通滤波器对脑电数据进行了滤波处理。

1.2 脑电信号分解

首先对长程脑电数据进行连续分段，每段4 s，共计1 024 个数据点。然后，利用Daubechies-4 小波进行5 层的小波离散变换。经研究表明，癫痫EEG经常发生在3 ～30 Hz 范围内［8］，也就是脑电信号的θ 频段、α 频段和β 频段，所以本次实验中，仅在这3个频段即第3 ～第5 层上进行特征的提取。

1.3 半波处理

数据进行分层后，对每段各层的数据进行半波处理，目的是去除叠加在脑电信号上的小振幅快波。根据Gotman 提出的半波处理的方法［2-3］，首先对预处理后的EEG 数据根据振幅极值趋势进行分段处理;然后，对重新分段的数据按顺序进行重组，组成半波。

2 特征提取

对预处理过后的脑电信号进行特征提取。根据癫痫发作时EEG 时频域的变化，提取微分方差、相对能量和波动指数来量化脑电信号的特征。

2.1 微分方差

微分代表参数变化率，利用微分的这种特性，来判别癫痫波和背景波。由于癫痫波与背景波空间上的相近性，自动癫痫检测时需要将两者分离开。而窗口方差就是一种简单但是有效的分离癫痫波和背景波的方法［7］。微分算子放大了癫痫波并且抑制了背景波，使得利用窗口方差检测癫痫更加有效。

首先，对一段脑电信号S(t)进行微分并进行标准化处理

式中，D'表示微分算子;a 表示标准化常数，实验中，采用a =100 000。然后对所得到的标准化后的微分Y(t)取方差，即得到微分方差

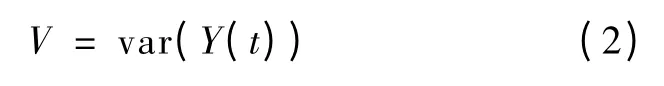
2.2 相对能量

相对能量指的是信号经小波分层后某层的能量和所有层的能量和的比［1］。也就是说，指定层的相对能量本质上是指该层所包含能量与总能量的比值。预处理后第l 层的能量为

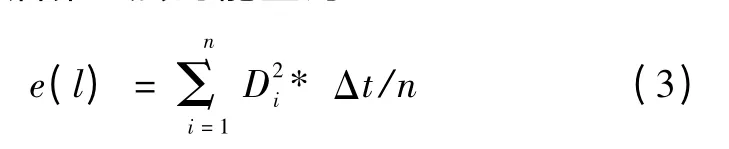
式中，n 代表预处理后每段数据的数量，l 代表小波层的位置，Δt 代表时间间隔。第l 层的相对能量er(l)可以表示为

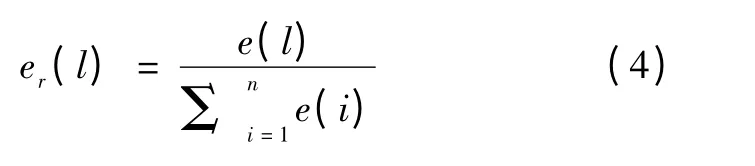
2.3 波动指数

经过长期的临床观察，癫痫发作时脑电信号的波动会比未发作的间歇期剧烈，因此选择波动指数来衡量信号的变化强度［9-10］。波动指数可以表示为

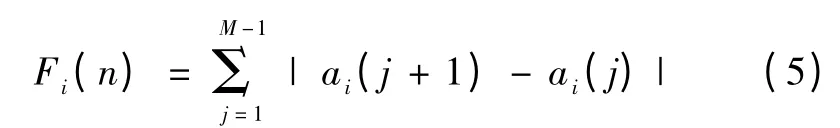
式中，ai为第n 段脑电数据小波变换后第i 层的幅度，M 为信号的长度。

实验表明，癫痫发作期的波动指数通常比未发作的间歇期大，为此使用相对波动指数来衡量脑电信号相对于背景的变化强度，其定义为当前被分析的脑电序列的波动指数与其背景的波动指数之比。背景定义为比当前段EEG 早60 s 的一段长达120 s的脑电信号［6］。因为癫痫发作是一个逐渐变化的过程，选取120 s 是为了保证对波动指数相对稳定的估计。

3 分类器设计

3.1 贝叶斯公式

贝叶斯公式用来描述两个条件概率之间的关系。针对癫痫检测问题，贝叶斯公式可描述为

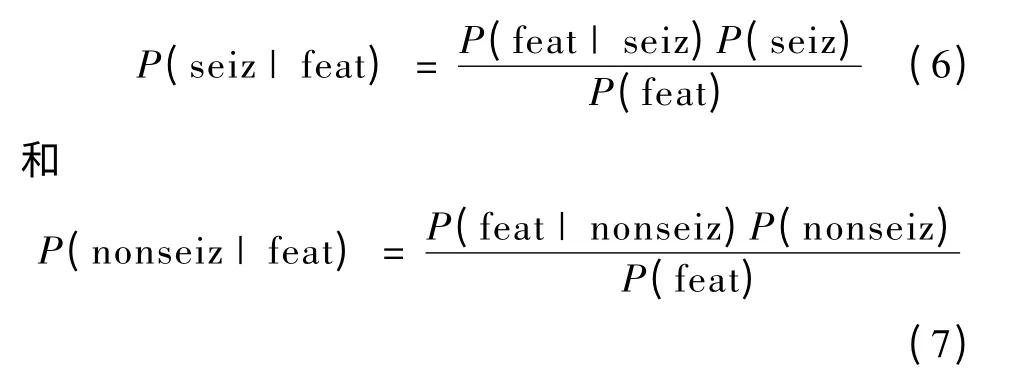
式(6)和式(7)分别为癫痫发作期和间歇期的贝叶斯公式。公式中的各项可以表述为:

1)P(seiz | feat)为某特征下癫痫发作的概率;P(nonseiz | feat)为某特征下无癫痫发作的概率。

2)P(feat | seiz)为癫痫发作状态下某特征出现的概率;P(feat | nonseiz)为癫痫未发作状态下某特征出现的概率。

3)P(feat)为癫痫发作和未发作状态下，某特征出现的概率。

4)P(seiz)为癫痫发作概率;P(nonseiz)为癫痫未发作概率。

这些参数中，后三项均基于训练数据统计得出。癫痫检测时，计算P(seiz | feat)得到判断癫痫发作与否的概率。在本次实验中，利用训练数据得到的先验概率和条件概率来换算出检测癫痫发作的后验概率，并以此作为癫痫是否发作的指示。

3.2 分类过程

预处理后的EEG 数据首先被分解成为发作和未发作两部分从而分别存储。将每段脑电信号(4 s)进行5 层小波分解后计算第3 层、4 层和5 层分量的微分方差、相对能量和波动指数特征，然后将这些特征数据按照数目均分成5 部分，进行排列组合，从而可以得到125 种特征组合。用某一组合所包含的数据段数除以发作期总数据段数，即可得到癫痫发作时该组合特征的概率P(feat|seiz)。同理，用某一组合所包含的数据段数除以无癫痫发作的总数据段数，即可得到无癫痫发作时该组合特征的概率P(feat|nonseiz)。

在单导联中，将第i 层的P(feat|seiz)标记为P(SEIZ_i)，将该导联脑电信号小波分解后第3 层、4 层和5 层分量的PSEIZ_i相加，得到该导联某特征发生的概率和PSEIZ_CHAN;然后将该段脑电各个导联特征发生的概率相加得到PSEIZ_EPCH。采用多种特征相结合，是为了增加癫痫发作检测的准确性。而采用多导联多层概率叠加的方法是为了突出癫痫发作期的特征，从而使自动检测更加准确。同时，注意这里的PSEIZ_EPCH已经不是传统意义上的概率，而是一种由概率求出来的和值。在计算过程中，贝叶斯公式所要用到的P(feat)可由下式得到:

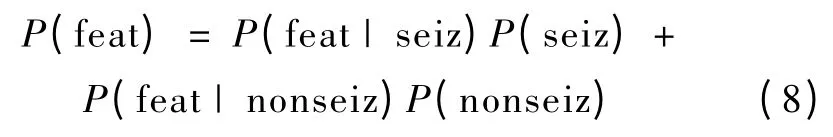
设定一个可调的阈值PTH，当PSEIZ_EPCH大于此阈值，表明出现癫痫发作的可能性较大。通过调节PTH阈值，既可调节癫痫检测的灵敏度、特异性和误检率。

3.3 平滑处理

贝叶斯分类器的输出因存在干扰，并不是一个渐变的过程。因此，在进行判别前，对分类器得出的概率进行平滑处理。使用移动平滑滤波器(MAF)，它的实现方式为

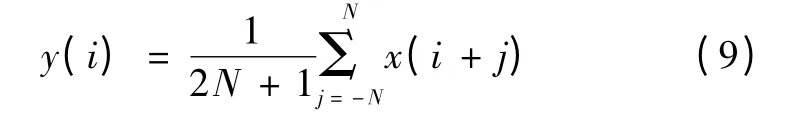
式中，x 表示平滑滤波器的输入变量;y 表示平滑滤波器的输出变量;2N +1 表示平滑滤波器的长度，也就是进行移动平均的数目。

经过对PSEIZ_EPCH平滑滤波，一些偶发的较短时间的干扰得以消除。若平滑后的PSEIZ_EPCH大于阈值PTH，则将该段判定为癫痫发作。反之若小于该阈值，则将该段判为间歇期脑电。阈值PTH可由一经验公式确定:

PTH=训练数据的分类器输出均值-调节系数×分类器输出的方差 (10)调节系数在0 和1 之间，实验中取为0.25。

3.4 验证实验

将所提出的方法应用到临床长程脑电的癫痫波的检测中，实验在AMD Athlon processor 2.71 GHz、1.00 GB 内 存 计 算 机 上 进 行，使 用 Matlab R2011a 软件进行编程。实验中，将脑电数据按时间进行连续分段，每段1 024点，并随机分成两组，一组用来训练，一组用来测试。训练数据包括:254 段癫痫发作脑电和5 400段间歇期脑电。测试数据包括:1 803 段癫痫发作脑电和55 304段间歇期脑电。首先将每段数据进行5 层小波变换。然后，对训练数据进行特征提取，分别求取发作期和间歇期脑电的先验概率和条件概率，得到125 种特征组合的分布概率。测试时，对分段后的测试数据提取特征，得到该段脑电癫痫发作的概率和，从而通过阈值判断，判断该段脑电是否含有癫痫波。

4 实验结果

图1 给出了所用微分方差、相对能量和波动指数等3 种特征在癫痫发作期与间歇期的脑电特征值的对比图，可以看出癫痫脑电的波动指数、相对能量和微分方差要明显高于间歇期脑电。图中100 组特征数据的统计结果见表1，经t 检验，3 种特征癫痫脑电和间歇期脑电之间均具有显著性差异(P ＜0.001)。这些差异表明这3 种特征有助于区分癫痫脑电和间歇期脑电，可用于癫痫脑电的检测。

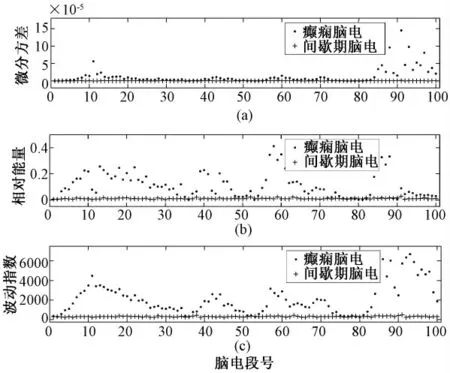
图1 癫痫脑电和间歇期脑电特征对比图。(a)微分方差;(b)相对能量;(c)波动指数。Fig． 1 Feature comparison of seizure and nonseizure EEG epochs． (a)Differential variance;(b)Relative energy;(c)Fluctuation index．

表1 癫痫脑电和间歇期脑电特征统计结果(均值 ± 标准)Tab．1 The statistical results of features of seizure and non-seizure EEG epochs (mean ± SD)

采用灵敏度(sensitivity)、特异性(specificity)和误检率(false detection rate)对提出的颅内自动癫痫检测方法进行评估。灵敏度定义为正确检测的阳性样本占测试样本集中阳性样本总数的比值;特异性定义为正确检测的阴性样本占测试样本集中阴性样本总数的比值;误检率为平均每小时的错误检测次数。癫痫脑电检测的统计结果见表2，对于测试数据可以达到灵敏度94.2 %，特异性为95.6 %，误检率1.16 次/h。

表2 颅内脑电数据癫痫检测结果Tab． 2 Results of epileptic seizure detection from intracranial EEG

目前，已有多种自动检测方法应用于癫痫脑电检测研究(见表3)。Khan and Gotman 提出了一种利用小波相对能量、方差函数和相对幅度作为特征的癫痫检测方法［1］。该方法对来自11 位患者含有66 次癫痫发作的长程脑电数据进行检测，获得了87%的灵敏度。Majumdar 等利用窗口微分方差方法检测15 人59 h 癫痫脑电，所取得的癫痫检测灵敏度为91.5%［7］。Chua 等提出的患者相关检测方法对15 人63 次癫痫发作的检测灵敏度为78%［11］。Raghunathan 等人的多级癫痫检测方法对5 个患者24 次癫痫发作检测，所取得的灵敏度为87.5%。本方法对18 个患者66 次癫痫发作的长程脑电数据检测的灵敏度达到了94.2%，与上述结果相比，获得了更高的检测灵敏度。

表3 颅内脑电癫痫检测方法的结果比较Tab．3 Result comparison of different seizure detection methods with intracranial EEG

5 讨论

本检测方法使用了3 种脑电特征:微分方差、相对能量和波动指数。其中，微分方差特征有效地利用微分运算处理脑电信号，更加突出了癫痫脑电的特征波，使得发作期的癫痫波与不发作的背景波之间的差异更加明显，然后通过计算方差得到两类脑电信号的统计特征。当癫痫发作时，脑电信号呈现出高幅的节律波，并且其能量主要集中在有限频带内。相对能量特征正是利用该现象，通过计算个别频带能量与总能量的比值来区别癫痫发作期与未发作的间歇期。此外，癫痫发作时脑电信号的波动会比未发作的间歇期剧烈，而波动指数直观地描述了信号的变化强度。本研究通过计算相对于背景波的波动指数，进一步突出了癫痫波的波动特性，有利于对癫痫发作的检测。联合微分方差、相对能量和波动指数这3 种特征，通过贝叶斯公式计算待检脑电信号为癫痫波的概率，实现癫痫检测，获得了94.2%的检测灵敏度。

检测方法所选用的3 种脑电特征均为线性特征，具有运算复杂度低的特点，有利于癫痫脑电的实时在线检测。

本研究所设计的分类器可直接用于新的脑电数据的检测。如果灵敏度偏低，则需对部分新数据进行训练，利用统计学原理对发作期和间歇期数据进行统计，求得癫痫脑电的先验概率和条件概率，然后对其余数据进行分类检测。

6 结论

本研究探讨了利用多特征对癫痫脑电信号进行自动检测的方法。通过对癫痫患者的长程颅内脑电进行实验评估，结果说明了本研究所选微分方差、相对能量和波动指数特征可以较好地描述癫痫发作，区分发作期和间歇期的脑电信号，实现癫痫自动检测。多特征联合提高了癫痫检测的性能。贝叶斯分类器结合可以调节的阈值，使得检测结果具有较高的灵敏度和较低的误检率。所提出的癫痫波自动检测的方法具有较好的临床应用潜力，值得进一步研究和探讨。

［1］ Khan YU，Gotman J. Wavelet-based automatic seizure detection in intracerebral electroencephalogram ［ J ］. Clinical Neurophysiology，2003，114(5):898 -908.

［2］ Gotman J，Gloor P. Automatic recognition and quantification of interictal epileptic activity in the human scalp EEG［J］.Electroencephalography and Clinical Neurophysiology，1976，41(5):513 -529.

［3］ Gotman J. Automatic recognition of epileptic seizures in the EEG［J］. Electroencephalography and Clinical Neurophysiology，1982，54(5):530 -540.

［4］ Pradhan N，Dutt D，Satyam S. A mimetic-based frequency domain technique for automatic generation of EEG reports［J］.Computers in Biology and Medicine，1993，23(1):15 -20.

［5］ Sankar R，Natour J. Automatic computer analysis of transients in EEG［J］. Computers in Biology and Medicine，1992，22(6):407 -422.

［6］ Grewal S，Gotman J. An automatic warning system for epileptic seizures recorded on intracerebral EEGs ［J］. Clinical Neurophysiology，2005，116(10):2460 -2472.

［7］ Majumdar KK，Vardhan P. Automatic seizure detection in ECoG by differential operator and windowed variance［J］. IEEE Transactions on Neural Systems and Rehabilitation Engineering，2011，19(4):356 -365.

［8］ Saab M，Gotman J. A system to detect the onset of epileptic seizures in scalp EEG［J］. Clinical Neurophysiology，2005，116(2):427 -442.

［9］ Yuan Q，Zhou W，Liu Y，et al. Epileptic seizure detection with linear and nonlinear features［J］. Epilepsy and Behavior，2012，24:415 -421.

［10］ 蔡冬梅，周卫东，李淑芳，等. 基于去趋势波动分析和支持向量机的癫痫脑电分类［J］.生物物理学报，2011，27(2):175 -182.

［11］ Chua E，Patel K，Fitzsimons M，et al. Improved patient specific seizure detection during pre-surgical evaluation［J］. Clinical Neurophysiology，2011，122(4):672 -679.

［12］ Raghunathan S， Jaitli A， Irazoqui PP. Multistage seizure detection techniques optimized for low-power hardware platforms［J］. Epilepsy and Behavior，2011，22:S61 -S68.