基于邻域粗糙集与量子遗传算法的人脸表情特征选择方法
2013-03-07冯林,李聪,沈莉
冯 林, 李 聪, 沈 莉
(四川师范大学 计 算机科学学院,四川 成 都 610068)
0 引 言
近年来,自然人机交互技术日益成为人工智能研究领域的热点,赋予计算机情感能力的研究得到广泛重视[1]。从心理学的观点看,表情是情感的主观体验的外部表现模式,人的表情主要有面部表情、语言声调表情和身体姿态表情3种方式。由于面部表情包含了丰富的情感信息,是人类情感交流的一个最重要载体,也是人们理解情感的重要途径,因此,面部情感的识别已成为情感计算中的一个重要研究课题,它是实现自然、和谐、拟人化的人机交互的必要环节之一[2-3]。
一般来说,面部表情识别系统通常包括人脸检测、表情特征提取、特征选择(即属性约简)和模式分类4部分。对人脸进行检测或跟踪确定人脸的位置是人脸检测研究的重要内容。目前,对于无大幅度晃动的正面人脸图像,基于Haar特征及Adaboost的人脸检测及脸部器官定位算法能够根据人脸及眼睛的准确定位,得到嘴巴、额头和眉毛的位置[4]。表情特征提取的关键是为了获取便于计算机处理且能较好刻画图像中人脸表情的特征。有关表情特征提取方面的众多方法中,基于几何特征的方法与基于外观特征方法是常用的2种方法[5]。特征选择可以删除冗余特征,保留对表情分类有用的重要特征;同时可以提高表情识别系统的实时性,而实时性对于表情识别系统是非常重要的,常用的特征选择方法有个人计算机助 理 (Persoral Computer Assistant,简 称PCA)、粗糙集理论等[6-7]。模式分类的关键是设计出能得到较高正确识别率的人脸表情识别方法。常用的模式分类方法有隐马尔可夫模型(HMM)、人工神经网络(ANN)、贝叶斯及支持向量机等[8]。
文献[7]建立了一个由33个面部表情几何特征构成的人脸表情特征数据,并提出了基于经典粗糙集理论的特征选择(属性约简)与表情分类方法。由于人脸表情特征数据是一个典型的连续值信息系统,用经典的粗糙集理论对连续值信息系统进行特征选择时,首先需要对连续值数据进行离散化处理,但离散化的过程可能导致信息的丢失,进而会影响到表情分类结果。目前,已有模糊粗糙集、邻域粗糙集模型等[9-10]有效方法解决这一问题。
研究证明,特征选择的复杂度随决策表条件属性个数的增长呈指数增长,是一个典型的NP问题。而遗传算法(Genetic Algorithm,简称GA)[11]具有全局搜索和隐含并行性,能够处理传统优化方法难以解决的问题等优点,因此将其用于特征选择可以避免因特征个数多而产生NP问题。但传统GA算法在实际应用中存在迭代次数多、收敛速度慢、易陷于局部极值和过早收敛等一些不足。因此,用量子遗传算法(Quantum Genetic Algorithm,简称QGA)弥补传统GA算法的缺陷,解决实际应用中的优化问题受到了广泛关注[12-13]。
本文首先对人脸表情几何特征的提取方法进行了扩展,根据邻域粗糙集理论,并结合量子遗传算法,提出了一种新的表情特征选择方法 (Feature Selection based on Neighborhood Rough Set Theory and Quantum Genetic Algorithm,简称FSNRSTQGA),并进行了仿真实验,得出了较好的实验结果。
1 人脸表情数据的特征提取
人脸表情特征提取在表情识别中处于核心地位,直接关系到表情识别率的高低。文献[7]基于人脸几何特征,提出了52个与面部表情特征相关的特征点,如图1所示。并对眼睛、鼻子、眉毛及嘴等的位置变化进行定位、测量,确定其大小、距离、形状及相互比例等特征,建立了一种新颖的人脸表情特征提取方法。基于文献[7]提出的人脸面部特征点,并考虑到面部表情的细微性与几何特征的可测量性,本文对该人脸表情几何特征进行了扩展,扩展后的表情特征包括35个距离特征,其定义见表1所列。
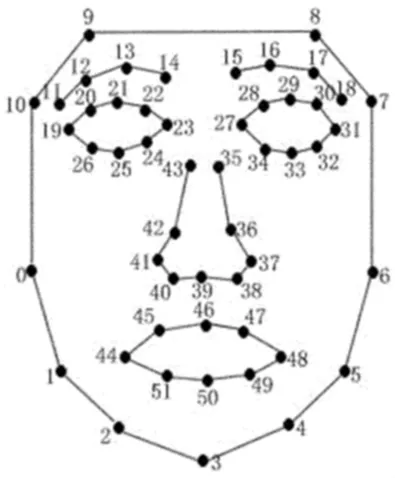
图1 52个面部特征点

表1 扩展的人脸表情几何特征的定义
表1中,A点为19和23的中点;B点为27和31的中点;dis(i,j)表示点i到点j的欧氏距离;hei(i,j)表示点i到点j的垂直距离;wid(i,j)表示点i到点j的水平距离。
2 表情特征选择方法
2.1 量子染色体
在QGA算法中,最小信息单元用量子位(量子比特,qubit)表示。一般地,一个量子位的状态可取0或1,又可以表示它们任意的线性叠加,可定义为:

其中,|0〉和|1〉分别表示自旋向下和自旋向上2种状态;α、β为相应状态出现概率的2个复数,分别表示|0〉和|1〉的概率幅,满足的条件为:

一个具有m个量子比特位的系统描述为:
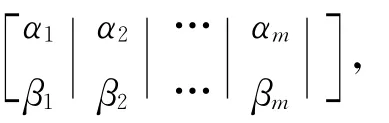
其中,|αi|2+|βi|2=1,i=1,2,…,m。
2.2 量子变异
在QGA算法中,用量子旋转门的旋转角度来表征量子染色体的变异,进而在变异中加入最优个体的信息,加快算法收敛。其定义为:
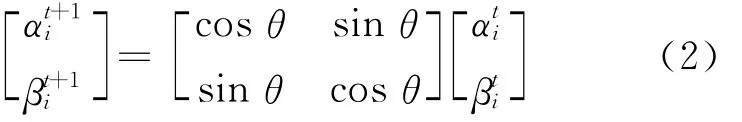
2.3 量子交叉操作
量子遗传算法中,搜索性主要通过交叉和变异实现。本文采用全干扰交叉来克服算法的早熟现象。在这种交叉操作中,种群中所有染色体均参与交叉,具体交叉操作见文献[12]。
2.4 适应度函数的选择
量子遗传算法在优化搜索中以适应度函数为寻优准则,适应度函数依据目标问题而定。量子遗传算法对适应度函数的要求为:该函数不能为负,且任何情况下适应度函数值越大越好。本文适应度函数基于邻域粗糙集理论[10],并扩展适应度函数[13]的定义如下。
定义1 给定决策表S= (U,C∪D,V,f),

其中,|pj|为pj中所含的条件属性个数;|C|为S中条件属性的个数;δ为邻域阈值;(D)为邻域粗糙集理论中C对D的δ分类精度[10]。
(4)式能保证当(D)与(D)接近时,f(pj)充分大,反之,f(pj)越小;当(D)=(D)且|pj|取最小值时,f(pj)取最大值。因此,在求解S中最小相对约简时保持条件属性子集pj对决策属性D的δ近似分类质量(或分类能力)不变的条件下,f(pj)具有所保留的条件属性最少的特点。
2.5 表情特征选择方法的运算步骤
算法1 FSNRSTQGA方法。
输入:S,种群规模n,最大迭代次数maxgen;输出:S的一个特征子集。
(1)种群P= {p1,p2,…,pn},进化代数初始值g=0,其中pj(j=1,2,…,n)为种群中的第j个个体,将pj中的所有基因(α,β)均初始化为其中C和D分别称为连续值条件属性集和决策属性集。对种群规模P= {p1,p2,…,pn}中的每个个体pj(j=1,2,…,n),其适应度函数f(pj)为:
(2)根据P中各个个体的概率幅构造出量子叠加 态 的 观 测态R,R= {a1,a2,…,an},其 中aj(j=1,2,…,n)为每个个体的观测态,且为一个长度为m的二进制串,即aj=b1b2…bm。随机产生0与1之间的一个数r,若r<|αi|2,则相应的观测值b为“0”;否则,相应的观测值b为“1”。
(3)用适应度函数f(pj)对种群中的每个个体进行评价,保留此代中的最优个体。
(4)使用量子门和量子全干扰交叉更新策略更新各染色体,g=g+1;若满足maxgen,则输出特征选择的结果,算法终止;否则,执行步骤(2)。
3 实验及结果分析
为了验证FSNRSTQGA方法的效果,本文从Cohn-Kanade人脸表情库中随机选取了405个图像样本,包括中性、高兴、惊奇、愤怒、悲伤、厌恶和恐惧共7种表情。由于Cohn-Kanade中并不是所有的人都有7种表情,每人的表情从2~7种不等。文中选取的405个样本中包括67个中性表情,65个高兴表情,68个惊奇表情,48个愤怒表情,58个悲伤表情,48个厌恶表情和51个恐惧表情。结合表1中的表情几何特征,使用文献[7]中的相关方法,可以得到405个样本,35个几何特征的连续值数据。为了减少因各属性量纲不一致对结果的影响,本文所有连续值属性用最大-最小值方法被标准化到[0,1]区间,其实验步骤如下。
(1)分别使用FSNRSTQGA方法和文献[7]方法对表情数据集进行属性约简(特征选择),并把约简后的表情数据作为SVM分类器的输入,采用10折交叉验证的方法进行测试,并输出识别结果。
(2)把未经过特征选择的表情数据(即原始数据集)作为SVM分类器的输入,采用10折交叉验证的方法进行测试,并输出识别结果。
FSRSTQGA方法具体的参数设置为:初始种群的数量为30,最大迭代次数700;支持向量机的参数设置为SVM Type:C-SVC,Kernel Function:RBF,Multiclass Method:one-against-one。在Cohn-Kanade人脸表情集上,由本文方法与文献[7]方法得到的特征选择(属性约简)的结果分别为14、10。SVM分类的实验结果见表2所列。从表2可知,本文方法、文献[7]方法和属性未约简时SVM 的总识别率分别为85.4%、82.9%、86.2%。本文方法仅用较少的特征子集取得了与特征全集差不多的分类结果,说明本文特征选择方法是有效的。同时可以看出,不同类别的表情识别率相差较大,如悲伤的识别率较低,主要原因是悲伤情感与中性情感相互混淆,不易区分。
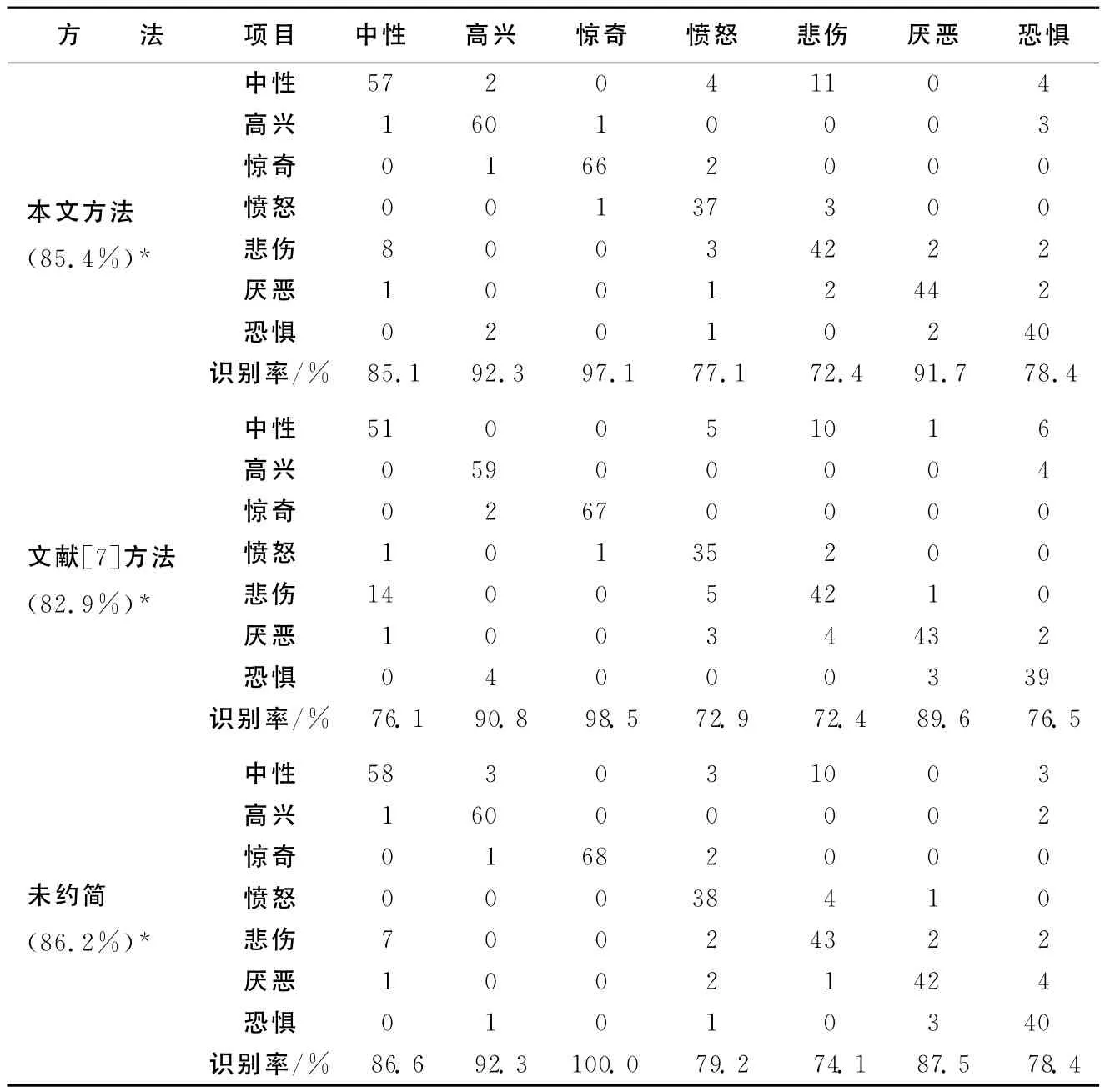
表2 不同方法SVM分类的实验结果
4 结束语
针对人脸表情的几何特点,在前人研究工作的基础上,本文对人脸表情几何特征的提取方法进行了扩展,并结合量子遗传算法与邻域粗糙集理论,提出了一种人脸表情特征选择方法FSNRSTQGA。在Cohn-Kanade人脸表情集上的实验表明,本文方法能有效地提取有利于表情分类的特征,获得了较为满意的结果。但由于人类情感过程的复杂性,如何设计更好的特征选择算法[14]以建立反应认知科学、心理学等方面的情感特征选择模型,仍有大量值得探索的课题。
[1] Picard R W.Affective computing:from laughter to IEEE[J].IEEE Transactions on Affective Computing,2010,1(1):11-17.
[2] 薛雨丽,毛 峡,郭 叶,等.人机交互中的人脸表情识别研究进展[J].中国图象图形学报,2009,14(5):764-772.
[3] 温万惠,邱玉辉,刘光远,等.情感生理反应样本库的建立与数据相关性分析[J].中国科学:信息科学,2011,41(1):77-89.
[4] 魏 冉,姜 莉,陶霖密.融合人脸多特征信息的表情识别系统[J].中国图象图形学报,2009,14(5):792-800.
[5] 山世光,高 文,陈熙霖.基于纹理分布和变形模板的面部特征提取[J].软件学报,2001,12(4):570-577.
[6] Calvo R A,D'Mello S.Affect detection:an interdisciplinary review of models,methods,and their applications[J].IEEE Transactions on Affective Computing,2010,1(1):18-37.
[7] Chen P J,Wang G Y,Yang Y,et al.Facial expression recognition based on rough set theory and SVM[J].Lecture Notes in Computer Science,2006,4062,772-777.
[8] 陈培俊.基于静态图像的人脸表情识别研究[D].成都:西南交通大学,2007.
[9] 冯 林,王国胤.用于数据分析的可变精度模糊粗糙数据模型[J].西南交通大学学报,2008,43(5):582-587.
[10] 胡清华,于达仁,谢宗霞.基于邻域粒化和粗糙逼近的数值属性约简[J].软件学报,2008,19(3):640-649.
[11] Holland J H.Adaptation in natural and artificial systems[M].Cambridge:MIT Press,1975:12-25.
[12] 焦李成,杜海峰,刘 芳,等.免疫优化计算、学习与识别[M].北京:科学出版社,2006:253-287.
[13] 冯 林.一种基于量子遗传算法与粗糙集理论的属性约简法[J].信息与控制,2011,40(2):198-201.
[14] 李 菊,刘晓平,谢从华.改进的特征选择算法在形状分析中的应用[J].合肥工业大学学报:自然科学版,2012,35(3):334-336.
