一种改进的标签传播快速社区发现方法
2013-03-07康旭彬贾彩燕
康旭彬, 贾彩燕
(北京交通大学 计 算机与信息技术学院,北京 100044)
0 引 言
现实世界中的很多数据都可以建模为网络形式,如社交网络、蛋白质作用网络、万维网、科学家合作网等等[1]。这些网络具有数据量大、结构复杂的特点,所以被称为“复杂网络”。随着科学研究的深入,人们发现这些网络通常蕴含一些统计特性,如小世界特性[2]、无尺度特性[3]、包含社区结构等。其中,“社区结构”作为复杂网络的一个重要拓扑属性,受到了人们的极大关注。所谓“社区”是指那些联系比较紧密的节点组成的点集。社区发现方法的研究对理解复杂网络的功能、预测复杂网络的行为以及分析复杂网络的拓扑结构具有重要的理论意义和广泛的应用前景,已被应用于社会网络分析、蛋白质交互网络分析、Web文档聚类等各个方面。目前,人们已经给出了多种社区发现方法。这些方法分为基于优化的社区发现方法、基于启发式策略的社区发现方法及其他方法3类。
基于优化的方法有谱方法和模块性最大化方法。其中,谱方法是对网络邻接矩阵A的拉普拉斯矩阵M(M=D-A)求特征值,D是由节点的度构成的对角矩阵,然后根据其最大特征值对应的特征向量对网络进行二分,如果需要划分成多个社区,一般采用不断二分的方法;模块性最大化方法,是对网络模块性函数(也称为Q函数)求最大值。Q函数是指社区内的实际连接数目与随机情况下社区内连接数目之差,可以在一定程度上衡量社区结构的好坏,Q函数的表达式为:
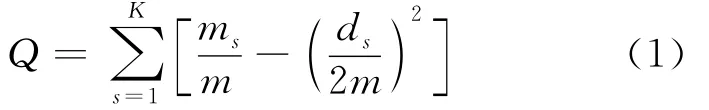
其中,K为网络社区数目;m为网络的连边数;ms为社区s中的连边数;ds为社区s中结点的度之和。
基于启发式策略方法有:GN算法[4]、WH算法[5]、MFC 算 法[6]、HITS 算 法[7]、CPM 算 法[8]等。其中,GN算法是一种基于局部搜索的社区发现方法,它通过反复识别和删除那些边介数最大的边来发现社区。边介数是指网络中经过该连边的任意2点间最短路径的数目。WH算法将网络建模为电路系统,网络中的连接看作是具有电阻的线路,不同节点具有不同的电势差。它的启发式规则是:当在不同的社区中选取2个节点作为正负极后,由于社区间的电阻要大于社区内的电阻,所以处于同一社区内节点的电势应该大致相同,而不同社区内节点的电势相差较大。
除此之外,还有其他一些有效的社区发现方法,如基于层次聚类的社区发现方法(凝聚式和分裂式)和基于非负矩阵分解的社区发现方法等。
现有的社区发现算法存在算法复杂度高、需要事先制定社区的数目和预先制定评价指标等缺陷,有的甚至需要给出大致的社区大小,因而限制了算法的实际应用效率。文献[9]提出了一种基于启发式策略的快速社区发现算法LPA(Label Propagation Algorithm,简称LPA),这种算法不需要指定社区数目且时间复杂度低,不需要设计目标函数,具有便于实现和大规模网络应用等特点,但相比于前述算法,该算法准确率比较低。文献[10-11]分别对该算法进行了改进,但是这2个改进的算法都引入了额外的参数,在实际的应用中这些参数往往难以确定。本文提出了一种改进的、基于相似性的、无参数的标签传播算法LPALS(Label Propagation Algorithm based on Local Similarity,简称LPALS),实验结果显示该算法大大提高了原有算法的准确率且具有较低的时间复杂度。
1 LPA算法
LPA算法的基本思想是一个节点的label决定于它的邻居节点。假设节点x的邻居节点有x1,x2,x3,…,xk,并且每个邻居都带有一个label表示它所属的社区,那么当某个社区包含x的邻居节点数最多时,x就属于这个社区。图1所示为节点1的更新过程,其中图1a中label为1的节点变为图1b中的3,因为它的邻居节点中label为3的节点数最多。
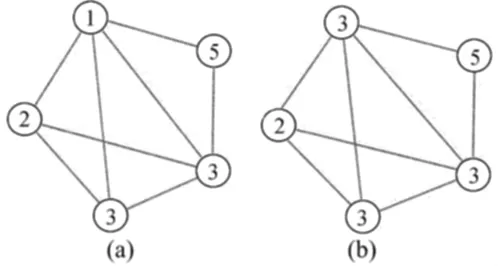
图1 LPA算法中节点1的更新过程
随着label的传播,那些连接稠密的节点会迅速得到一个一致的label。通过多次迭代,网络中各节点的label会趋于稳定,社团结构随即也会显现出来。
在LPA算法中节点的label有同步更新与异步更新2种更新方法。所谓同步更新,即节点x在第t次迭代的label依据于它的邻居节点在第t-1次迭代时所得的label,更新公式如下:
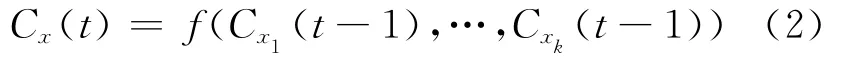
其中,Cx(t)表示节点x在t时刻的label,f函数返回的是在x的邻居节点里出现频率最高的那个label。如果有多个label出现的频率最高则从这些label中随机返回一个label。由于这种方法在二分图中可能产生震荡现象,于是给出了异步更新方法,其更新公式如下:
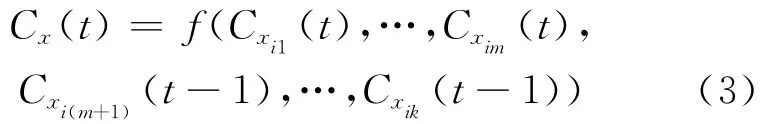
其中,xi1,…,xim表示在本次迭代中已经更新过label的节点;xi(m+1),…,xik表示 在此次迭代中label还没有更新的节点,f函数仍如上所述。因此,节点x在第t次迭代的label依据于第t次迭代已经更新过label的节点和第t次迭代未更新过label的节点在第t-1次迭代时的label。标签传播算法LPA的步骤如下:
(1)初始化网络中所有节点的label。
(2)迭代次数t=1。
(3)随机排列网络中的节点,生成序列X。
(4)for(x∈X),
Cx(t)=f(Cxi1(t),…,Cxim(t),Cxi(m+1)(t-1),…,Cxik(t-1))。
(5)若所有节点的label都不再变化则结束,否则t=t+1并且返回步骤(3)。
如前所述,这个算法简单、高效,但准确率还有待提高。原因之一是不同社团之间节点的label很容易传播,如图2所示,图2a中label为5的节点如在图2b中变为label为4的节点,则整个网络的所有节点的label在图2c中都为4。
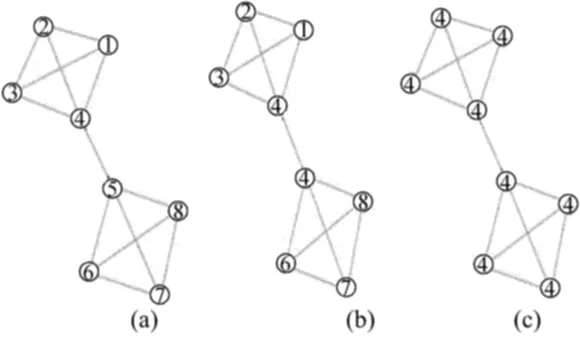
图2 不同社团间节点label的传播
2 改进的LPA算法
分析发现LPA算法的准确率低是因为在label的更新过程中平等地对待了每一个邻居节点的label从而导致不同社区间的label很容易传播。为了阻止这种情况发生,可以给每个label分配一个权值,当节点x的某个邻居节点与x属于同一社区的可能性大时这个权值就大,反之则小。可以用节点间的某种拓扑相似度表示权值。其中,常用的基于局部拓扑信息的相似度主要有如下3种:
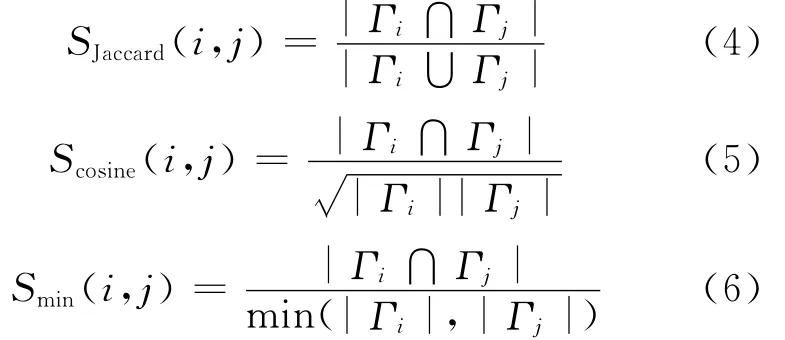
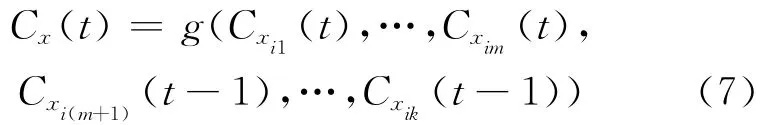
其中,Γi表示节点i的邻居集合;|Γi|表示该集合的势;Γi∩Γj表示节点i和节点j的共同邻居数。在本文的算法中,使用第3种相似度,则节点x的label更新公式变为:其中,g返回的是在x的邻居节点里出现的权值之和最大的label,若存在多个这样的label,则随机选择一个作为x的label。这就在很大程度上限制了不同社区间label传播的随意性。也就是说label的传播被限定在与该节点距离最小的社区中,称这种方法为基于相似性的标签传播LPALS(Label Propagation Algorithm based on Local Similarity)。在这种情况下,图2a中label加了权,节点5的label不会变成4,如图3所示。
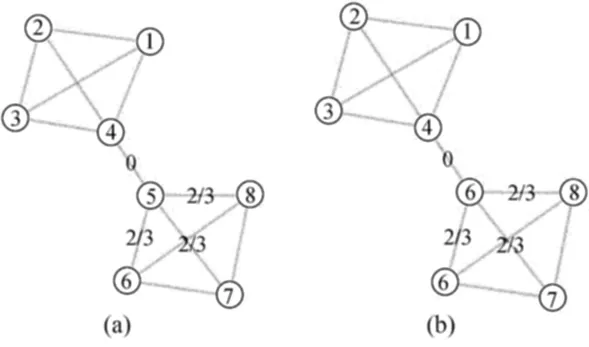
图3 加权后节点5的label的传播
算法LPALS的具体步骤如下:
(1)初始化网络中所有节点的label。
(2)计算所有连接的权值,即2个节点的局部相似度。
(3)迭代次数t=1。
(4)随机排列网络中的节点,生成序列X。
(5)for(x∈X),
Cx(t)=g(Cxi1(t),…,Cxim(t),Cxi(m+1)(t-1),…,Cxik(t-1))。
(6)若所有节点的label都不再变化则结束;否则t=t+1并且返回步骤(4)。
易知该算法的时间复杂度为O(m+n),其中,m为网络中的边数,n为网络中的节点数。
3 实验结果及分析
本节主要是LPA算法与LPALS算法在人工基准网络与真实网络上的实验结果对比,由于这2种算法都具有一定的随机性,所有实验结果都取10次实验的平均值。
3.1 LFR基准网络实验结果
LFR基准网络[12]被广泛应用于测试社区发现算法的性能。这种网络能生成符合用户指定分布的网络,更接近真实的情况,这里的分布不仅包括网络节点度的分布,而且包括各个社区中节点数的分布。本文中所使用的网络节点度最大为50,最小为20,并且服从指数为2的幂律分布。在含有1 000和5 000个节点的网络中,社区中的节点数最大为50,最小为10,并且服从指数为1的幂律分布。在含有10 000个节点的网络中,社区中的节点数最大为100,最小为20,并且服从指数为1的幂律分布。参数μ表示社区的明显程度,范围从0到1,它表示网络中处于社区之间的边数与网络总边数的比值,所以μ值越大社区结构越不明显。
在节点数为1 000(小规模)、5 000(中等规模)、10 000(较大规模)的网络上,测试了LPA算法与改进的LPALS算法的性能。其中,μ值从0.1向0.9变化,步长为0.1,对比结果如图4~图6所示。
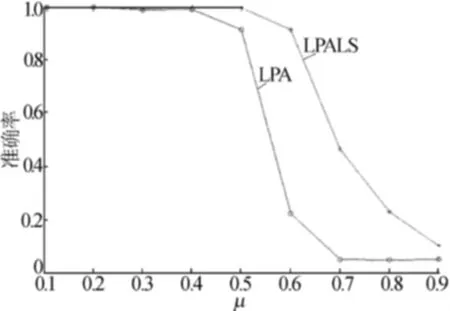
图4 1 000节点实验结果对比
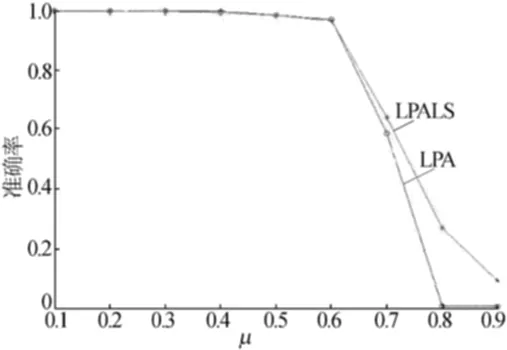
图5 5 000节点实验结果对比
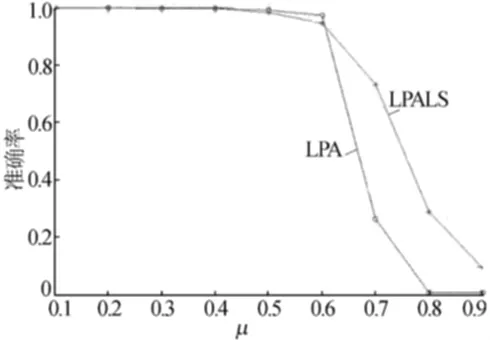
图6 10 000节点实验结果对比
从图4~图6可以看出,当社区结构比较明显时2种方法的准确率都较高,但是当社区结构变得复杂时,LPALS算法的准确率要明显高于原始的LPA方法。
另外,在节点数为1 000、5 000、10 000的网络上,在不同的μ值下测试了LPA算法与LPALS算法的执行效率,结果见表1~表3所列。
从表1~表3中可以看出,LPALS算法的运行时间和LPA算法相比并没有太多增加,在提高了准确率的前提下,运算时间的增加是可以接受的。

表1 1 000节点运行时间对比 s

表2 表2 5 000节点运行时间对比 s

表3 表2 10 000节点运行时间对比 s
3.2 真实网络实验结果
选用常用的 Zachary Karate网络[13]、College Football网络对算法LPA及LPALS进行测试分析。表4、表5分别为Zachary空手道俱乐部网络、美国大学橄榄球联盟网络运行2种算法的结果对比,结果用准确率表示。

表4 Karate网络实验结果

表5 Football网络实验结果
为了进一步验证算法的有效性,选择较大的蛋白质交互网络[14]和 Email网络[15]对算法 LPA及LPALS进行测试分析。蛋白质交互网络的实验结果见表6所列。由于Email网络没有标准的社区结构,所以采用计算Q函数的方法来比较这2种算法,结果见表7所列。
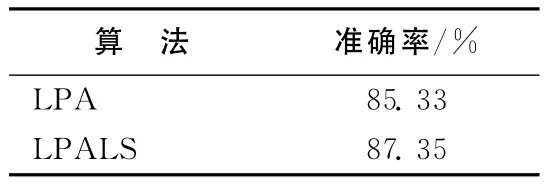
表6 蛋白质作用网络实验结果

表7 Email网络实验结果
从表4~表7的对比结果可以看出,LPALS在真实网络上的准确率或Q函数高于LPA。
4 结束语
本文基于网络中节点的拓扑相似性,给出了一种改进的标签传播算法LPALS,在有效继承了LPA算法优点的同时,提高了LPA算法的精度。该算法的精确度相比于适用于小规模网络的、高复杂度的算法来说,精确度还有待进一步提高。
[1] 杨 博,刘大有,Liu Jiming,等.复杂网络聚类方法[J].软件学报,2009,20(1):54-66.
[2] Watts D J,Strogatz S H.Collective dynamics of Small-World networks[J].Nature,1998,393(6638):440-442.
[3] Barabási A L,Albert R.Emergence of scaling in random networks[J].Science,1999,286(5439):509-512.
[4] Newman M E J.Modularity and communities structure in networks[J].Proceedings of the National Academy of Science,2006,103(23):8577-8582.
[5] Guimera R,Amaral L.Functional cartography of complex metabolic networks [J].Nature,2005,433 (7028):895-900.
[6] Flake G W,Lawrence S,Giles C L,et al.Self-organization and identification of Web communities[J].IEEE Computer,2002,35(3):66-71.
[7] Kleinberg J M.Authoritative sources in a hyperlinked environment[J].Journal of the ACM,1999,46(5):604-632.
[8] Palla G,Derenyi I,Farkas I,et al.Uncovering the overlapping community structures of complex networks in nature and society[J].Nature,2005,435(7043):814-818.
[9] Raghavan U N,Albert P,Kumara S.Near linear time algorithm to detect community structure in large-scale networks[J].Physical review E,2007,76(3):036106.
[10] Pan Ying,Li Dehua,Liu Jianguo,et al.Detecting community structure in complex networks via node similarity[J].Physical A:Statistical Mechanics and its Applications,2010,389(14):2849-2857.
[11] Xie J,Szymanski B K.Community detection using a neighborhood strength driven label propagation algorithm[C]//Network Science Workshop,2011:188-195.
[12] Lancichinetti A,Fourtunato S,Radicchi F.Benchmark graphs for testing community detection algorithm [J].Physical review E,2008,78(4):046110.
[13] Zachary W W.An information flow model for conflict and fission in small groups[J].Journal of Anthropological Research,1977,33(4):452-473.
[14] Jeong H,Mason S P,Barabasi A L,et al.Lethality and centrality in protein networks[J].Nature,2001,411(6833):41-42.
[15] Guimera R,Danon L,Diaz-Guilera A,et al.The real communication networks behind the formal chart:Community structure in organizations[J].Journal of Economic Behavior,2006,61(4):663-667.
