一种电大目标散射特性的核外并行快速算法

吴君辉 曹祥玉 袁浩波 高 军 封同安

（1.空军工程大学信息与导航学院，陕西 西安710077；2.西安电子科技大学 天线与微波技术国防重点实验室，陕西 西安710071）

引 言

矩量法（method of moments，MoM）作为一种严格的数值方法，可以精确分析目标的雷达散射截面（Radar Cross Section，RCS），随着计算机技术的发展，得到了越来越广泛的应用.但它在处理电大尺寸目标问题时，随着未知量数目的增多，所需时间和计算资源急剧上升.为降低MoM所需内存和计算量，出现了多种快速算法.其中自适应交叉近似算法［1］（Adaptive Cross Approximation Algorithm，ACA）是利用线性相关性来对低秩矩阵进行压缩，可将存储量和计算量降为O（N4／3logN）.由于ACA算法是从分组入手，将阻抗矩阵分解成一系列子矩阵块并对其进行压缩，所以，算法本身需要对阻抗矩阵进行分组［2］，这与核外求解［3］不谋而合，将阻抗矩阵按ACA分组压缩后存储在硬盘中，计算时每次只将计算所需的分组子矩阵读入内存.同时，为加快求解速度，可以采用并行计算［4-6］的方法，由不同的进程分别完成不同分组的填充、压缩和求解.总而言之，ACA算法的分组特性使得核外并行计算无需额外的工作量进行分块和分配进程，非常适合于进行核外并行化设计.

1 ACA算法基本原理

ACA算法是利用远场组所形成的阻抗矩阵具有的低秩特性，对其进行分解，用一对具有低秩特性的矩阵块来代表MoM中的远场相互作用，从而有效地对矩阵块进行压缩［7］.如图1所示，白色区域为自作用组，浅色区为近场组，不具有低秩特性，完全存储MoM阻抗矩阵填充的计算结果；而深色区域为远场组，可以采用ACA算法进行分解压缩.Zm×n代表MoM中两个远场组的互阻抗［8］，ACA算法采用两个满秩矩阵乘积的形式构造来近似表达Zm×n，即：

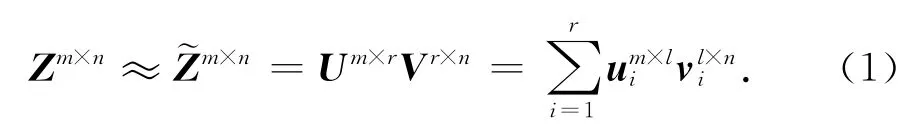
式中：r为矩阵Zm×n的有效秩；Um×r和Vr×n为两个满秩矩阵.秩r的选取根据下式得到［9］：

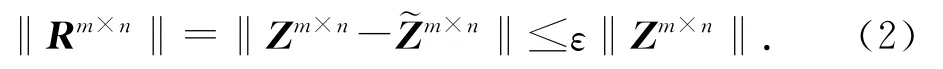
式中：ε为误差迭代门限；R为误差矩阵；‖·‖是矩阵的Frobenus范数.

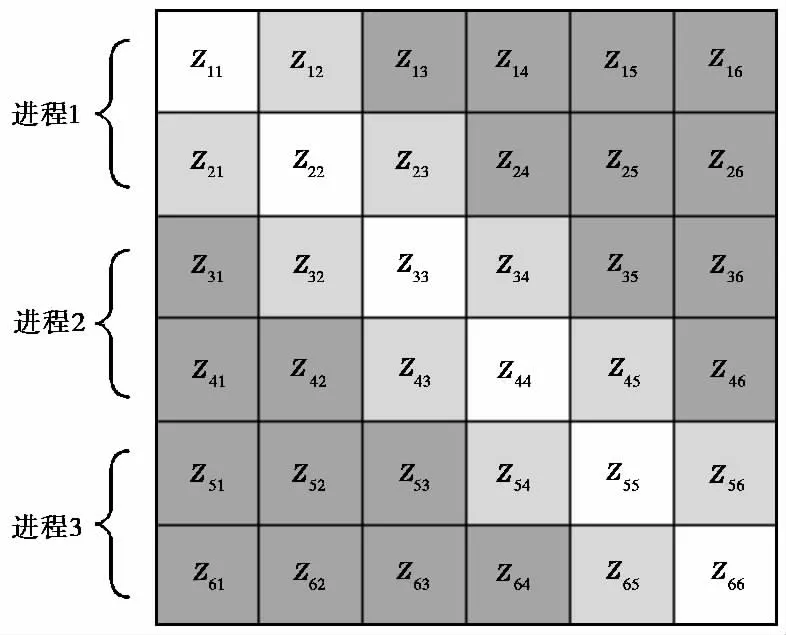
图1 阻抗矩阵分组示意图

当Zm×n用Um×r和Vr×n两个矩阵表示时，存储量由m×n变为r×（m＋n）.若r×（m＋n）＜m×n（通常r≪min（m，n）），则ACA算法只需保存Um×r和Vr×n这两个规模较小的矩阵，从而实现了矩阵的压缩.

2 核外并行计算

2.1 阻抗矩阵填充的核外并行化设计

ACA算法的阻抗矩阵填充是按分组逐块进行的，可以由不同进程填充并压缩不同子矩阵块.由于每个子矩阵块可以独立计算无需通信，并且每个分组计算量相似，只需简单的按分组行进行进程分配，将分组行平均的分为N片，分别分配给N个进程.如图1中，ACA算法将基函数分为6组，则阻抗矩阵由6×6的子矩阵组成，由三个进程并行运算，则整个矩阵分为三个行条带，每个进程包含两行子矩阵分组.

RWG（Rao-Wilton-Glisson）基函数是用共边的三角形作为基本面元形式，由于三角形具有良好的描述复杂模型的能力，并且RWG基函数易于实现ACA算法的分组，采用RWG函数作为基函数和权函数.由于基函数和权函数定义在三角形的公共边上，一个阻抗矩阵元素Zmn的计算要涉及到源三角形对中的与场三角形对中的之间的四次相互作用，分别记为，将这两个三角形对的四项位函数积分结果乘以合适的系数累加后，方可获得阻抗矩阵元素的完整值［10］.也就是说如果每个阻抗矩阵元素都独立计算势必会重复计算源面片与场面片的作用.ACA算法的分组不是简单的将阻抗矩阵划分为若干个子矩阵，而是将模型进行分片，使同一分组的基函数在模型中对应的位置在同一片连续的区域中.所以，位于同一个三角形的三条公共边通常位于同一个分组中，即相同的源三角形和场三角形将与同一子矩阵中的9个元素有关，最多将重复计算8次.为避免重复计算，在每个子矩阵的计算过程中，动态的建立一个二维数组Tmn（m，n），m为子矩阵中涉及的场三角形个数，n为子矩阵中涉及的源三角形个数，若某两个源三角形和场三角形的相关位函数已被计算过，将其记录在Tmn数组的相应位置中.当另一个阻抗矩阵元素的计算中包含此位函数，则可以直接带入，无需重新计算.阻抗矩阵并行填充的具体流程如图2所示.

当一个子矩阵完成填充和压缩后，将这个子矩阵的数据写入文件存储到硬盘上［3］，可以释放占用的内存，用于进行下一个子矩阵块的计算，从而在一定程度上解决内存不足的问题.

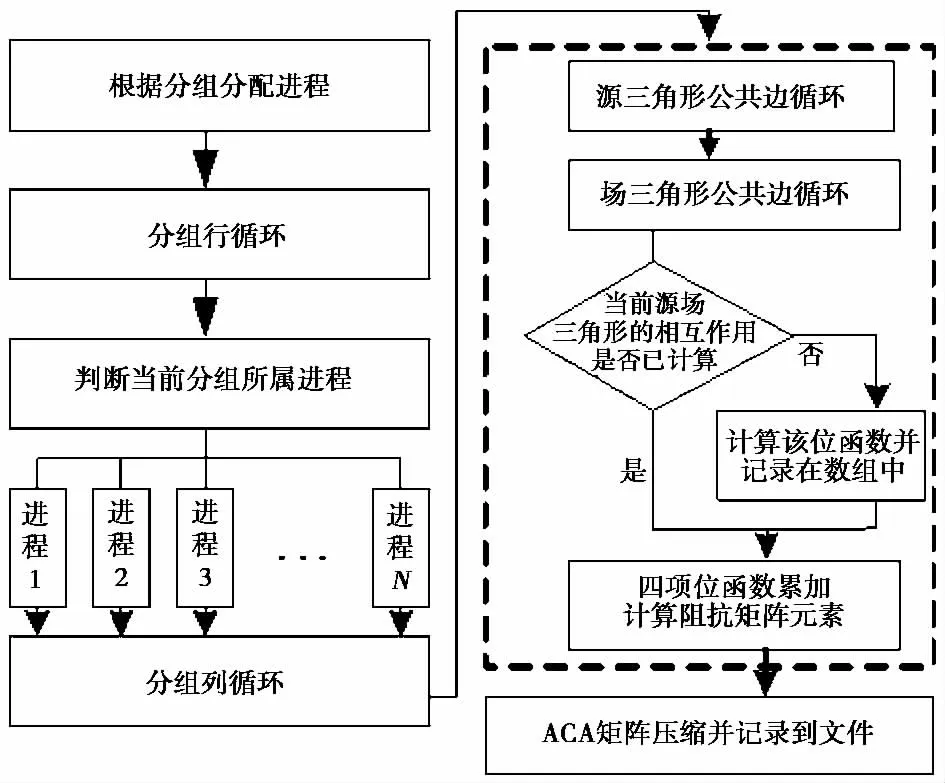
图2 核外并行填充流程示意图

2.2 核外并行CGNR求解矩阵方程

当整个阻抗矩阵压缩并记录完毕后，即开始对矩阵方程进行求解.针对上述核外存储方式，采用与矩阵填充相同的并行分配方式进行共轭梯度残差法（conjugate gradient residual method，CGNR）迭代求解.

CGNR提速的关键步骤就是计算阻抗矩阵A与向量x以及厄米矩阵A＋与x的矩量向量乘积运算.因此，首先讨论如何并行求解Ax、A＋x.对于Ax，仍将矩阵分为三个行条带，分别由三个进程求解，如图3所示.

由于每个进程的计算都需要用到矢量x的全部值，在计算前需要由主进程向其它两个进程发送矢量x的值.阻抗矩阵每行由六个子矩阵组成，根据矩阵填充和压缩的顺序，是按照从左到右的顺序依次存储在每个进程所属的核外文件中.出于内存容量有限的考虑，每次只从核外读取一块子矩阵的数据，并与x的相应区域作矩阵矢量乘，记录下结果后再读取下一组数据，分块如图4所示.当一行分组读取完毕后，将结果全部累加，即可得到该行所对应的结果矢量w部分区域的值，例如第一行的计算可表达为：

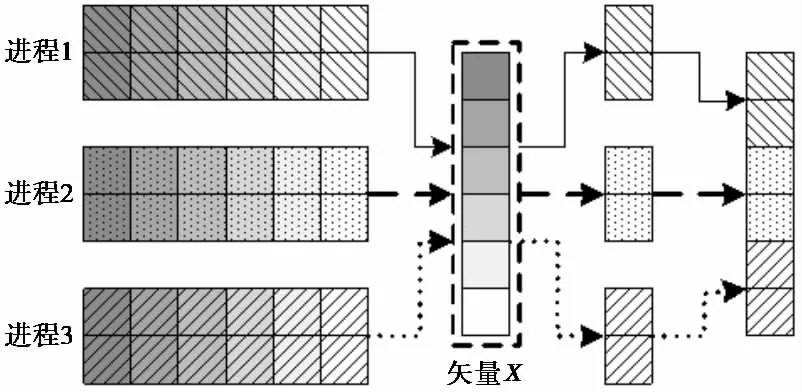
图3 各进程的子矩阵与向量相乘

当三个进程分别计算完毕后，将结果汇总至主进程组合起来，即可得到最终的结果矢量w.A＋x的计算可采用相同方法并行计算，这里不再赘述.

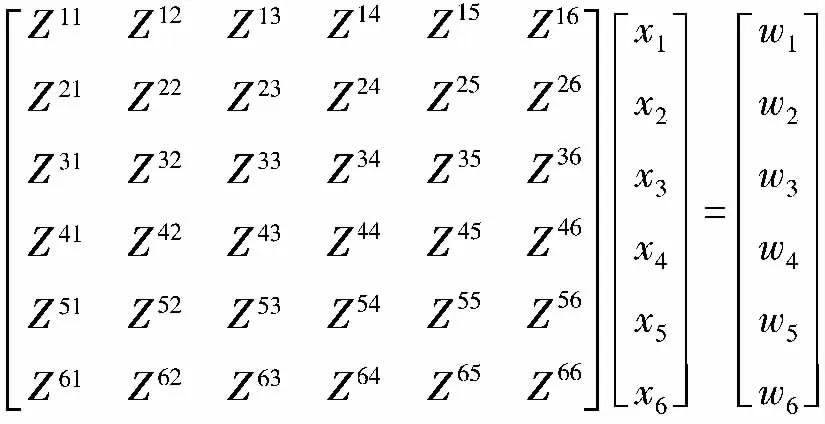
图4 阻抗矩阵与向量的分组

3 计算实例

算例所采用的计算机配置为Intel 3.6GHz CPU，2GB内存，160G硬盘.

计算如图5所示金属圆球的RCS并与Mie级数对比以验证算法的准确性.球半径为1m，剖分尺寸0.06m，剖分为2 724个三角形面片，未知数4 086个.激励平面波的频率为300MHz，由-z方向入射，沿x方向极化.如图5所示，核外并行ACA、ACA算法与MoM计算结果一致，与Mie级数结果吻合良好，说明ACA算法不损失MoM计算精度，且核外并行计算不影响ACA的计算结果.

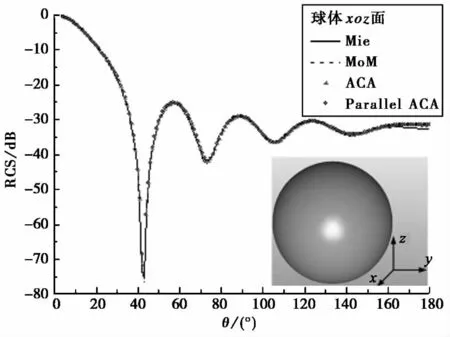
图5 球体xoz面上归一化RCS

接着为进一步验证算法求解电大问题的有效性和稳定性，计算一金属导弹模型，电尺寸约14λ×12λ×3λ，剖分为30 780个三角形面片，未知数为46 170.MoM理论需内存16.26GB，超过普通计算机物理内存，采用ACA算法需占用内存1.91GB，也超过了单机计算机的可用内存.采用核外并行ACA算法可以计算得到导弹的RCS，结果如图6所示.

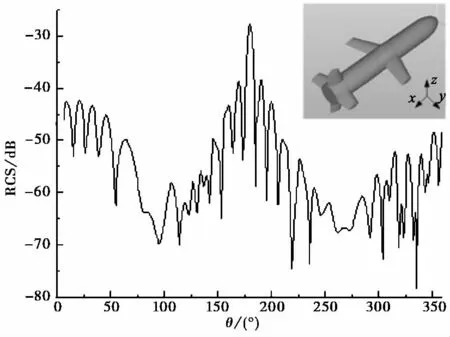
图6 金属导弹xoz面RCS

表1记录了采用不同进程数，核外并行ACA算法的矩阵填充和迭代求解时间情况，可见，并行的进程越多，计算时间越短，可以有效提高计算效率.在采用双进程计算时加速比可达到1.9，比较接近理想值2，当进程增多时，加速比的提高比例变小，这是由于进程越多，进程间通信时间占的比例越大造成的.因此如何降低通信时间，也是将来研究的一个重要方面.

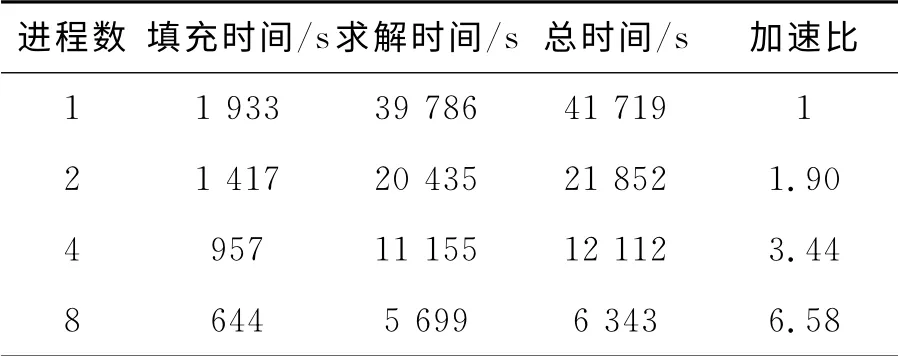
表1 不同进程数性能比较

4 结 论

计算机物理内存的限制是求解电大物体RCS的瓶颈.核外求解技术通过硬盘读写释放了内存空间，并行计算可以分解计算压力，提高计算速度.结合ACA算法本身对矩量法存储量和计算量的降低，核外并行ACA算法可以大大提高计算机的计算能力，降低大型计算的硬件需求和计算时间.计算结果表明：此算法有效地降低了计算所需内存空间和计算时间，并且不影响计算精度.

［1］BEBENDORF M.Approximation of boundary element matrices［J］.Numer Math，2000，86（4）：565-589.

［2］ZHAO K，VOUVAKIS M N，LEE J F.The adaptive cross approximation algorithm for accelerated method of moments computations of EMC problems［J］.IEEE Trans EMC，2005，47（4）：763-773.

［3］徐晓飞，曹祥玉，高 军，等.基于核外求解方法的电大目标散射特性计算［J］.电波科学学报，2010，25（4）：679-683.XU Xiaofei，CAO Xiangyu，GAO Jun，et al.Scattering calculation of electrically large targets based on out-ofcore solving method［J］.Chinese Journal of Radio Science，2010，25（4）：679-683.（in Chinese）

［4］袁 军，邱 扬，刘其中，等.自适应多层快速多极子算法及其并行算法［J］.电波科学学报，2008，23（3）：454-459.YUAN Jun，QIU Yang，LIU Qizhong，et al.Adaptive multilevel fast multipole algorithm and its parallel algorithm［J］.Chinese Journal of Radio Science，2008，23（3）：454-459.（in Chinese）

［5］JAIME L，MARCOS R P，RAJ M，et al.Parallelized multilevel characteristic basis function method for solving electromagnetic scattering problems［J］.Microwave and Optical Technology Letters，2009，51（12）：2963-2969.

［6］潘小敏，盛新庆.电特大复杂目标电磁特性的高效精确并行计算［J］.电波科学学报，2008，23（5）：888-893.PAN Xiaomin，SHENG Xinqing.Efficient and accurate parallel computation of electromagnetic scattering by extremely large targets［J］.Chinese Journal of Radio Science，2008，23（5）：888-893.（in Chinese）

［7］SHAEFFER J.Direct solve of electrically large integral equations for problem size to 1Munknowns［J］.Antennas and Propagation，2008，56（8）：2306-2313.

［8］YAN Ying，ZHANG Yu，ZHAO Xunwang.Timedomain method of moments accelerated by adaptive cross approximation algorithm［J］.APSURSI，2012，8（14）：1-2

［9］GUO Han，HU Jun，NIE Zaiping.Accelerating calderón multiplicative preconditioner with multi-grade adaptive cross approximation algorithm［J］.APSURSI，2011，3（8）：201-204.

［10］张 玉，王 萌，梁昌洪，等.PC集群系统中MPI并行矩量法研究［J］.电子与信息学报，2005，27（4）：647-650.ZHANG Yu，WANG Meng，LIANG Changhong，et al.Study of parallel MoM on PC clusters［J］.Journal of Electronice ＆Information Teohnology，2005，27（4）：647-650.（in Chinese）