多精度仿真方法及其在天线优化设计中的应用

裴进明 陈晓辉

（安徽工程大学电气工程学院，安徽 芜湖241000）

引 言

天线种类繁多，结构上的小型化，性能上的多频段、宽带化成为普遍趋势，而作为主要设计工具的电磁仿真软件却存在资源占用高、计算量庞大的缺点，难以实现模型的快速优化设计.近年来对经典电磁算法的替代与改进成为研究的热点，提出的算法包括代理模型法［1］、遗传算法［2］、支持向量回归法［3-4］，空间映射法［5-6］、模糊 递归法［7］、神经网络法［8-9］、分层算法［10］.这些算法大多使用智能算法而非数值计算来模拟结构和性能之间的关系，提高了计算效率，但是智能算法需要仿真数据作为先验知识，适用于尺寸变化但结构相近的系列天线设计，如八木天线、分形天线［8］等.

在不具备先验知识条件下，文献［11］提出使用粗糙模型并在设计流程中不断细化的方法，优点是在设计初始阶段减少计算量，探索粗糙模型的性能空间并在精细模型中实现.具体方法上文献［12-13］采用调整网格大小控制模型精度，定义适应度函数，由粗糙模型到精细模型用网格搜索寻找最优解.

基于由粗糙模型到精细模型的设计思想，以递增的网格数量构建粗糙模型集，在不同精度的粗糙模型上用可变的搜索步长进行区域搜索和方向搜索，寻找适应度函数最优解并将其作为下一级模型的初始值，在最后一级粗糙模型上利用二次回归小范围拟合结构参数与响应的关系，遍历解空间获得最优参数向量.该方法的有效性通过一个双频无线局域网络WLAN天线的仿真设计得到了验证.

1 理论分析

1.1 优化问题描述

天线优化问题可以描述为

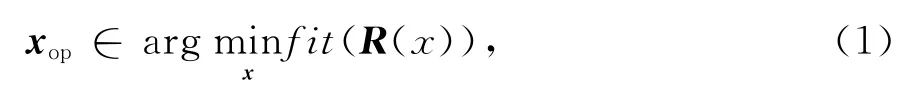
式中：x＝（x1，x2，…，xn）为参数向量空间，一般为天线结构中待优化变量；R＝（R1，R2，…，Rm）为响应向量空间，对于阻抗带宽优化而言，Rn可以是带宽内频点fn的回波损耗；fit为适应度函数，函数值越小，天线性能越好；xop为使fit函数达到最小的参数向量.优化过程即为寻找xop的过程.

1.2 粗糙模型

参数向量到响应向量的计算由电磁仿真软件完成时，需要对结构进行网格剖分并求解矩阵方程，计算效率低，优化时间长.为减小计算量构建粗糙模型集｛Rc.1，Rc.2，…，Rc.j，…，Rc.K｝，从Rc.1到Rc.K网格数量递增，对响应向量的计算精度逐渐逼近精细模型R.实际中粗糙模型的个数通常为2～3个［13］.

1.3 基于粗糙模型的优化

由于粗糙模型的计算量小，可以进行大范围搜索寻找最优向量.为了提高搜索效率，算法采用区域搜索和方向搜索相结合的方式，即首先根据第j个粗糙模型Rc.j的初始参数向量x（j）和参数向量的扰动向量d（j），计算初始参数向量及其附近区域2n个参数向量的适应度函数（fn，…，f1，f0，f-1，…，f-n）：

根据扰动向量引起的适应度变化，计算方向搜索的方向向量并归一化

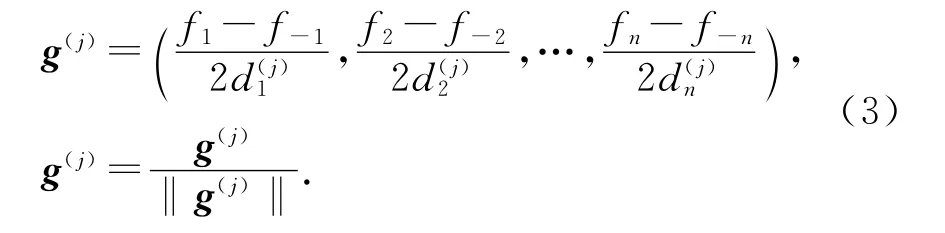
执行方向搜索

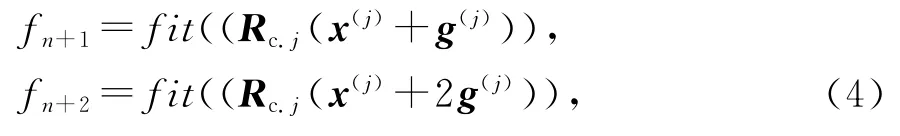
收敛准则为

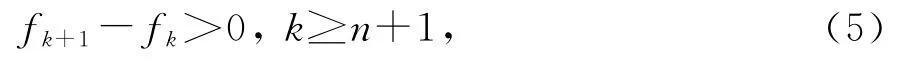
找出f-n，…，fn，fn＋1，fn＋2，…中最小值及其对应参数向量xop（j），作为下一级粗糙模型初始值重复优化过程.

1.4 参数向量到响应向量的拟合

各级粗糙模型中最后一级Rc.K网格数最多、精度最高，但计算量也最大，同时考虑到参数向量空间在本级最小，响应向量的线性度提高，因而采用回归方法拟合参数向量与响应向量的关系，为提高拟合精度，采用二次模型，即

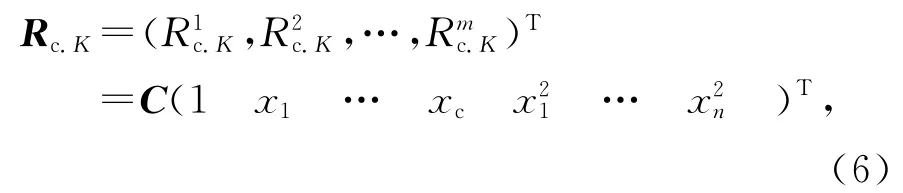
式中

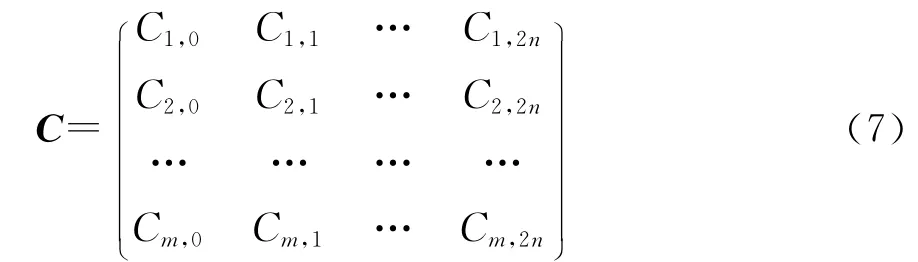
为系数矩阵.将区域搜索中初始参数向量x（K）及其附近2n个参数向量的响应向量作为样本数据，可以确定系数矩阵C.然后遍历参数向量空间［x（K）-d（K），x（K）＋d（K）］，每个参数向量只需一次矩阵乘法即可得到响应向量.考虑到粗糙模型Rc.K与精细模型R的误差，仿真精细模型x（K）的响应向量R（x（K）），计算R（x（K））-Rc.K（x（K）），对其它拟合出的数据做修正.计算R（x（K））是优化过程中唯一一次精细模型上求解.这个优化过程可以描述为

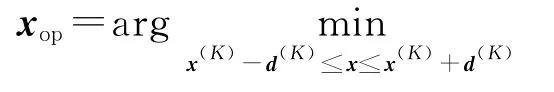
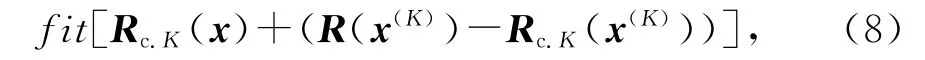
xop即为最优参数向量.

图1为K＝3时的优化过程，x（1）为初始参数向量，使用粗糙模型Rc.1求解其临近区域1、2、3、4的响应向量，并计算各点适应度，按式（3）计算方向向量进行方向搜索，求解5、6、7的响应向量，将1～7中最优参数向量作为Rc.2的初始参数向量并重复优化过程.在最后一级粗糙模型Rc.3上，求解初始参数向量x（3）及其临近区域的响应向量，拟合Rc.K（x）～x，求解式（8）得到最优参数向量xop.

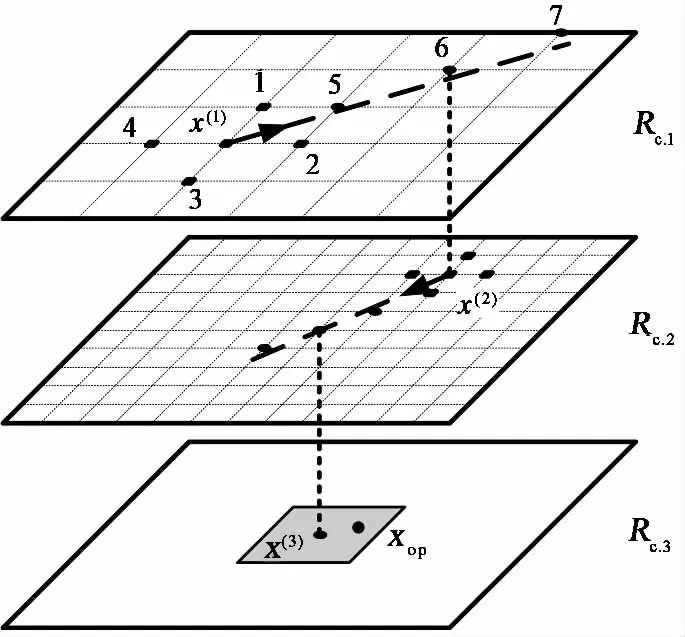
图1 优化过程示意图

2 实验结果与分析

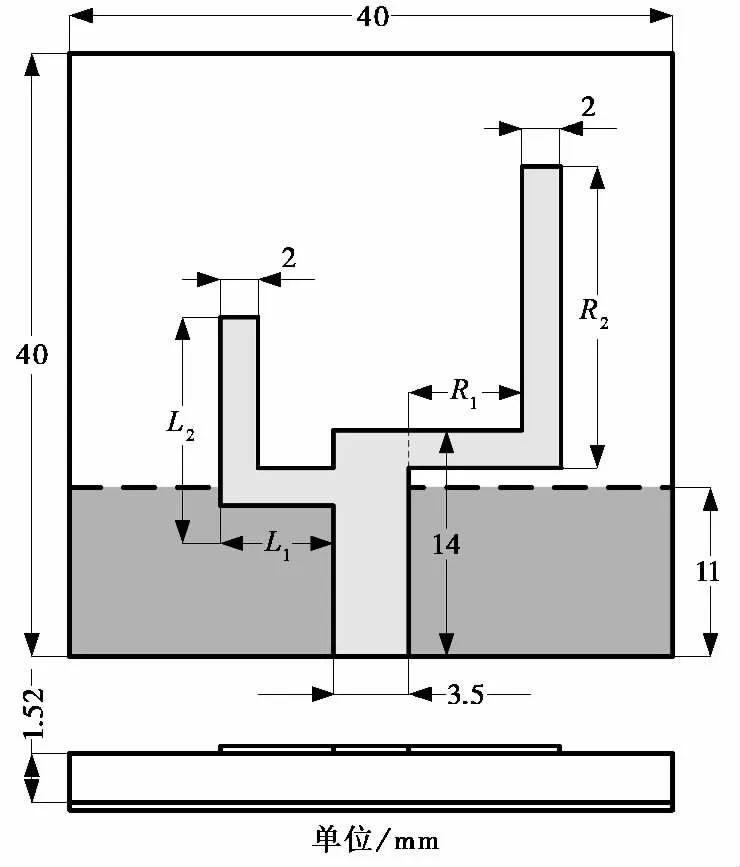
图2 天线结构图（单位：mm）

为验证有效性，使用上述算法对文献［14］中一个WLAN双频单极子天线进行优化设计，结构与尺寸如图2所示，基板材料为Rogers RO4003，介电常数εr＝3.38，损耗角正切tanδ＝0.002 7，天线由微带线馈电，左右两边各有一个L型振子，分别工作于高频段（5.15～5.825GHz）和低频段（2.4～2.483 5GHz）.设计要求为频段内S11＜-10dB，待优化参数向量为振子长度x＝（x1＝L1，x2＝L2，x3＝R1，x4＝R2）.电磁仿真由Ansoft HFSS完成，优化算法在Matlab上实现.

2.1 粗糙模型

虽然HFSS采用自适应网格剖分，不能直接控制网格数量，但可以通过设定网格剖分的最大允许误差ΔS来调整模型精度.采用3级粗糙模型，各级粗糙模型和精细模型的网格数量和平均求解时间如表1所示.

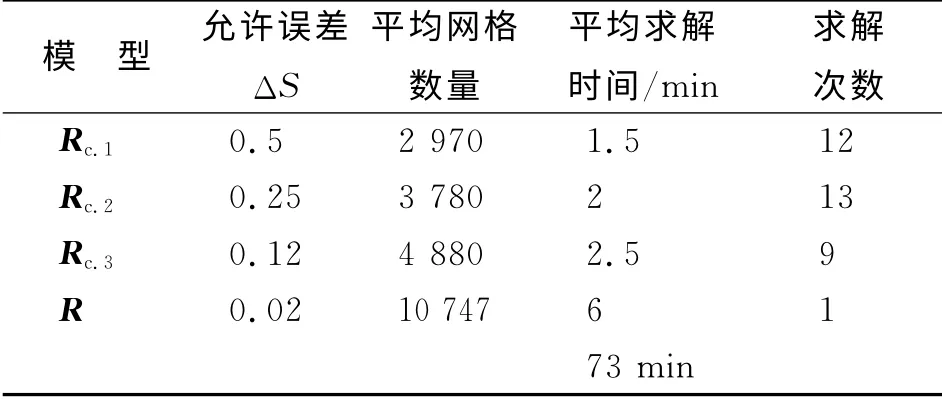
表1 多精度仿真方法计算消耗

2.2 适应度函数

由式（3）可知适应度函数值决定了对参数向量的搜索方向，因此要求其既能反映尺寸变化引起天线性能的好坏变化，又不能过于敏感以致于仿真误差影响搜索方向.由于是对阻抗带宽的优化，以频段内各频点S11来计算适应度，单个频点的适应度定义为

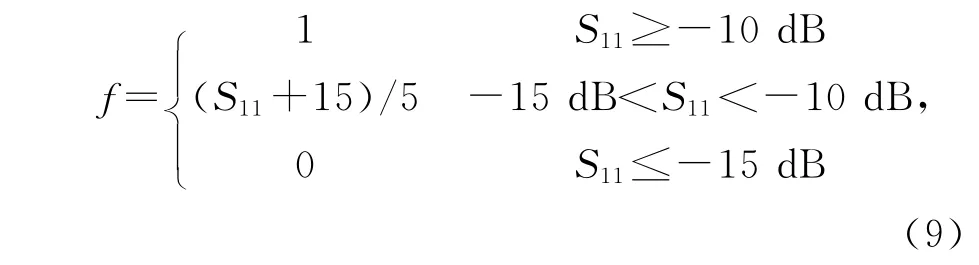
响应向量的适应度定义为

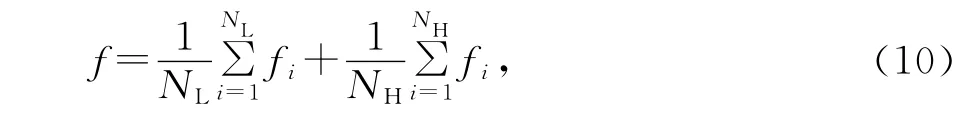
NL、NH分别为低频段和高频段的频点个数.

2.3 天线优化过程与结果分析

参数向量初始值为x（1）＝（6，9，6，19），扰动向量d（1）＝（1，1，2，2），在Rc.1优化后最优向量＝（5，9，6，19），初始参数和最优参数对应的S11曲线如图3所示.令x（2）＝作为初始值在Rc.2上以扰动向量d（2）＝（0.5，0.5，1，1）重复优化过程，最优向量＝（4.5，7.5，7，19.5），结果如图4所示.在Rc.3上，扰动向量d（3）＝（0.25，0.25，0.5，0.5），以x（3）＝x（2）op为 中 心，在［x（3）-d（3），x（3）＋d（3）］区域内拟合Rc.3（x）～x，并以V＝R（x（K））-Rc.3（x（K））对拟合结果做修正，遍历区间［x（3）-d（3），x（3）＋d（3）］，求出最优参数向量xop＝（4.5，7.7，7.4，19.8）.利用精细模型求解xop得到的S11曲线如图5所示，低频段S11＜-13dB，高频段S11＜-14dB足设计要求，图中还画出了在高、低两个频段上的S11拟合结果，可以看出与精细模型响应相比，拟合结果的误差主要为高频段的频点偏移，约为50MHz.

利用拟牛顿法以频带内S11＜-10dB为优化目标，得到最优参数向量xop＝（4.1，6.6，9.7，19.2），两种优化方法得到的S11曲线如图6所示.优化设计的计算消耗如表2所示，与表1对比可以看出采用多精度仿真方法可以显著提高优化效率.

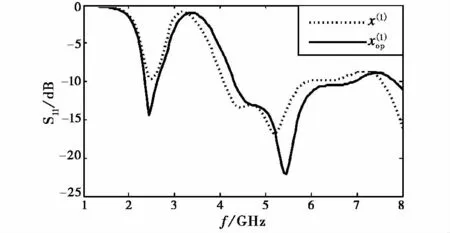
图3 Rc.1优化结果（初始值（虚线），优化后（实线））

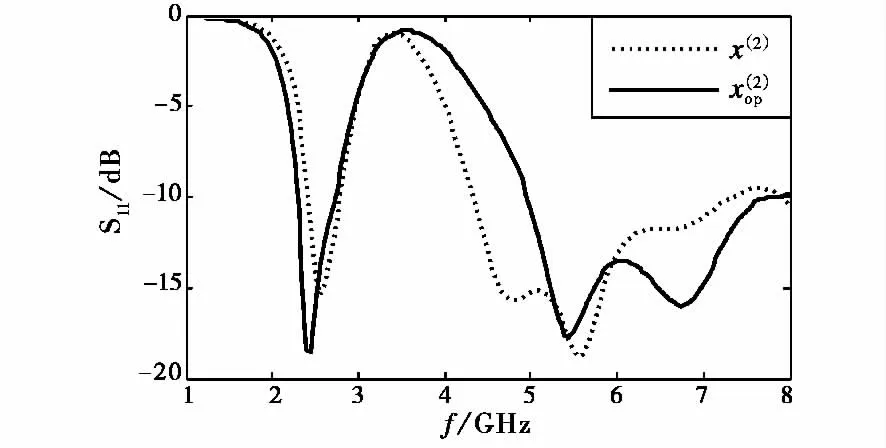
图4 Rc.2优化结果（初始值（虚线），优化后（实线））

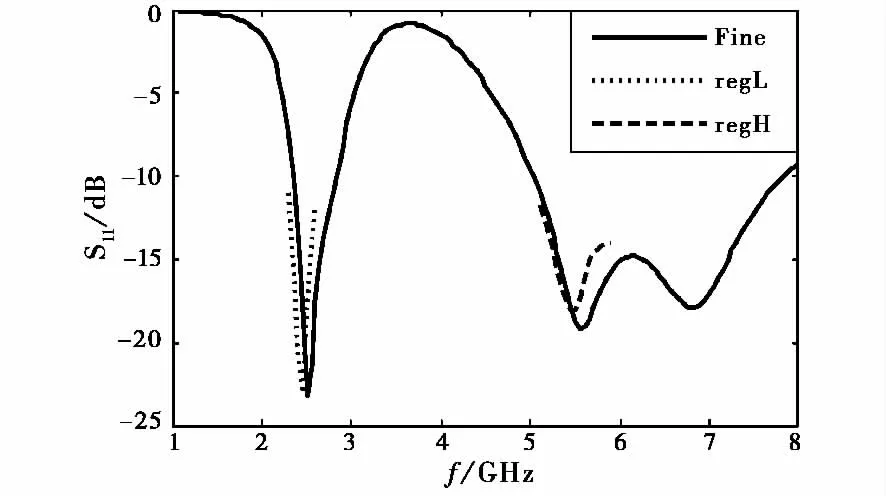
图5 精细模型上优化设计后的S11曲线（实线）与拟合曲线（虚线）

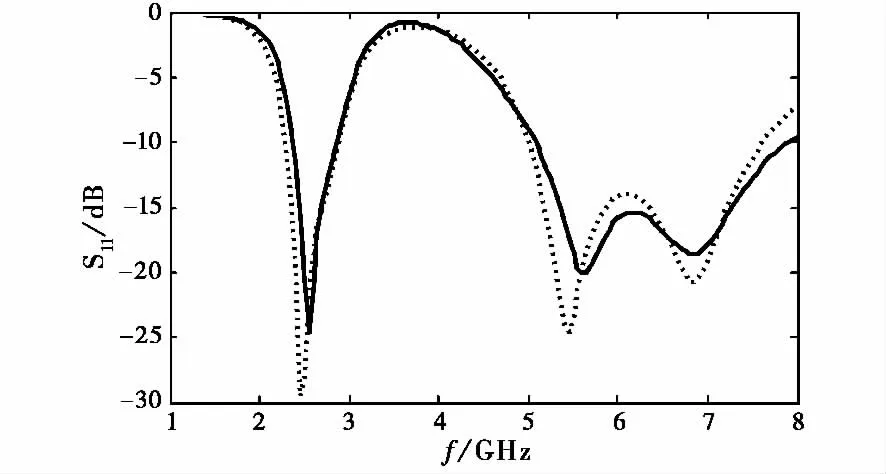
图6 优化后的S11曲线（多精度仿真方法（实线），拟牛顿法（虚线））

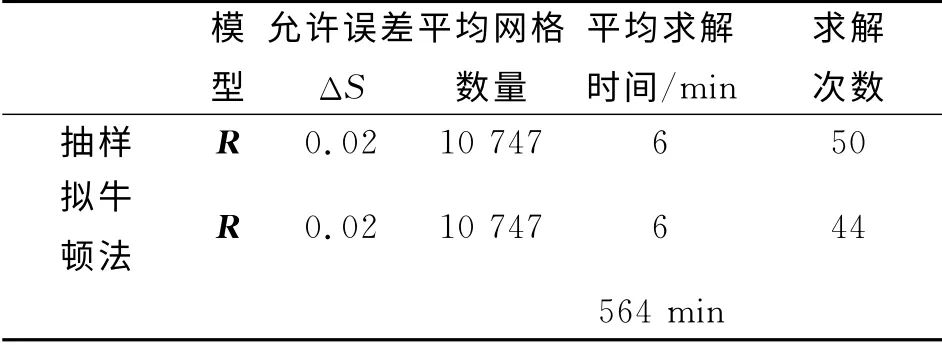
表2 拟牛顿法计算消耗

3 结 论

本文在多精度粗糙模型基础上应用区域搜索、方向搜索和拟合方法进行天线优化设计，与在精细模型上的参数扫描优化相比，提高了计算效率，节约了计算时间.但是方法的收敛性以及如何减小拟合过程中出现的误差仍然需要进一步的研究.

［1］QUEIPO N V，HAFTKA R T，SHYY W，et al.Surrogate-based analysis and optimization［J］.Progress in Aerospace Sciences，2005，41（1）：1-28.

［2］孙思扬，吕英华，张金玲，等.基于遗传算法的超宽带微带天线优化设计［J］.电波科学学报，2011，26（1）：62-66.SUN Siyang，LÜYinghua，ZHANG Jinling.Design and optimization of UWB antenna based on genetic algorithm［J］.Chinese Journal of Radio Science，2011，26（1）：62-66.（in Chinese）

［3］MENG Jicheng，XIA Lei.Support vector regression model for millimeter wave transitions［J］.International Journal of Infrared and Millimeter Waves，2007，28（5）：413-421.

［4］周金柱，黄 进，薛 欣.基于支持向量回归的腔体滤波器机电耦合建模与优化［J］.电子与信息学报，2011，33（11）：2780-2784.ZHOU Jinzhu，HUANG Jin，XUE Xin.Modeling and optimization for electromechanical coupling of cavity filters based on support vector regression［J］.Journal of Electronics ＆Information Technology，2011，33（11）：2780-2784.（in Chinese）

［5］KOZIEL S，OGURTSOV S，BAKR M H.Antenna modeling using space-mapping corrected Cauchy approximation surrogates［J］.Microwave and Optical Technology Letters，2012，54（1）：37-40.

［6］袁 军，邱 扬，刘其中，等.基于空间映射及遗传算法的车载天线优化配置［J］.电波科学学报，2006，21（1）：26-32.YUAN Jun，QIU Yang，LIU Qizhong et al.Position optimal design of vehicular antennae via space mapping and genetic algorithm［J］.Chinese Journal of Radio Science，2006，21（1）：26-32.

［7］REZAEE P，ESFAHANI N N，KNOECHEL R，et al.Active learning method for designing miniaturized waveguide filters loaded by broadside-coupled split ring resonators［C］／／13th International Conference on Electromagnetics in Advanced Applications.Torino，September 12-16，2011：1074-1077.

［8］ANURADHA，PATNAIK A，SINHA S N.Design of custom-made fractal multi-band antennas using ANNPSO［J］.IEEE Antennas and Propagation Magazine，2011，53（4）：94-101.

［9］NEOG D K，PATTNAIK S S，PANDA D C，et al.Design of a wideband microstrip antenna and the use of artificial neural networks in parameter calculation［J］.IEEE Antennas and Propagation Magazine，2005，47（3）：60-65.

［10］丁 文，王高峰，樊 绮.偶极子天线电流分布的快速分层算法［J］.电波科学学报，2008，23（5）：858-861.DING Wen，WANG Gaofeng，FAN Qi.Fast hierarchical method for current calculation of dipole antenna［J］.Chinese Journal of Radio Science，2008，23（5）：858-861.（in Chinese）

［11］GALGANI G，GUIDA G，SABBADINI M，et al.Antenna design framework：solving the EDA antinomy［C］／／5th European Conference on Antennas and Propagation.Rome，April 10-15，2011：2839-2843.

［12］KOZIEL S.Multi-fidelity multi-grid design optimization of planar microwave structures with sonnet［C］／／26th Annual Review in Applied Computational Electromagnetics.Tampere，April 26-29，2010：719-724.

［13］KOZIEL S，OGURTSOV S.Antenna design through variable-fidelity simulation-driven optimization［C］／／7th Loughborough Antennas and Propagation Conference.Loughborough，November 14-15，2011.

［14］李明洋，刘 敏，杨 放.HFSS天线设计［M］.北京：电子工业出版社，2011.