反应谱离散性对梁桥概率地震需求预计的影响

章劲松，陈 亮

（1.安徽交通职业技术学院 土木工程系，合肥230051；2.合肥工业大学 土木与水利工程学院，合肥230009）

现行的桥梁抗震设计主要通过动力时程分析来预计桥梁结构在特定地震灾害环境下的地震响应和破坏规律，特别是在地震中结构有可能进入非线性的情况下。因此，必须要选择一系列与场地地震危险性相符合的地震波作为输入地面运动，通过动力分析对结构地震需求进行预计，作为抗震设计的依据。如果所选地震波与场地的地震危险性不相符，则会使计算出的结构地震需求与实际震害大相径庭，从而导致依据地震需求进行的桥梁抗震设计无法起到应有的作用，在历次震害中这种现象均较为明显。地震环境中有很多不确定性因素会对结构地震需求产生不同程度的影响，例如地面运动、钢筋和混凝土材料、构件几何形状等的不确定性以及空间变异性等，其中地面运动对于结构地震需求的影响最为显著［1－3］。而且，随着基于性能的地震工程学（Performance－Based Earthquake Engineering，PBEE）和抗 震 设 计 理 论 （Performance－Based Seismic Design，PBSD）在世界范围内的迅速发展，地震学对于结构抗震的重要性日益凸显。

对于结构抗震而言，在地面运动的众多特性中，频谱特性、幅值和持时对于结构地震需求的影响最大。其中，频谱特性对于结构地震需求影响的研究主要集中于实际地震波的谱匹配修正技术以及人工波的拟合［4－5］，但这2种方法生成的地震波都已经改变了原始地震波的很多重要特性，而且原始地震波都是非平稳过程，特别是近场地震波的类脉冲特性、破裂方向性效应等特殊性质是人工波和谱匹配技术很难模拟的。因此，人工波和谱匹配技术的正确性在国际地震工程界一直受到质疑，且人工波和实际地震波的计算结果经常会出现显著差异。Cimellaro等［6］研究发现采用谱匹配地震波进行结构动力分析会产生过于保守的结果；而 Bhatt［7］和Demartinos［8］等则发现人工波或谱匹配的地震波会产生非保守的结构地震需求预计；美国、日本等国的一些规范如ASCE［9］等都明确规定，重要结构（如核电站等）的抗震设计必须要使用实际地震波。

针对PBEE和PBSD，频谱特性对于结构地震需求影响的研究则主要集中于原始地震波反应谱均值对于结构地震需求预计的影响［10－12］，而对于反应谱离散性的相关研究较少。但针对基于概率理论的PBEE和PBSD，反应谱离散性对于结构地震需求的影响非常显著，因为计算结果的离散度会直接影响到对于地震反应概率分布的预计［13］，从而影响到概率地震需求模型、地震易损性曲线等一系列计算结果的精确性。如果在PBEE和PBSD中使用人工波，会人为地减小地震需求的离散度，使地震需求中出现大值和小值的概率减小，改变了地震需求的概率分布，在计算结果中引入明显的偏差［14］。针对上述问题，笔者主要探讨原始实际地震波的反应谱离散性对于桥梁结构概率地震需求预计的影响，从而为PBEE和PBSD的实施过程中实际地震波的合理选取提供重要依据。

1 桥梁结构模型及其动力特性

选择某高速公路上1座三跨预应力混凝土连续箱梁桥（跨径组合：3×30m）作为算例，其总体布置见图1。算例桥梁采用直径为1.8m的圆形独柱式实心钢筋混凝土桥墩，固定墩设置在1号墩，其余各墩、台在纵桥向均采用板式橡胶支座，墩高均为10m，桥台为桩柱式桥台；所有承台均为矩形实体式，下配直径1.2m的钻孔灌注桩。

图1 算例桥梁的立面布置图

算例桥梁有限元模型的建立和动力分析均采用美国太平洋地震工程研究中心（PEER）的专业地震反应分析软件OpenSees［15］来实现。对于非线性有限元模型（见图2），主梁采用弹性梁柱单元模拟；桥墩采用基于位移的非线性梁柱单元模拟，并将桥墩截面离散成未约束混凝土纤维单元、核心混凝土纤维单元和钢筋纤维单元，同时考虑P Δ效应［10］。纵桥向的板式橡胶支座采用零长度单元模拟，并采用双线性的恢复力 位移模型；采用零长度单元模拟土弹簧来考虑土 结构相互作用［16］。

图2 算例桥梁的非线性有限元模型

模态分析表明，在纵桥向和横桥向均只有一阶模态的质量参与系数贡献显著，故无明显的高模态效应，可以更加清晰地分析地震波反应谱的离散性对于梁桥结构地震需求的影响。算例桥梁动力特性具体见表1，表中只列出了纵桥向和横桥向几阶主要模态的计算结果。

表1 算例桥梁的动力特性

针对梁桥结构中主要的滞回耗能构件，也是最易损的构件：桥墩和支座，采用墩顶漂移比和支座最大位移［10，17－18］作为桥梁结构地震需求参数，在PBEE和PBSD中称之为工程需求参数（Engineering Demand Parameters，EDP），分别用来表征桥墩和支座的最大变形能力（位移EDP）。由于在纵桥向固定墩受力和变形均最大，因此在纵桥向，EDP主要考虑固定墩的墩顶漂移比和桥墩处的支座最大位移；由于算例桥梁为对称结构，在横桥向，EDP主要考虑固定墩的墩顶漂移比。

2 地震波反应谱的离散性对桥梁结构概率地震需求预计的影响

2.1 实际地震波的选择

在纵、横桥向分别选择质量参与系数最大的一阶模态周期谱加速度作为地面运动强度参数（Intensity Measure，IM），即Sa（T1＝0.68s）和Sa（T2＝0.44s），来表征工程场地的地震活动性。选择2个地震波库（Bin1和Bin2）用于动态增量分析（Incremental Dynamic Analysis，IDA）［19－20］。 将Bin1和Bin2所选地震波的反应谱在2个关键周期即T1＝0.68s和T2＝0.44s处分别调整到0.2 g，其几何平均值谱和反应谱离散度曲线见图3。在概率统计分析中对于反应谱和EDP的概率预计采用计算数据的几何平均值来衡量，离散度采用计算数据自然对数的标准差来衡量［18］。

在纵桥向和横桥向，质量参与系数最大的一阶模态周期分别为T1＝0.68s和T2＝0.44s，比较接近，因此，将2个Bin所选地震波在T1和T2周期处的谱加速度分别调幅到0.2 g后，对比分析图3（a1）和（b1）可知，2个Bin的几何平均值谱的匹配情况也较为接近。总体看来，2个Bin的几何平均值谱匹配较好，特别是在T1和T2附近的反应谱区段，但在T＞2.0s区段内2个Bin的几何平均值谱出现一些差异。

图3 几何平均值谱和反应谱离散度曲线

对比分析图3（a2）和（b2）可知，调幅后，在T＜T1和T＜T2范围内2个Bin所选地震波的反应谱离散度比较接近；但在T≥T1和T≥T2范围内，两个Bin所选地震波的反应谱离散度则明显是Bin2＞Bin1。

对于无高模态效应的梁桥结构，在不同桥向，大于等于质量参与系数贡献最显著的一阶模态周期处的反应谱（例如对于算例桥梁纵桥向，T≥T1＝0.68s范围内的反应谱）对于结构地震反应影响最为显著［10］。因此，通过2组实际地震波在调幅后反应谱离散度的显著差异，详细分析对结构地震反应影响显著的区段内的反应谱离散性对于梁桥结构概率地震需求预计的影响。

2.2 纵桥向计算结果分析

分析图3（a1）和图4（a1）、（a2）可知，由于 Bin1和Bin2的几何平均值谱在T≥T1＝0.68s的区段内匹配较好，故2个Bin计算所得固定墩纵桥向墩顶漂移比和支座纵桥向最大位移的几何平均值IDA曲线均较为接近，即EDP概率预计基本一致，特别是随着地面运动强度的增加，一致性更加明显。

图4 由Bin1和Bin2计算所得算例桥梁纵桥向EDPs的几何平均值IDA曲线和离散度曲线

通过进一步对比分析还可以发现，在纵桥向，墩顶漂移比IDA曲线的匹配程度要稍好于支座最大位移IDA曲线；Bin2的计算结果略大于Bin1。这主要是因为，随着地面运动强度的增加，结构的非线性程度不断提高，结构基本周期T1不断延长，由于在0.68s≤T1＜1.0s区段内，Bin2的几何平均值谱略大于Bin1；在1.0s≤T1＜2.0s区段内，2个Bin的几何平均值谱基本一致。对于按规范设计，具有一般延性水平的桥墩，纵桥向基本周期可能的延长范围在（2.0～3.0）T1（即1.36～2.04s）之间，故0.68s≤T1＜2.0s区段内的几何平均值谱对纵桥向位移EDP起到了控制作用［10］。

对比分析图4（b1）、4（b2）与图3（a2）可知，在2个Bin纵桥向计算结果的几何平均值基本一致的情况下，Bin2对于纵桥向位移EDP概率预计的离散度均明显小于Bin1，且随着地面运动强度的增大，离散度曲线之间的差异也越发显著。这主要是因为在0.68s≤T1＜1.5s区段内，2个Bin地震波反应谱的离散度较为接近，特别是在T1附近的反应谱；在T1≥1.5s区段内，Bin2的反应谱离散度明显大于Bin1，且离散度差异呈现出不断增大的趋势。因此，随着地面运动强度的增加，T1延长的速度会不断加快，很快进入到T1≥1.5s区段内，从而造成2个Bin计算结果的离散度差异也在不断增大。

进一步对比可以发现，2个Bin计算所得EDP离散度曲线之间的差异与T1≥0.68s区段内反应谱离散度曲线之间的差异具有较高的近似性，充分说明T1≥0.68s区段内的反应谱离散度对于纵桥向位移EDP的离散度起到了控制作用。

2.3 横桥向计算结果分析

分析图5（a）和图3（b1）可知，对于算例桥梁，Bin1和Bin2计算所得固定墩横桥向墩顶漂移比的几何平均值IDA曲线依然较为接近，且2条IDA曲线的变化趋势与2个Bin几何平均值谱的变化趋势保持了较好的一致性，具有较为明显的相关性。

分析图5（b）和图3（b2）可知，由于在T≥T2范围内，Bin2所选地震波的反应谱离散度明显大于Bin1，从而导致Bin2在不同地面运动强度水下对于横桥向位移EDP概率预计的离散度均明显大于Bin1，使其计算精度和效率大为降低。

综上所述，从概率统计意义上来说，对于连续梁桥结构，无论是纵桥向还是横桥向，所选地震波的反应谱离散性对于桥梁结构EDP的概率预计（几何平均值）及其离散度影响显著，反应谱离散度越大可能会引起更大的结构地震需求离散度。因此，在没有高模态影响的情况下，选择合理的实际地震波，在对结构地震反应影响显著的反应谱区段内（如T≥T1），如果可以尽可能减小所选地震波的反应谱离散度，则能够显著提高对于结构EDP概率预计的精确性和计算效率。

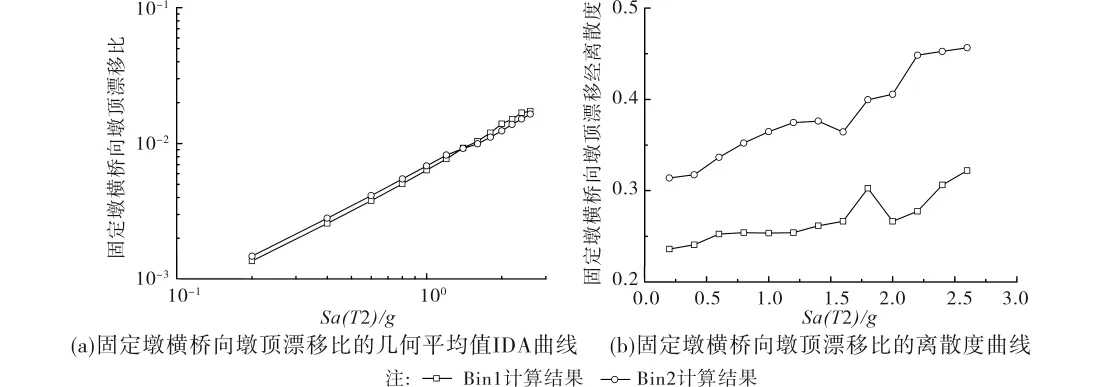
图5 由Bin1和Bin2计算所得横桥向EDP几何平均值IDA曲线和离散度曲线

采用谱匹配技术进行处理的实际地震波或人工波进行动力分析所得的计算结果，虽然离散度较小，但由于处理过的地震波改变了原始地震波的许多重要地震动特性，这种离散度的减小是不符合实际情况的，会使EDP样本中出现大值和小值的概率减小，从而改变了EDP的概率分布，对概率地震需求模型和地震易损性曲线等分析结果产生显著影响，可能会在计算结果中引入明显的偏差。因此，针对基于概率理论的PBEE和PBSD，应尽可能采用原始的实际地震波作为输入地面运动进行动力分析，谨慎使用经过处理的实际地震波或人工波。

3 结 论

以一座高速公路三跨规则预应力混凝土连续梁桥作为实例，选择频谱特性具有一定差异的2组实际地震波作为输入地面运动，采用专业地震反应分析软件OpenSEES为该桥建立有限元模型，并通过IDA分析探讨地震波反应谱的离散度对于桥梁结构概率地震需求预计的影响，可以得到以下结论：

1）实际地震波的反应谱离散度与桥梁结构概率地震需求预计的离散度密切相关，具有一定的正比关系；在连续梁桥无高模态的情况下，对于纵桥向和横桥向，分别在T≥T1和T≥T2区段内的反应谱离散度对结构位移地震需求预计的离散度影响显著（T1和T2分别为纵、横桥向质量参与系数最大的一阶模态周期）；

2）随着地震动强度和结构非线性程度的不断提高，反应谱离散性对于结构地震需求的影响逐渐减小，特别是接近破坏或倒塌时；

3）选择合理的实际地震波，在对结构地震反应影响显著的区段内尽可能减小反应谱之间的离散性，可以合理地考虑到高模态的影响，并减小离散度放大效应等对于桥梁结构概率地震需求预计的影响，提高对于均值预计的精确性和计算效率。

4）从概率统计意义上，实际地震波反应谱的离散性会显著影响到桥梁结构地震需求的概率分布模型，因此针对基于概率理论的PBEE和PBSD，应尽可能采用原始的实际地震波作为输入地面运动进行动力分析。

［1］Lee T－H， Mosalam K M.Probabilistic seismic evaluation of reinforced concrete structural components and systems ［R］.Pacific Earthquake Engineering Research Center，College of Engineering，University of California，Berkeley，2006.

［2］Kwon O－S，Elnashai A.The effects of material and ground motion uncertainty on the seismic vulnerability curves of RC structure ［J］.Engineering Structure，2006，28：289－303.

［3］Lee T H，Mosalam K M.Probabilistic fiber element modeling of reinforced concrete structures ［J］.Computers and Structures，2004，82（27）：2285－2299.

［4］Hancock J，Bommer J J.Using spectral matched records to explore the influence of strong－motion duration on inelastic structural response ［J］.Soil Dynamics and Earthquake Engineering，2007，27：291－299.

［5］Jun D H.Seismic response of R／C structures subjected to simulated ground motions compatible with design spectrum ［J］.The Structural Design of Tall and Special Buildings，2013，22：74－91.

［6］Cimellaro G P，Reinhorn A M，D'Ambrisi A，et al.Fragility Analysis and seismic record selection ［J］.ASCE Journal of Structural Engineering，2011，137（3）：379－390.

［7］Bhatt C，Bento R.Comparison of nonlinear static methods for the seismic assessment of plan irregular frame buildings with non seismic details［J］.Journal of Earthquake Engineering，2012，16（1）：15－39.

［8］Demartinos K， Faccioli E.Probabilistic seismic performance assessment of classes of buildings using physics－based simulations and ground－motion prediction equations ［J］.Journal of Earthquake Engineering，2012，16（1）：40－60.

［9］American Society of Civil Engineering.Seismic design criteria for structures，systems，and components in nuclear facilities［S］.ASCE／SEI 43－05，Reston，VA，2005.

［10］陈亮，李建中.地震波的反应谱谱形对RC梁桥结构非线性地震反应的影响［J］.工程力学，2011，28（10）：86－92，110.Chen L，Li J Z.The influence of response spectral shape of earthquake ground motions on nonlinear seismic responses of reinforced concrete girder bridge structures［J］.Engineering Mechanics，2011，28（10）：86－92，110.

［11］Haselton C B，Baker J W.Accounting for ground motion spectral shape characteristics in structural collapse assessment through an adjustment for epsilon［J］.ASCE Journal of Structural Engineering.2011，137（3）：332－344.

［12］Catalan A，Benavent－Climent A，Cahis X.Selection and scaling of earthquake records in assessment of structures in low－to－moderate seismicity zones ［J］.Soil Dynamics and Earthquake Engineering，2010，30：40－49.

［13］Baker J W.Conditional mean specrum：a tool for ground motion selection ［J］.ASCE Journal of Structural Engineering，2011，137（3）：322－331.

［14］Baker J W，Vector－valued ground motion intensity measures for probabilistic seismic demand analysis［D］.Stanford：Stanford University，2005.

［15］OpenSEES ［OL］.http：／／OpenSEES.berkeley.edu，2012.

［16］Kunnath S K.Application of the PEER PBEE Methodology to the I－880Viaduct ［R］.Pacific Earthquake Engineering Research Center，University of California，Berkeley，2007.

［17］Kevin M，Bozidar S.Seismic demands of performancebased design of bridges ［R］.Pacific Earthquake Engineering Research Center，College of Engineering，University of California，Berkeley，2003.

［18］Shome N， Cornell C A， Bazzurro P，et al.Earthquakes，records and nonlinear responses［J］.Earthquake Spectral，1998，14（3）：469－500.

［19］Vamvatsikosa D，Cornell C A.Applied incremental dynamic analysis ［J］.Earthquake Spectra，2004，20（2）：523－553.

［20］Vamvatsikosa D.Performing incremental dynamic analysis in parallel ［J］.Computers and Structures，2011，89（1／2）：170－180.