建筑物中多点支撑管道系统地震反应谱计算方法

国 巍，余志武，王永泉

（1.中南大学 土木工程学院，长沙410075；2.高速铁路建造技术国家工程实验室，长沙410004；3.河海大学 水利水电学院，南京210098）

近几年来，随着我国经济发展和工业化进程推进，土木建筑行业进入飞速发展阶段，一方面是建筑物主结构（primary system）体型日趋大型化和复杂化，另一方面建筑物内部附属仪器设备、管道系统等子结构（secondary system）日趋增多，成为实现建筑物功能的重要组成部分，与建筑物主结构共同构成主 子 结 构 体 系 （primary－secondary systems）。1989年美国加州Loma Pirta地震、1995年日本神户地震和1999年台湾集集地震等历次地震的经验早已证明：传统抗震设计方法难以保障建筑物内部子结构不发生损坏或仍能保持正常功能。网络控制中心、核电站、医院和大型商场等建筑物内部子结构的地震损坏所造成的损失远大于建筑物主结构引发的损失。Tagghai等［1］指出在商业建筑中子结构通常占总造价的65%～85%。一条普遍适用的规律是：现代化和工业化程度越高则子结构损坏所引发损失在总损失中占据的比例也越大。因此，土木工程抗震设计不仅要关注建筑物主结构，同时还要对仪器设备、管道系统等子结构进行抗震性能评估和合理设计，这也是当前世界范围内普遍推行和发展的基于性能抗震设计理念的重要内容。

主 子结构体系地震响应的早期研究主要集中于20世纪80、90年代欧美国家核电和化工等工业领域，许多国际知名学者做出了卓有成效的研究成果，并引领着该领域的发展。进入21世纪，研究更侧重于建筑物进入弹塑性状态时子结构地震响应，较具代表性的为 Villaverde［2］、Politopoulos等［3］和Sankaranarayanan等［4］的研究工作。相比而言，中国此方面研究则较少，李杰等［5］、秦权等［6］最早进行了相关方面的较具代表性的数值和试验研究。曾奔等［7］研究了隔震结构的楼板反应谱计算方法。李忠献等［8］结合大亚湾核电站实际工程进行了反应堆厂房楼板反应谱分析和评估。国巍等［9］阐述了考虑多维地震和平扭耦联效应的楼层反应谱特征。黄金连［10］指出非结构构件抗震性能现有评价指标的不足并加以改进。综合前人研究可知，相比单点支撑仪器设备等子结构而言，管道系统承受空间耦合力作用，地震响应更为复杂，计算方法以Afura和Kiureghian所提出的互 互楼层谱方法［11］（Cross－Oscillator Cross－Floor Response Spectrum，CCFS）为人们所普遍接受。然而，互 互楼层谱方法是基于位移输入模型所推导，决定了其无法计算管道系统支撑附近自由度相对位移，这点类似于大跨结构地震分析的多点反应谱方法［12］。如果试图利用管道系统与建筑物之间连接单元的精细划分来克服此缺陷，则会因位移模型固有问题［13］导致底部单元内力计算上的显著误差且计算量大幅增加。

在前人研究成果的基础上，本文依据虚拟激励法推导并修正了互 互楼层谱方法的基本理论，建立了建筑物中管道系统地震响应求解的反应谱统一计算公式，克服了互 互楼层谱方法的缺陷，可以实现管道系统支撑附近自由度的相对位移求解，最后通过数值算例验证了本文方法的有效性，并解释阐述了其应用范围。采用本文所提出和改进的反应谱方法，可以计算建筑物内管道系统在结构层面的地震响应，进而可依据结构计算结果实现管道系统在构件层面的设计和评估，如管道材质选取、截面和构造细节设计等。利用本文方法，通过对大量多种工况的系统深入研究，可对建筑物内管道系统抗震设计提出普适性的指导建议，这正是本文所提出和改进方法的重要价值和意义所在。

1 理论推导

建立建筑物上多点支撑管道系统的一般模型，如图1所示。假定建筑物有nS个自由度，管道系统有nP个自由度，建筑物与管道系统相连的自由度数为ns，即管道系统存在ns个支撑，将建筑物上此ns个自由度分别归于建筑物主结构和管道系统，并以刚臂连接。

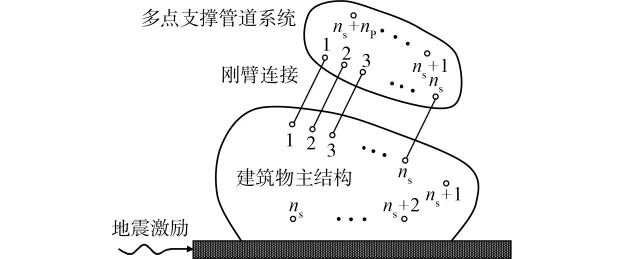
图1 地震激励下建筑物上多点支撑管道系统模型示意图

依据图1中自由度分区，定义建筑物主结构的绝对位移响应为U ＝ ［Us，］T，其中Us和分别为建筑物中刚臂连接和非连接自由度响应，类似定义管道系统的绝对位移响应为u＝ ［us，］T，其中us和分别为管道系统中刚臂连接和非连接自由度响应，易知Us＝us。单向地震加速度激励下建筑物主结构和管道系统子结构动力平衡方程可分别写为：

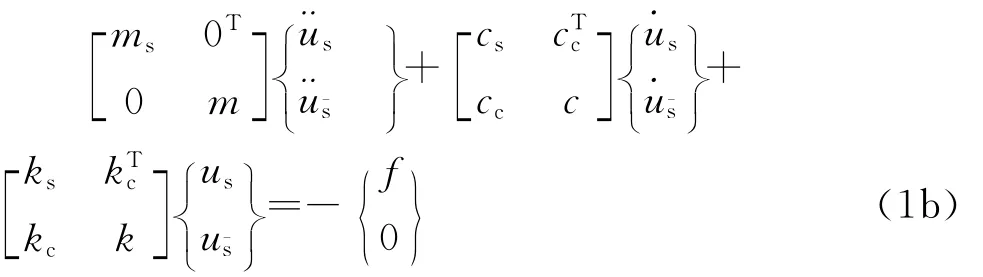
其中：M、C和K分别为建筑物的质量、阻尼和刚度矩阵；E为位移影响向量，表征地面单位静位移时建筑物上各自由度位移；m、c和k分别为管道系统的质量、阻尼和刚度矩阵；cc和kc分别为管道系统与建筑物的耦合阻尼和刚度矩阵；ms、cs和ks为刚臂连接自由度的质量、阻尼和刚度矩阵；力向量f表征建筑物与管道系统之间的相互作用。利用式（1b）可得到对应管道系统自由度的动力平衡方程：

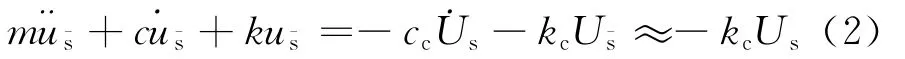
其中，Us是建筑物上支撑处各自由度位移；式（2）中忽略交叉阻尼－cc，正是基于多点激励位移输入模型，当底部单元不精细划分或不采用隔震设计时，式（2）结果足够精确［12］。

1.1 管道系统随机响应

管道系统属于位移敏感型子结构，建立管道系统各自由度相对位移表达式具有实际意义。定义管道系统的圆频率ωi、阻尼比ζi和模态φi＝［φ1i，φ2i，…，］T，i＝1，2，…，n，计算中一般取（≤PnP）阶模态即可。令建筑物主结构上支撑自由度响应为Us＝ ［Us1，Us2，…，Usn］T，即存在ns个支撑点

s并对应建筑物上s1，s2，…，sns自由度，自功率谱为基于林家浩提出的虚拟激励法［14］，构造ns个虚拟响应：

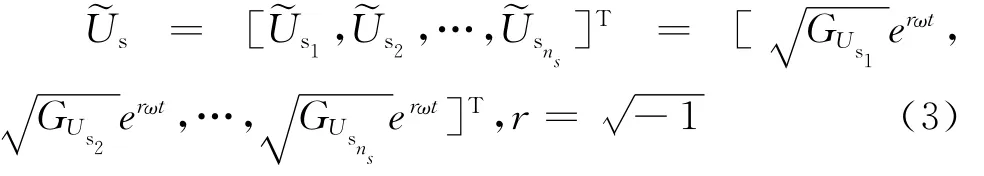
管道系统第z（1≤z≤nP）个自由度绝对位移响应可写为如下形式：

其中，mi＝mφi，频率响应函数hi（ω）＝（－ω2＋为矩阵kc的第k列向量，为向量为k个元素。为简化上述表达式，定则式（4）可改写为：

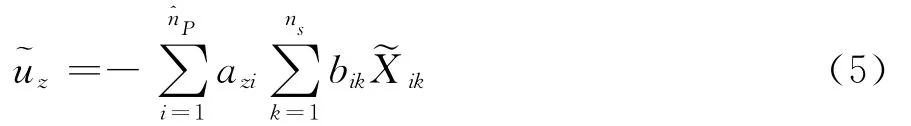
其中，ez为管道系统位移影响向量e的第z个元素；位移影响向量e表征建筑底部发生单位静位移时管道系统的位移。同时，由于上式可进一步写为：

其中，azi、bik为上文定义系数，ik为ik体系中虚拟振子对于地面的相对位移，为管道系统第z个自由度对于地面的相对位移。

1）管道系统内部自由度

管道系统内部自由度之间相对位移以及与其有关的反应量Rs（In），如内力等，可以由位移向量˜v求得：

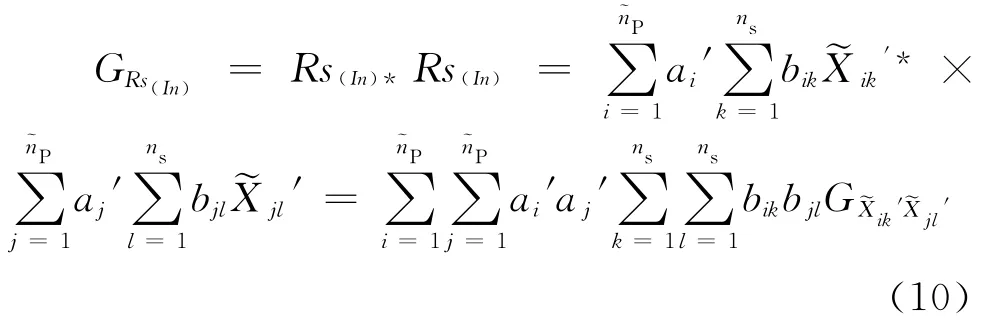
对上式两边积分可得到反应量Rs（In）均方值的表达式为：

2）管道系统支撑处自由度

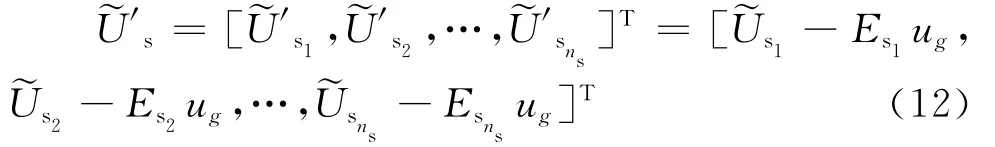
继而，令管道系统ns个支撑点附近自由度的位移响应表达式为p2，…，pns≤nP，则管道系统第o（1≤o≤ns）个支撑附近自由度相对建筑物位移可写为：

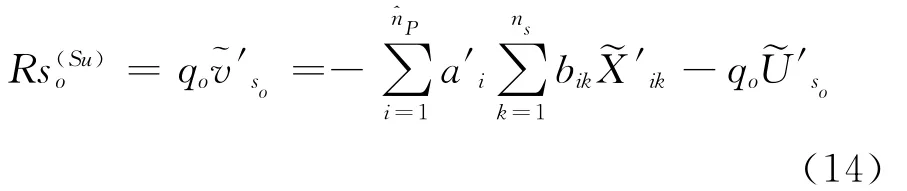
其中，qo为几何、材料常系数管道系统第o个支撑附近自由度的反应量Rs功率谱可写为：

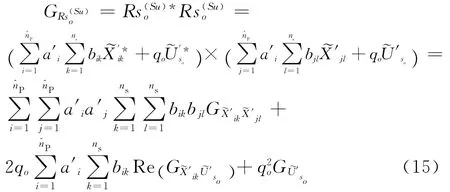
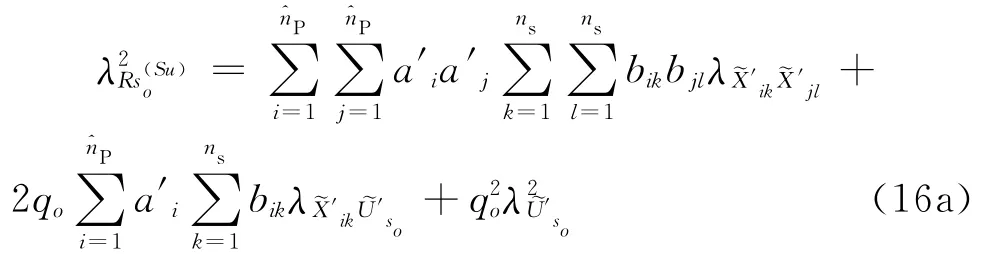
1.2 虚拟结构体系随机响应

由上文推导可见，建筑物上管道系统地震响应求解需采用式（11）和式（16），二者均需求解虚拟ik、jl体系和建筑物第so个自由度的响应。

1）ik和jl结构体系

ik和jl结构体系由建筑物和一个虚拟振子所组成，虚拟振子依据质量、频率、阻尼比和位置来确定。本文基于近似方法求解ik结构体系的随机虚拟响应。首先，考虑主子结构之间的动力耦合效应，确定虚拟振子质量。定义建筑物主结构频率为Ωi′，阻尼比 为 Zi′，模态为 Φi′＝ ［Φ1i′，Φ2i′，…，ΦnSi′］T，1≤i′≤nS，计算中一般取（≤nS）阶模态即可。Igusa和Kiureghian［15］给出了当子结构第i阶频率与主结构第i′阶频率完全调谐时，主结构第i′阶频率偏移的计算公式，并以此确定建筑物第sk个自由度上虚拟振子质量mik表达式［11］，如下：

其次，考虑建筑物主结构与虚拟振子所构成体系的非比例阻尼特征，得到此虚拟体系的动力特征参数。定义建筑物上第sk个自由度上存在质量mik、频率ωi和阻尼比ζi的虚拟振子，此体系为ik体系。定义参数如下：

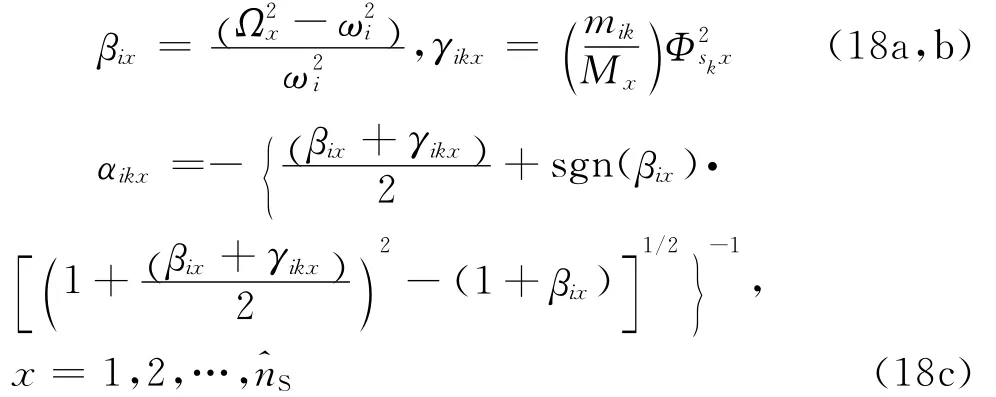
其中，Mx＝MΦx。进一步，可得到建筑物主结构和虚拟振子所构成结构的＋1）模态表达式，如下：

当建筑物主结构第i′阶与虚拟振子频率接近时，即Ωi′≈ωi时，体系第i′阶模态向量为：

ik结构体系各阶频率可写为如下形式：

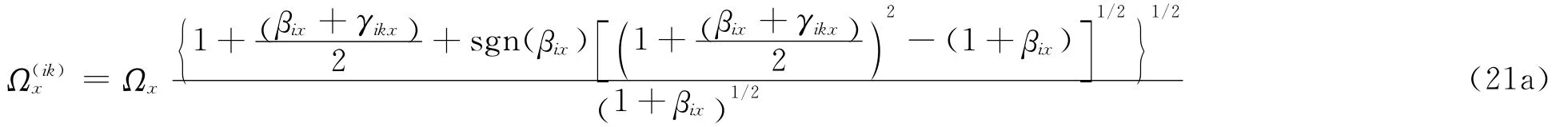
为了解释非比例阻尼特征，认为当建筑物频率与虚拟振子频率非调谐时当建筑物频率与虚拟振子频率调谐或接近调谐时，即Ωi′≈ωi时，采用下式定义：

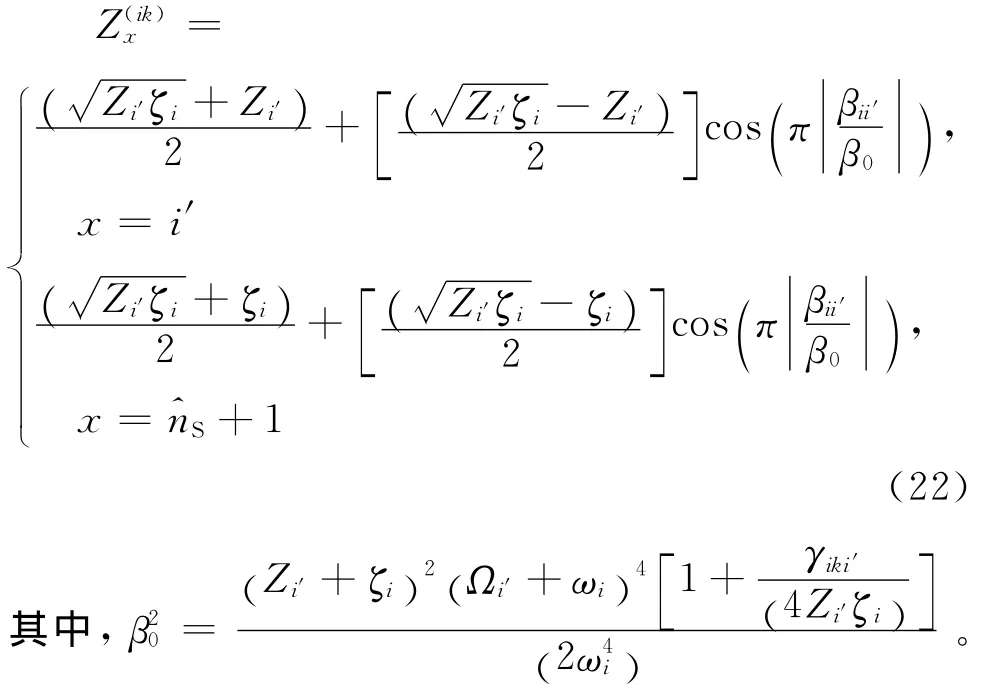
由以上所给公式可得知ik和jl结构体系的动力特征参数，进一步可得到地震激励下结构虚拟随机响应′ik和′jl：

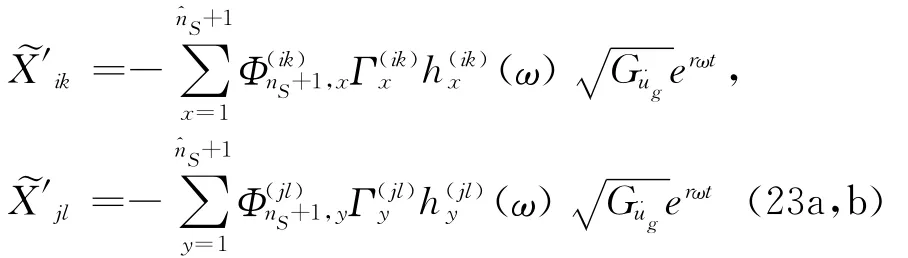
从而可计算ik和jl结构体系中虚拟振子的响应功率谱，如下：

式（24）两边积分可得如下表达：

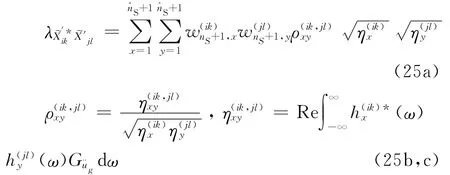
2）无管道建筑物结构

本文此处考虑到建筑物上管道系统质量往往较轻，当小于建筑物质量的1%时，即便存在某阶频率的调谐共振，建筑物所受影响也相对较小，此时可近似忽略管道系统对建筑物的影响。建筑物主结构第o个支撑处自由度的随机虚拟响应可写为：

从而可计算ik结构体系虚拟振子与无管道建筑物的响应功率谱，如下：

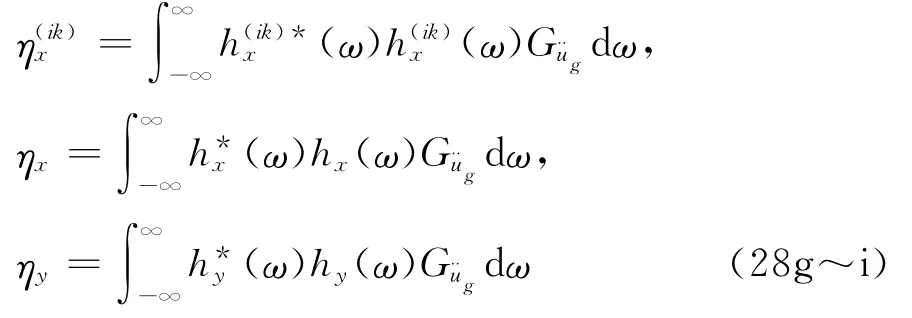
其中，ηx（ηy）为无管道建筑物第x（y）阶模态自由度的随机响应均方值。利用式（16）和（28）可计算管道系统支撑附近自由度相对位移随机响应，这点是互－互楼板谱方法所无法实现的。

1.3 反应谱组合公式

如上文推导所示，建立了管道系统内部自由度和支撑附近自由度的随机响应均方值表达式，即式（11）、式（16）、式（25）和式（28）。假定不同随机过程的极限因子均相同，依据所推导的随机响应公式，则管道系统Rs（In）和Rs反应谱计算公式为：

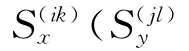
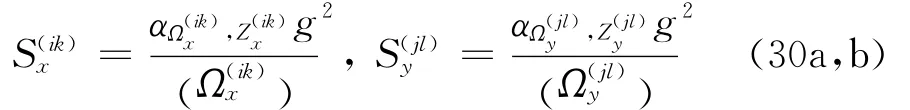
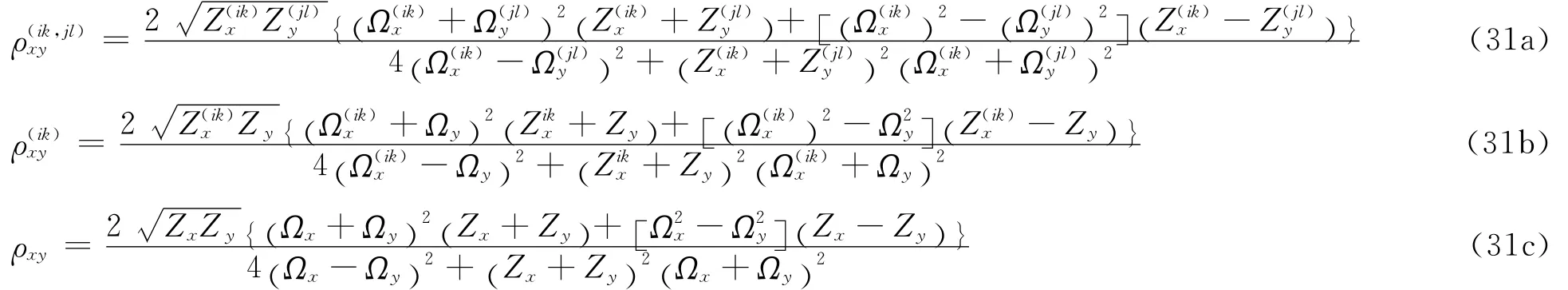
至此，建立起了管道系统基于地面反应谱的完整且统一的计算公式，即（29a，b），并且给出了式中相关系数的简化计算方法，即式（31a～c）。所建立的反应谱计算公式对管道内部自由度和支撑附近自由度分别推导，修正和完善了互 互楼层谱方法，主要体现在其不仅可求解管道系统内部自由度，同样可以准确求解支撑附近自由度的相对位移，这点是传统互 互楼层谱方法所无法做到的。同时，对于主 子结构体系的动力耦合效应，推导中根据实际情况有所区别的灵活对待。首先考虑到建筑物管道系统质量往往较轻，不论频率调谐共振与否，建筑物所受影响都较小，为减小计算量采用无管道建筑结构响应来参与计算，而对于计算中所构造虚拟振子计算中则采用摄动法考虑动力耦合和非比例阻尼。需要说明的是，所提方法和传统互 互楼板谱方法均需要进行6次连加∑运算，计算量远远大于反应谱分析的CQC方法。如仅从计算效率考虑，此时采用虚拟激励法进行随机运算，往往更具计算优势［16］，在某些情况下虚拟激励法已可取代反应谱方法。然而，鉴于随机振动理论掌握起来较为困难且往往难以说明非平稳地震响应特征，当前土木工程抗震设计中仍然主要采用设计反应谱方法，本文所提出的方法具有重要的工程实际意义。

2 数值算例

建立由建筑物与管道系统所组成的主 子结构体系模型，如图2所示。地震激励采用El－centro和Taft地震波，并依据7度抗震设防小震调整其加速度峰值至0.35m／s2，图3给出了El－centro和Taft地震波调幅后时程曲线和对应反应谱曲线。图2所示建筑物主结构参数为：各层质量均为mS＝1×105kg，各层间刚度均为kS＝2×104kN／m，阻尼则定义为Rayleigh阻尼，其前两阶模态阻尼比为0.05。由于是进行方法验证，且关注建筑物中管道系统在结构层面的地震响应，这里直接给出管道系统的质量、刚度、阻尼等结构动力参数，而并不具体到管道细部，如材料和截面等。子结构质量从小到大，相应参数取值为：各质点质量均为mP＝αmS，其中α＝［0.000 1，0.001，0.01，0.05］，对应各种不同质量工况。管道系统各连接刚度均为kP＝βmP，其中β＝［32.22，80，160］，β决定了管道系统的频率特征，当β＝32.22时主子结构基频完全一致，体现调谐共振，当β＝［80，160］时主子结构体现非调谐。定义支撑处固定的管道系统前两阶模态阻尼比为0.02。

图2 地震激励下建筑物 管道系统示意图

图3 El－centro和Taft地霸记录的时程和反应谱

图4 El－centro和Taft地震激励下管道系统相对位移响应基于耦合和解耦方法求解结果对比

首先分别采用耦合和解耦方法计算在不同质量情况下管道系统地震时程响应，并进行对比研究。取管道系统系统的1～5质点之间相对位移及1，3，4质点相对于所支撑楼层的位移为研究对象，定义指标：DP＝［d1，d2，d3，d4，d5，d6，d7］＝［质点1－楼层1，质点2－质点1，质点3－质点2，质点3－楼层3，质点4－质点3，质点5－质点4，质点5－楼层5］。绘制在不同质量比、不同频率情况、不同求解方法和不同地震输入下各指标变化情况，结果绘于图4。从图4中可以看到，当管道系统质量较小时，解耦处理是可行的，其精度接近耦合计算结果，体现在图4中为mP＜0.001 mS时解耦与耦合曲线几乎重合。当mP＝0.01 mS时，频率调谐时的解耦计算精度下降，会得到较为保守结果，但并不过于保守，当频率非调谐时解耦计算精度仍然较好，这是规范规定当子结构质量小于主结构1%时可采取解耦运算的主要原因。而当mP＝0.05 mS时，不论频率调谐与否，解耦计算结果误差都较为明显，特别当调谐时解耦计算结果误差非常限制，甚至达到100%以上，此时解耦运算会导致过于保守的计算结果。因此可认为动力耦合对管道系统影响明显，在本文推导中也采用近似方法考虑了主子结构之间的动力耦合。

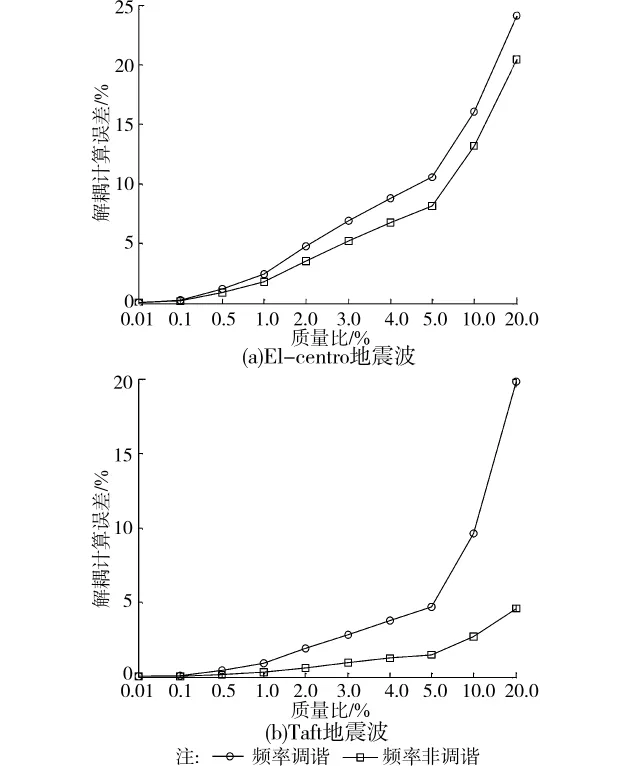
图5 El－centro和Taft地震激励下建筑物楼层5基于解耦方法计算结果误差

继而，研究不同质量比情况下采用解耦方法计算建筑物主结构响应的误差，鉴于管道系统与建筑物基频调谐影响较大，可取建筑物楼层5相对地面位移为研究对象，并定义误差为i＝1，…，nP，其中ui，c和ui，d分别为耦合计算、解耦计算所得管道系统第i自由度相对位移。图5给出了随着质量比mP／mS变化解耦运算结果的误差曲线，可以看到当mP／mS较小时不论频率调谐与否解耦方法的误差都很小，此时计算建筑物结构响应可不考虑管道系统动力反馈影响，这正是本文推导中采用无管道建筑物主结构响应的根据。

采用本文所建立管道系统反应谱方法计算管道系统各自由度相对位移响应DP，即式（29），管道系统频率kP＝80 mP，对比时程计算结果，地震动同样采用El－centro和Taft地震波。图6给出了计算结果对比曲线，可以看到不论是管道系统内自由度还是支撑附近自由度，采用本文方法都可以计算，并以时程计算结果为精确解作为对比，可以看到本文方法具备一定精度。然而类似于反应谱CQC方法，本文方法同样具有存在小范围误差，一方面是由于地震白噪声随机输入假定，另一方面是由管道系统频率分布特征所致。此外还可看到，小质量情况下管道系统质量比变化对计算结果准确性影响不大。

图6 本文方法与耦合计算方法的计算结果对比

为详细研究本文所提方法（包括互 互楼层谱方法）的计算准确度，质量特征采用mS＝ ［0.001，0.01］mP，以研究质量影响；同时变动管道系统的频率特征参数β，以研究不同频率分布影响，鉴于管道设计中往往避免与建筑物主结构基频调谐共振，此处取kP／mP＝β＝［80，160］；地震波采用El－centro和Taft地震波，以研究白噪声假定可行性。所研究的误差指标选取其中ui，c和ui，p分别为耦合计算、本文方法计算所得管道系统第i自由度相对位移。图7给出了依据本文方法在管道系统不同质量、不同频率分布和不同地震激励的计算结果的误差情况。可以看到，在不同的频率分布下本文方法（包括互 互楼层谱方法）计算结果存在不同的误差分析，且可能误差会较大，这主要是由于前文推导中建立虚拟振子体系时采用了管道系统各频率不密集分布的假定，这在实际中可能并不满足，此时基于本文公式所得结果精度也随之下降；在不同地震激励下，误差同样区别明显，这说明白噪声假定会引入一定误差，为得到更为精确结果则需采用更合适的随机模型来计算相关系数；不同质量比，对本文方法误差影响较小。

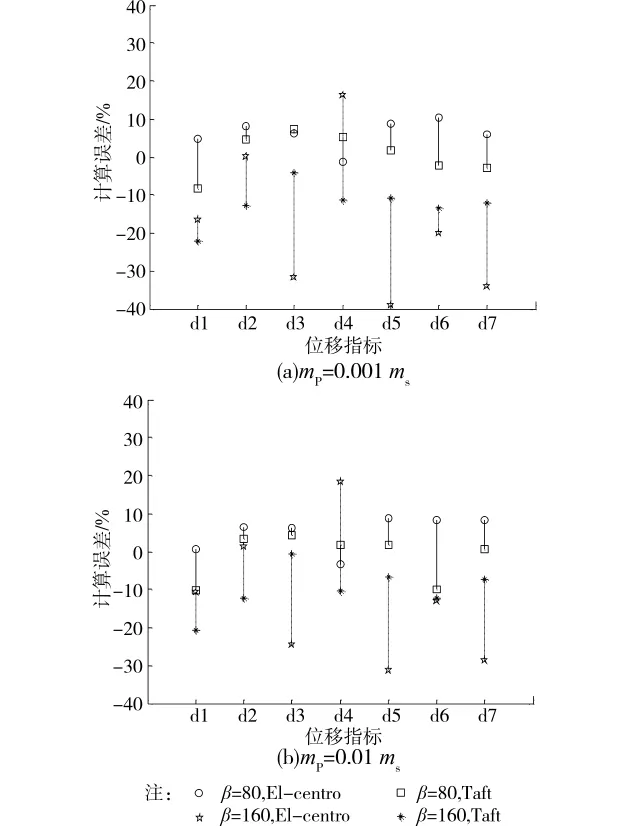
图7 基于本文所提方法计算管道系统位移指标响应结果在不同工况下的误差

3 结 论

通过理论推导指出了前人所提出的互 互楼板反应谱方法存在一定缺陷，其难以准确计算多点支撑管道系统与建筑物连接处自由度的相对位移响应，进而对理论基础加以改进并重新推导建立了多点支撑管道系统反应谱统一计算公式。通过本文研究可得到以下结论：

1）所提方法完善了互 互楼层谱方法，是互互楼层谱方法更为全面的表达形式，二者建立的理论体系相同，精度相同。

2）本文方法适用于建筑物中管道系统响应求解，在管道系统质量较轻、频率分布松散情况下会具有较为良好的精度。

3）地震激励不同同样会影响本文方法以及互互楼层谱方法的计算精度，为得到更精确结果，需要重新计算实际随机地震模型下的相关系数。

4）本文方法实现了管道系统基于规范地震影响系数的简单反应谱组合运算，便于实际工程应用，同时基于结构层面的反应谱计算结果可推至构件层面内力特征，继而开展管道材料、截面、构造措施等抗震设计和评估。

［1］Miranda E，Taghavi S.Towards the prediction of seismic performance of nonstructural elements ［C］／／Proceedings of 2003SEAOC Convention， Squaw Valley，CA，September 2003.

［2］Villaverde R.Simple method to estimate the seismic nonlinear response of nonstructural components in buildings［J］.Engineering Structures，2006，28（8）：1209－1222.

［3］Politopoulos I，Feau C.Some aspects of floor spectra of 1DOF nonlinear primary structures ［J］.Earthquake Engineering and Structural Dynamics，2007，36：975－993.

［4］Sankaranarayanan R，Medina R A.Acceleration response modification factors for nonstructural components attached to inelastic moment－resisting frame structures ［J］.Earthquake Engineering and Structural Dynamics，2007，36：2189－2210.

［5］李杰，陈淮，孙增寿.结构 设备动力相互作用试验研究［J］.工程力学，2003，20（1）：157－161.Li J，Chen H，Sun S Z.Shaking table tests of spatial structure－equipment model systems ［J］.Engineering Mechanics，2003，20（1）：157－161.

［6］秦权，聂宇.非结构构件和设备的抗震设计和简化计算方法［J］.建筑结构学报，2001，22（3）：15－20.Qin Q，Nie Y.Seismic design and simplified analytical method of nonstructural components and equipment in buildings［J］.Journal of Building Structures，2001，22（3）：15－20.

［7］曾奔，周福霖，徐忠根.隔震结构基于功率谱密度函数法的楼层反应谱分析［J］.振动与冲击，2009，28（2）：36－39.Zen B，Zhou F L.Xu Z G..Floor response spectra analysis of base－isolated structure based on PSDF ［J］.Journal of Vibration and Shock，2009，28（2）：36－39.

［8］李忠诚，李忠献.大亚湾核电站反应堆厂房楼层反应谱分析评估［J］.核科学与工程，2006，26（1）：72－78.Li Z C，Li Z X.Re－evaluation of floor response spectra of reactor building for Daya Bay NPP ［J］.Chinese Journal of Nuclear Science and Engineering，2006，26（1）：72－78.

［9］国巍，李宏男，柳国环.非线性建筑物上的附属结构响应分析［J］.计算力学学报，2010，27（3）：476－481.Guo W，Li H N，Liu G H.Seismic response analysis of secondary system mounted on nonlinear primary structure ［J］.Chinese Journal of Computational Mechanics，2010，27（3）：476－481.

［10］黄连金.非结构构件抗震性能指标及分析［D］.上海同济大学，2009.

［11］Asfura A，Kiureghian A D.Floor response spectrum method for seismic analysis of multiply supported secondary systems ［J］.Earthquake Engineering and Structural Dynamics，1986，14（2）：245－265.

［12］Liu G H，Guo W，Li H N.An effective and practical method for solving an unnegligible problem inherent in the current calculation model for multi－supported seismic analysis of structures ［J］.Science China：Technological Sciences，2010，53（7）：1774－1784.

［13］于德广.大跨度多支撑结构多点激励反应分析［D］.哈尔滨：哈尔滨工业大学，2006.

［14］林家浩，张亚辉.随机振动的虚拟激励法［M］.北京：北京科学出版社，2004.

［15］Igusa T，Kiureghian A D.Dynamic response of multiply supported MDOF secondary systems ［J］.Journal of Engineering Mechanics，ASCE，1985，111：20－41.

［16］Guo W，Yu Z W，Guo Z.Fast stochastic analysis for non－proportionally damped system ［J］.Mechanics Research Communications，2011，38（6）：468－470.