堆场龙门吊调度问题研究

乐美龙，殷际龙

上海海事大学 物流研究中心，上海 201306

1 引言

近年来，随着经济的快速发展和航运业蓬勃发展，集装箱运输业已成为全球运输行业的支柱，集装箱码头间的竞争日趋激烈。集装箱码头对于进出口船舶的操作大致可分为：卸载进口集装箱和装载出口集装箱。对于大多数码头来说，装卸集装箱所涉及的设备主要有以下三种，即桥吊、集卡以及堆场龙门吊，因此要提高码头效率、降低费用消耗，就需要合理安排桥吊、集卡和堆场龙门吊的工作时间。本文主要研究堆场龙门吊的合理调度问题，堆场龙门吊的调度直接影响到码头的装卸效率，对堆场龙门吊调度的研究有利于提高集装箱码头的竞争力。

由于龙门吊调度问题的重要性，有关龙门吊调度问题研究已取得一些进展。堆场龙门吊调度的研究目标大多为使集卡等待时间最短，或在自定义的时间窗内未完成的工作量最少。

Lai等人[1]和Leung[2]提出多种龙门吊调度规则，并利用仿真模型进行验证。Zhang[3]和Cheung[4]等人提出解决装卸任务事前预知的静态龙门吊调度模型。Zhang[5]等人提出了龙门吊调度问题的混合整数规划模型，并利用拉格朗日松弛思想加以优化。

Kim[6]研究了单个堆场龙门吊的最优路径问题，建立混合整数规划模型，使龙门吊在箱区总移动时间最小。Ng等人[7]提出利用分支定界法来优化堆场龙门吊调度问题。Chen等人[8]提出了堆场龙门吊调度模型，并用禁忌搜索法加以求解。Javanshir和Seyedalizadeh Ganji[9]提出了避免多龙门吊相互干扰的龙门吊调度问题模型，利用启发式算法求解并与Lingo求得的结果进行对比。

对于龙门吊调度问题，国内研究相对较少，本文通过考虑正在工作的龙门吊不能跨越等约束条件，提出龙门吊合理调度模型使集卡等待时间最小化。

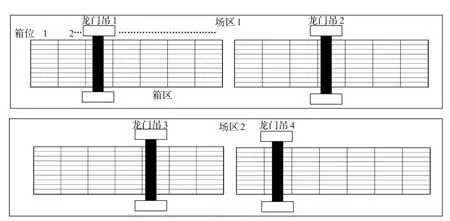
图1 堆场场区示意图

2 问题描述

堆场龙门吊调度问题是集装箱码头整体规划中的重要部分，合理、高效地调度龙门吊可以节约资源，减少能耗和提高码头操作效率，从而提高码头的竞争力。本文通过考虑龙门吊间的干扰，合理调度龙门吊，减少集卡的等待时间。图1为堆场场区示意图。

模型基于以下假设：

（1）假设每项工作的服务时间是固定的，并且每台龙门吊的工作效率相同。

（2）龙门吊从一个场区移动到另一个场区时，将浪费大量时间及能源，不考虑龙门吊在两场区之间的移动。

（3）需考虑龙门吊之间的干扰，龙门吊之间不能相互跨越。

3 数学模型

给定参数：

ri表示集卡的到达时间；

li表示工作i的到达位置；

dij表示工作 j与工作i之间的移动时间；

h表示每个工作的服务时间；

Zil∈{0,1},当Zil=1时表示工作i的到达位置在箱位l处；

M为一个无穷大数。

决策变量：

Si表示工作i的开始时间；

Di表示工作i的完成时间；

Xijk∈{0,1},当 Xijk=1时表示同一台龙门吊k对工作i的服务先于工作 j；

Ylk∈{0,1},Ylk=1时表示龙门吊k服务于箱位l。

龙门吊调度模型如下：

4 遗传算法设计

由于模型比较复杂，利用求解器求解会使求解时间过长，故本文利用遗传算法进行求解。遗传算法是一种高效的、相对成熟的智能算法，其模拟自然进化，按照适者生存和优胜劣汰的原理，逐代演化产生出越来越好的近似解，最终得到近视最优解。遗传算法的流程设计如图2所示。

4.1 染色体编码

本文中染色体编码采用实值编码，即工作序号表示染色体上的基因，用基因的先后顺序来表示服务的先后顺序。图3为染色体示意图，其表示有两台龙门吊，10个工作，第一台龙门吊服务工作{4，5，3，6，8}，第二台龙门吊服务工作{1，2，7，10，9}，其中的0将两台龙门吊的工作分隔开。

4.2 计算适应度和选择父代染色体

（1）首先利用约束条件（7）对染色体进行筛选

筛选步骤如下：

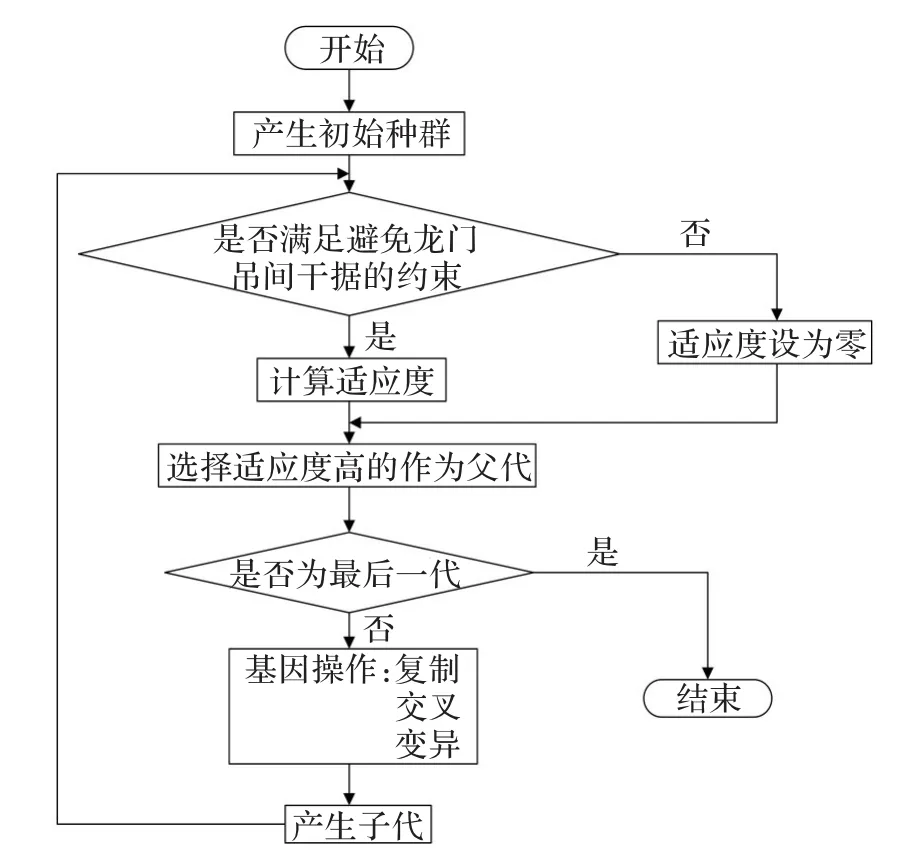
图2 遗传算法设计流程图

图3 染色体示意图

步骤1将需要服务的工作按到达时间从小到大排列。

步骤2检查每条染色体中，不同龙门吊执行的任务是否存在时间上的重合，即Di>Sj。当此种情况存在时，检查是否满足约束（7），满足则直接计算适应度进行初始父代的选择；否则将该染色体的适应度标记0。

步骤3重复步骤2，直至不存在不满足约束（7）的染色体。

（2）适应度计算

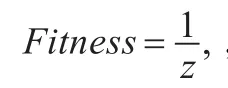
（3）选择父代染色体

采用最佳保留选择法对父代染色体进行选择，即先按轮盘选择规则（每个个体被选择的概率为其适应度占整个种群适应度的比例，比例越大被选择概率越大）执行选择操作，然后将当前群体中适应度最高的个体结构完整的复制到下一代中。

4.3 染色体交叉

染色体交叉是遗传算法的重要操作，其示意图如图4，本文采用的交叉步骤如下：

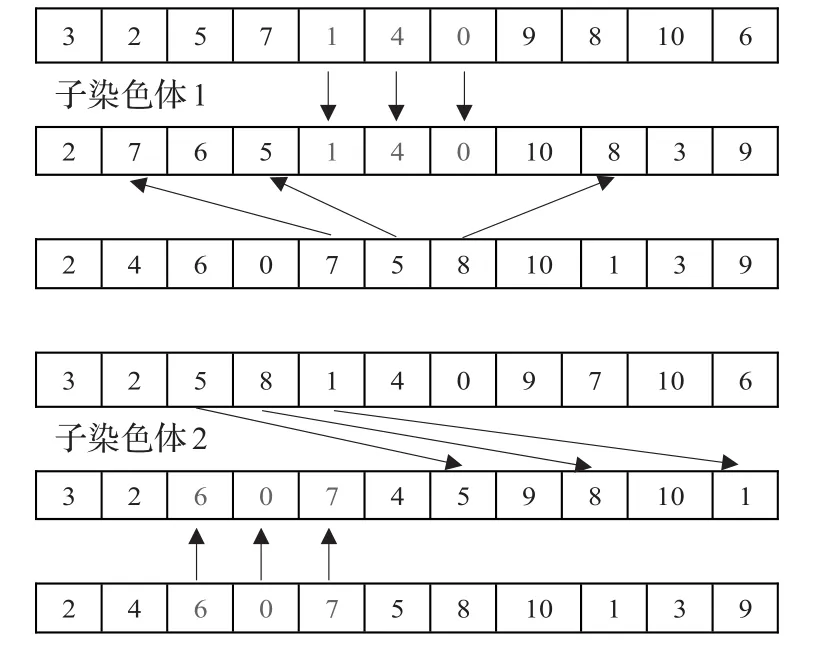
图4 染色体交叉示意图

步骤1在一个父代中随即产生一个子串。

步骤2将这个子串复制到第二个父代的相同位置，删除第二个父代中相同的基因。

步骤3将第二个父代剩余的基因从左向右顺序放入子代空位中。

4.4 变异

本文采用的是实数编码，因此在变异操作中需随机选择两个基因位置，并将其位置互换。基因的变异概率比较小，根据以往的研究数据，文中的变异概率取值为0.09。图5为基因变异示意图。

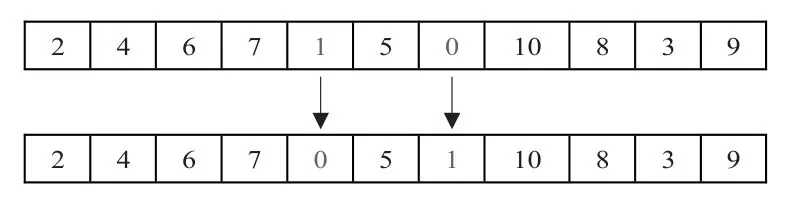
图5 基因变异示意图

5 算例

用遗传算法来计算下面这个算例。龙门吊数K=2，工作数m=10，设时段开始时间为0，每个工作都是卸载一个相同规格的集装箱并将其堆放到指定位置（或将一个集装箱装载到集卡上）。各个工作的到达时间分别为r1=60 s，r2=240 s，r3=360 s，r4=540 s，r5=660 s，r6=720 s，r7=960 s，r8=1 080 s，r9=1 260 s，r10=1 440 s；集装箱到达的箱位为l1=l4=1，l2=l6=5，l3=l5=7，l7=l10=13，l8=15，l9=19；龙门吊的操作一个集装箱用时为240 s，移动时间dij=3×|li-lj|。

利用遗传算法对算例进行求解，得到运算结果如表1所示。龙门吊1的工作顺序为1-4-6-7-10，对应的箱位为1-1-5-13-13；龙门吊2的工作顺序为2-3-5-8-9，对应的箱位为5-7-7-15-19。集卡最小等待总时长为312 s，最早完成时间为1 680 s。

表1 算例运算结果

图6为龙门吊在这10个工作时段的运动轨迹（如龙门吊1的轨迹，第一个拐点表示龙门吊1离开箱位3，第二个拐点表示龙门吊1到达箱位5），可以更为直观地看出龙门吊所处的位置以及最早结束时间。

下面与文献[9]的调度模式进行对比。文献[9]的模型为了避免龙门吊间的相互干扰，在约束中规定不同的龙门吊不能在同一箱位处工作，这样很好地避免了龙门吊间产生干扰，但同时也限制了龙门吊的可工作位置范围。下面利用文献[9]中的模型（在其基础上加入移动时间便于对比）来计算本文中的算例，图7为文献[9]的模型针对本文算例进行求解所得到的龙门吊移动轨迹图。

图6 龙门吊移动轨迹图

图7 基于文献[9]模型的龙门吊轨迹图

最终求得其最早完成时间为1 680 s，与本文模型计算的结果相同；最小等待时间是324 s，大于本文模型的结果312 s。可以看出，本文的模型比单纯考虑龙门吊空间位置干扰的模型更能提高龙门吊工作效率。

6 结论

在集装箱码头的物流作业中，堆场龙门吊调度问题是一个非常重要的环节。本文整体考虑龙门吊在时间和空间上的相互影响，其结果更加接近现实情况，有助于提高码头效率。

本文的创新点在于利用龙门吊工作时间上的重合以及空间位置约束来确定龙门吊的工作位置。一方面避免了人为规定工作时间段对龙门吊调度的影响，另一方面避免了单纯考虑空间位置的干扰而给龙门吊工作位置的选择带来更大的限制。最后，由于模型的复杂性，引入遗传算法进行求解，缩短了求解时间并得到了满意结果。

[1]Lai K，Lam K.A study of container yard equipment allocation strategy in Hong Kong[J].International Journal of Modeling and Simulation，1994，14（3）：134-138.

[2]Lai Leung J W.Analysis of yard crane deployment strategies in a container terminal[C]//Proceedings of ICC and IE Conference，1996：1187-1190.

[3]Zhang C，Liu J，Wan Y W，et al.Storage space allocation in container terminals[J].Transportation Research：Part B MethodoLogy，2003，37（10）：883-903.

[4]Cheung R K，Li C L，Lin W.Inter block crane deployment in container terminals[J].Transportation Science，2002，36（1）：79-93.

[5]Zhang C，Wan Y W，Liu J，et al.Dynamic crane deployment in container storage yards[J].Transportation Research：Part B MethodoLogy，2002，36（6）：537-555.

[6]Kim K H.An optimalrouting algorithm fora transfer crane in port container terminals[J].Transportation Science，2003，33（1）：17-33.

[7]Ng W C，Mak K L.Yard crane scheduling in port container terminals[J].AppliedMathematicalModeling，2005，29（3）：263-276.

[8]Chen L，Bostel N，Dejax P，et al.TaBu search algorithm for the integrated scheduling problem of container handling systems in a maritime terminal[J].European Journal of Operational Research，2009，181：40-58.

[9]Javanshir H，Seyedalizadeh Ganji S R.Yard crane scheduling in port container terminals using genetic algorithm[J].Journal of Industrial and Systems Engineering，2010，6（11）：39-50.