风电机组变桨距模糊遗传控制算法研究

杨清宇，张 冉

西安交通大学 电子与信息工程学院，西安 710049

1 引言

风力发电由于其清洁无污染、可再生、基建周期短及装机规模灵活等优点，受到世界各国的高度重视。众所周知，控制技术是机组安全高效运行的关键，变桨距控制系统作为风电机组控制系统的核心技术之一，对机组安全稳定运行具有十分重要的作用。

变桨距控制系统根据实际风速的变化情况来实时调整叶片的桨距角，改变气流对叶片攻角，从而改变风轮的起动转矩，使系统输出功率保持恒定。由于风电机组的非线性及较大的风轮转动惯量，使得变桨距控制存在响应滞后等缺陷，对控制策略提出了较高的要求[1-2]。

通过对变速变桨距机组的研究，国内外学者提出了很多方法对其进行控制，并取得了一定的研究成果，如PID控制技术、多变量控制、LQG控制、智能控制等。其中，PID控制器以其结构简单、稳定性好及调整方便等优点广泛应用于工业控制过程中，然而利用传统的PID控制需要建立风力发电机组的精确数学模型，考虑到空气动力学的不确定性和电力电子系统的复杂性，风力机系统的精确模型难以建立。为此，很多学者根据PID控制器及智能控制的特点将两者进行结合，提出了各种基于智能PID控制技术。文献[3-4]提出了模糊PID、模糊前馈与模糊PID相结合的变桨距控制方法，来改善单纯PID控制在变桨距控制中调整时间长、超调量大的问题。文献[5]利用桨距角参考值与桨距角实际测量值的误差e及误差微分e˙作为模糊自适应PID控制器的输入，通过不断检测误差e和误差微分e˙的值，对控制器的参数进行在线调整，使其具有良好的动态和静态性能，但确定模糊控制器的控制规则相对困难。文献[6]利用径向基神经网络（RBF-NN）控制器和多层感知器神经网络（MLP-NN）控制器对额定风速以上风轮的桨距角进行寻优，获得最佳风能利用系数和叶尖速比，并对两种控制器仿真结果进行了比较。仿真结果表明RBF NN控制器有更好的控制性能，在较高风速下能够保持功率输出在额定值附近，当有扰动输入时，可以有效地抑制扰动。文献[7]提出了一种基于数据挖掘技术、预测控制及进化计算的智能动态风机控制系统，建立了多目标模型，通过对五个不同的控制目标施加不同的权重系数达到对系统动态控制的目的。文献[8]利用多变量控制器将线性控制策略和非线性动态状态反馈转矩控制策略结合起来，以实现额定风速以上桨距角的调节，并与PID控制及LQG控制器进行比较。仿真结果表明多变量控制器在功率调整方面具有较好的性能。

本文在建立风电机组变桨距仿真模型的基础上，结合各控制方法的优缺点，给出了一种基于模糊遗传算法的风电机组变桨距控制方法，将遗传算法及模糊控制思想有机结合起来，以发电机输出功率误差及误差变化率作为系统输入，通过模糊遗传算法对PID控制器的参数进行调整，并在1.5 MW风电机组上进行了仿真测试。

2 风电机组建模

本文主要针对风电机组额定风速以上的变桨距控制进行研究，故对风电机组进行简化后主要包括风速模型、空气动力学模型、传动系统和发电机模型以及变桨距执行机构模型。

2.1 风速模型

风速模型由四个分量组成，分别为基本风、阵风、阶跃风和随机风。即：

其中，VWind为实时风速；VWB为基本风，表示风速模型的平均风速；VWG为阵风，表示在某一时刻突然变化的风速特性；VWS为阶跃风，表示风速的渐变特性；VWN为随机风，表示风速的不确定性，在本文中用白噪声加以描述。

2.2 空气动力学模型

风轮从风中获得的风能为：

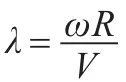
风轮气动转矩为：

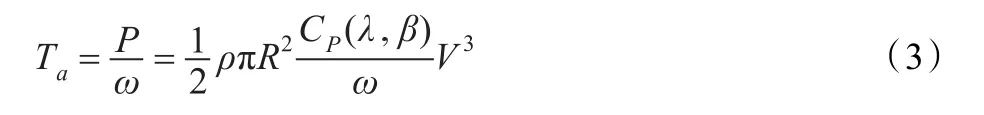
文中CP(λ,β)采用如下的经验公式：

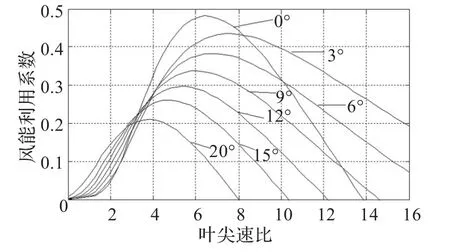
图1 风能利用系数曲线图

2.3 传动系统和发电机模型

传动系统模型由低速轴、齿轮箱、高速轴和发电机组成[8]。假定发电机和齿轮箱为刚性连接，所有的柔性都集中在低速轴，如图2所示，则系统转矩平衡方程为：

其中，Ta为风轮转动力矩；TD为能量传动的全部阻力矩；Tem为发电机的电磁转矩；ωr为风轮转速；J为风轮转动惯量，形式如下：

其中，Jr和Jg分别为风轮转动惯量和发电机转动惯量，n为齿轮箱变比。

其中，c1、c2、c3为常数。

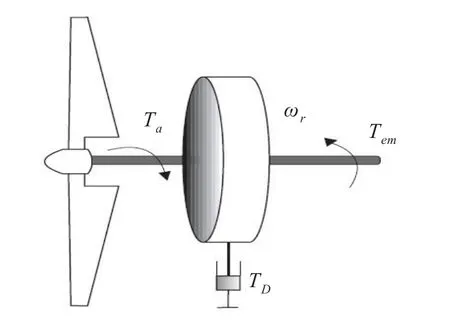
图2 风电机组传动系统模型图

2.4 变桨距执行机构模型

变桨距执行机构主要用于功率限制，是额定风速以上控制系统的核心。风速高于额定风速时，变桨距执行机构动作，桨距角增加，叶片升力系数减小，从而降低风能利用系数，达到功率限制的目的。

图3所示为变桨距系统模型[9]，其动态性能可表示为：

其中，β和βref分别为桨距角实际值和参考值，τ为时间常数。

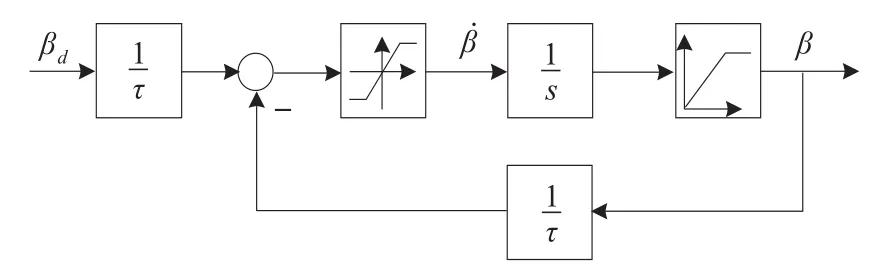
图3 变桨距系统模型图

3 模糊遗传算法

模糊遗传算法把模糊控制和遗传算法优化结合起来，从而构成一种混合优化的设计方法，目的是利用模糊优化设计的优点，克服遗传算法优化设计中所存在的收敛速度慢、计算量大等缺点[10]。其结构如图4所示。

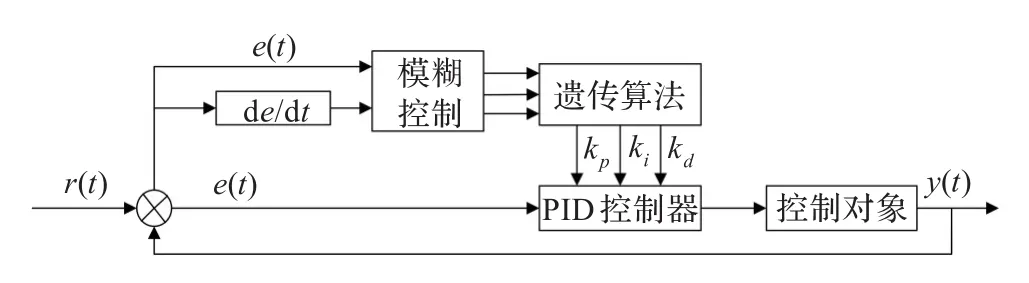
图4 模糊遗传算法结构图

本文首先利用模糊控制对系统PID控制器进行优化，从而得到一组kp、ki、kd的值，并将该组PID控制器参数值作为遗传算法的搜索内核，从而减小算法搜索时间，达到优化算法的目的。模糊遗传算法的流程图如图5所示。

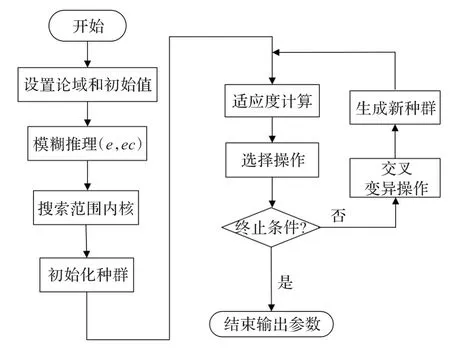
图5 模糊遗传算法流程图

3.1 参数确定

将系统误差e和误差变化率ec及控制器参数kp、ki、kd的变化范围定义为模糊集上的论域，即

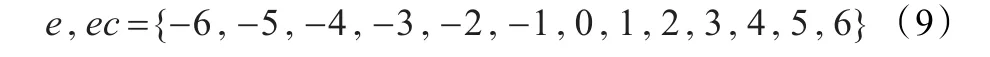
其模糊子集为e,ec={NB,NM,NS,ZE,PS,PM,PB}，子集中元素从左到右分别为负大、负中、负小、零、正小、正中、正大。控制器参数如下：

其中，kp'、ki'、kd'为当前时刻控制器的比例、积分、微分系数；kp、ki、kd为整定后控制器的比例、积分、微分系数。e、ec和kp、ki、kd均采用三角形隶属度函数，去模糊化方法采用区域重心法。

3.2 适应度函数的确定

在遗传算法中，使用适应度函数来度量接近最优解的优良程度，适应度值较大的个体进入到下一代的概率较大，而适应度值较小的个体进入下一代的概率较小。

其中，ω1、ω2为各性能指标的加权系数，代表相应性能指标所占比例，根据对系统性能的要求选定合适的参数值。考虑到适应度函数值越大进入下一代的概率越大，故选定适应度函数为：

3.3 交叉和变异

交叉是指按交叉概率从种群中选择两个个体，交换两个体的某个或某些位，从而产生新的个体。交叉运算是产生新个体的主要方法，是决定算法收敛性能的关键。交叉概率Pc越大，新个体产生速度就越快，但同时遗传模式被破坏的可能性也越大；Pc太小则会导致搜索过程缓慢，以致停滞不前，故选择自适应调整的交叉概率Pc为：

其中，kg、G分别为当前迭代次数和最大迭代次数。

变异是以较小的概率对个体编码串上的某个或某些位进行突变，避免在进化初期就陷入局部最优解而终止进化过程。变异概率Pm过小，不易产生新的个体；变异概率Pm过大，就变成了纯粹的随机搜索方法。本文采用的变异概率Pm为：

其中，S、Size分别为个体中的位和种群中的某一个体。

4 仿真结果及分析

本文以控制器的控制参数kp、ki、kd作为模糊遗传算法所要优化的个体，初始种群取为100，迭代次数为100，建立自适应调整的交叉率和变异率，防止进化过程缓慢或过早收敛于局部最优解。

将上述模糊遗传算法在1.5 MW风电机组上进行仿真测试。图6和图7分别为遗传算法和模糊遗传算法代价函数曲线。从图中可以看出，随着进化代数的增大，代价函数值逐步减小，即适应度函数值逐渐增加，进化过程趋于稳定。基于模糊遗传算法的代价函数在进行到第25代时进化终止，适应度函数达到最大值，相比于遗传算法的第63代进化结束，明显提高了收敛速度。

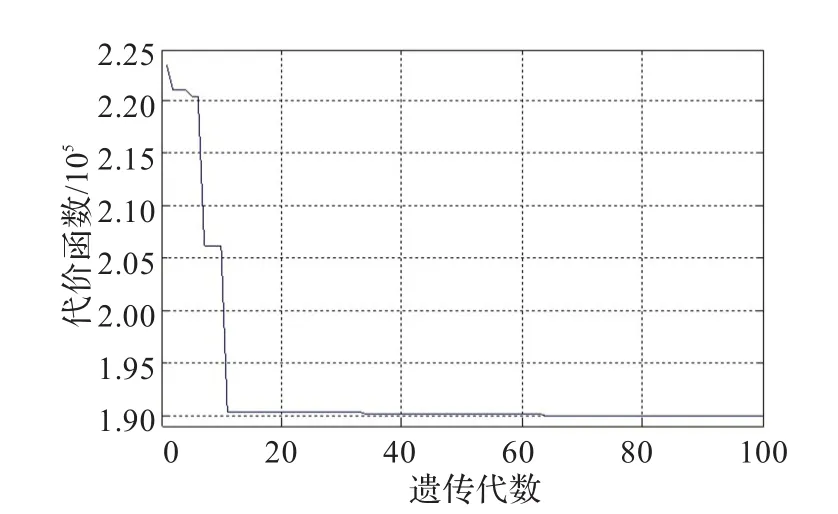
图6 遗传算法代价函数曲线图

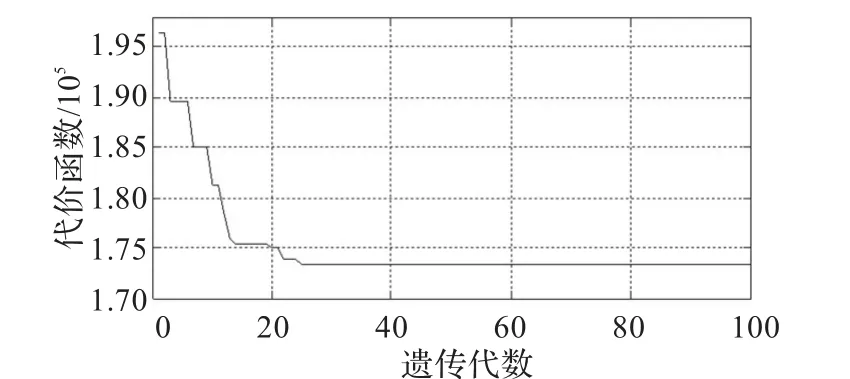
图7 模糊遗传算法代价函数曲线图

图8为模糊遗传算法和遗传算法在阶跃风速条件下的功率响应曲线。在10 s时，风速由11 m/s变化到12 m/s，由图中可以得出，模糊遗传算法在稳定性、调节时间及误差累积等方面均优于传统的遗传算法。

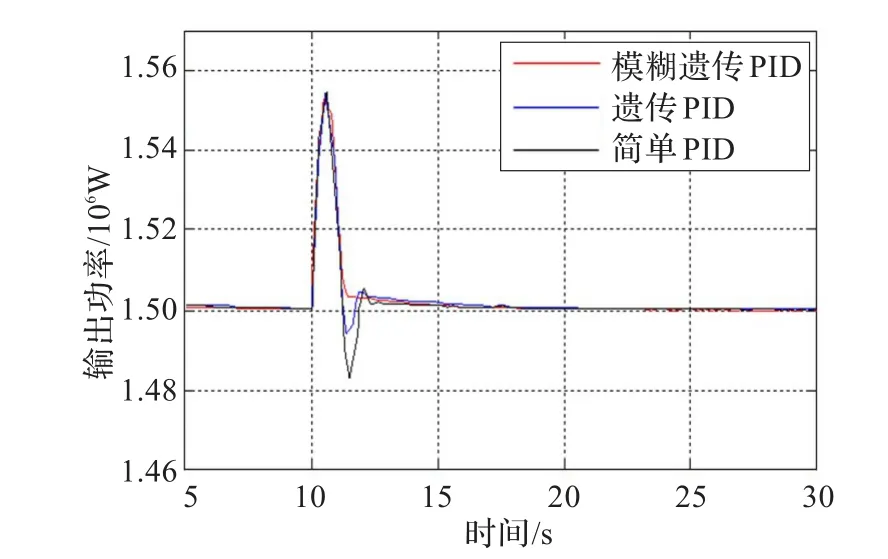
图8 功率响应曲线比较图

图9为随机风速信号条件下桨距角、发电机转速及发电机输出功率随风速变化的响应曲线。从图中可以看出，随着风速的增加或减小，桨距角也相应增加或减小，而发电机转速和输出功率都在其额定值附近波动，满足风电机组运行控制的要求。

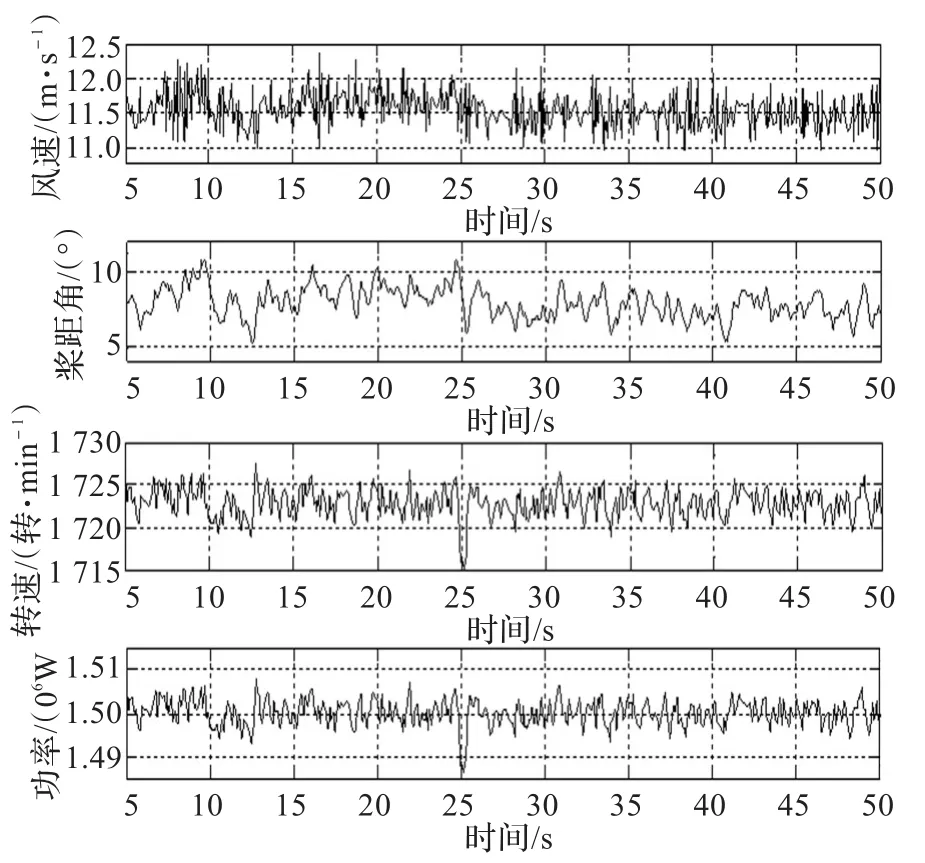
图9 随机风速条件下各信号响应曲线图

图10为同一随机风条件下发电机输出功率在不同算法条件下的响应曲线图，（a）为遗传算法条件下功率响应曲线，（b）为模糊遗传算法条件下功率响应曲线。由图中可以看出，模糊遗传算法条件下，发电机输出功率响应曲线在误差累积及系统稳定性方面均优于遗传算法。

5 结束语

本文以1.5 MW风电机组为例，将模糊遗传算法应用于变桨距控制中。仿真结果表明，在高于额定风速时的功率限制过程中，采用模糊遗传算法不仅解决了遗传算法收敛速度慢的缺点，且在系统动态性能和稳定性方面均优于传统的遗传算法，较好地满足了风电机组在额定风速以上环境的运行要求，确保了机组输出功率的稳定。

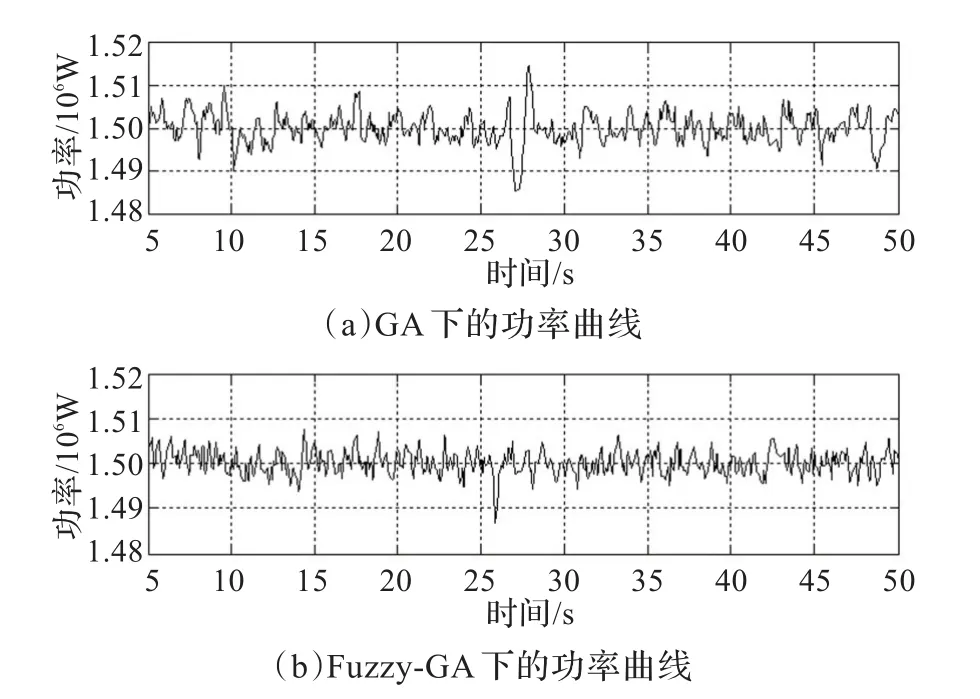
图10 遗传算法与模糊遗传算法的功率输出曲线图

[1]Muyeen S M，TakahashiR，MurataT，etal.A variable speed wind turbinecontrolstrategy to meetwind farm grid code requirements[J].IEEE Trans on Power Systems，2010，25（1）：331-340.

[2]刘军，何玉林，李俊，等.变速变桨距风力发电机组控制策略改进与仿真[J].电力系统自动化，2011，35（5）：82-86.

[3]姚兴佳，温和熙，邓英.变速恒频风力发电系统变桨距智能控制[J].沈阳工业大学学报，2008，30（2）：159-162.

[4]郭鹏.模糊前馈与模糊PID结合的风力发电机组变桨距控制[J].中国电机工程学报，2010，30（8）：123-128.

[5]Dou Z L，Cheng M Z，Ling Z B，et al.An adjustable pitch control system in a large wind turbine based on a Fuzzy-PID controller[C]//Proceedings of International Symposium on Power Electronics Electrical Drives Automation and Motion，2010：391-395.

[6]Ahmet S Y，Zafer O.Pitch angle control in wind turbines above the rated wind speed by multi-layer perception and radial basis function neural networks[J].Expert Systems with Application，2009，36（6）：9767-9775.

[7]Kusiak A，Li W Y，Song Z.Dynamic control of wind turbines[J].Renewable Energy，2010，35（2）：456-463.

[8]Boukhezzar B，Lupu L，Siguerdidjane H，et al.Multivariable control strategy for variable speed variable pitch wind turbines[J].Renewable Energy，2007，32（8）：1273-1287.

[9]Camblong H.Digital robust control of a variable speed pitch regulated wind turbine for above rated wind speeds[J].Control Engineering Practice，2008，16（8）：946-958.

[10]Qi J G，Liu Y X.PID control in adjustable-pitch wind turbine system based on Fuzzy control[C]//Proceedingsof the 2nd International Conference on Industrial Mechatronics and Automation，2010：341-344.

[11]Huang H S.Distributed genetic algorithm for optimization of wind farm annual profits[C]//Proceedings of the 14th InternationalConference on Intelligentsystem Applications to Power Systems，2007：1-6.