基于遗传粒子群算法的飞行冲突解脱

崔莉薇，石为人，刘祥明，吴文政

重庆大学 自动化学院，重庆 400030

随着民航运输事业的高速发展，空中交通流量不断增加，为了改善日益拥挤的空中交通状况，国际民航界提出了“自由飞行”的概念，所谓自由飞行就是指说驾驶员可以选择最合适的飞行路线和飞行速度进行飞行。在自由飞行环境下，航路拥挤问题将得到改善，但航路结构限制的取消，使得航空器间冲突问题的解决将变得异常复杂，管制员的工作也将变得更加复杂困难。自由飞行条件下的冲突探测与解脱近年来成为空中交通管理领域的一个研究热点。

各国的研究人员进行了大量冲突解脱算法的研究工作。ALLIOT[1]论述了基于遗传算法的解脱方法，该算法可以获得最短航迹的无冲突飞行方案，但当飞机数目增多时计算比较复杂、耗费时间多。Durand[2]运用简单的神经网络来解决两机间的冲突，可以得到满意的结果，但当冲突的飞机多于两架时，神经网络拓展十分困难，三机比两机的学习结构适应性差，而且三机以上的拓展使神经网络的规模增加，学习更困难。Ghosh[3]采用势能法解决飞行冲突，算法简单，计算速度快，但该算没有考虑解脱航迹长度与燃油消耗等因素，且随着飞机架数的增加，可能会规划出不适合实际飞机航行的航迹。国内对飞行冲突解脱的研究也取得了一定的成果，尝试应用了线性规划法[4]、模拟退火遗传算法[5]、自适应遗传算法[6]等方法解决飞行冲突解脱问题，这些方法各有特点，并取得了一定效果。本文在参考国内外有关文献和的基础上，采用一种遗传粒子群算法解决多机的飞行冲突解脱问题，并与文献[6]和粒子群算法的规划结果进行了比较。

1 问题的描述与建模

本文根据我国的空管安全规定，对多机冲突解决问题进行简化[7]：

（1）由于民用飞机一般除了在起飞和降落阶段外，都是在固定的高度飞行，且考虑到乘客的舒适要求和燃油消耗要求，飞机之间在改变航路以避免冲突时，只是在水平面内改变方向。因此可以把三维立体问题简化为二维平面问题。

（2）现实飞行中，民用飞机特别是民用运输机是一种非高机动性能飞机，且飞机在高空巡航飞行时速度无太大变化，因此假设飞机的飞行速度不变。

（3）按照我国的空管安全规定，当两架飞机之间间隔大于20 km时不存在飞行冲突。本文为提高冲突识别的准确性，采用10 km作为飞机移动的步长。

（4）民用飞机在巡航阶段正常飞行时，一般没有大角度转弯或转向飞行，且固定的航向改变使飞行员能够更好地执行冲突解决方案，并减少反应时间。这里假设飞机在飞行中任何位置只能选择3个飞行方向，即保持原有航向、左转30°、右转30°。

（5）避免冲突时，通过筛选路径最短和飞行延误最小的航路来实现最省油，也最省时。

在以上的前提条件下，假设有N架飞机同时进入一个正方形的冲突区，飞机不作任何航向调整时，保持直线飞行，飞离冲突区的点，称之为理论上的退出点。算法把飞机在冲突内的飞行时间分为K步，在每一步中，飞机保持一定的航向。在进入每一步时，飞机进行航线调整，以避免发生冲突。

约束条件为冲突区内任意两架飞机之间的距离D大于飞行安全间距δ：

航线的改变不可避免地会造成飞行路径长度的增加，飞机飞离冲突区时偏离理论上的退出点。因此，本文的优化目标有两个，分别是在保证不发生飞行冲突的情况下，使飞机的总航线长度最短且飞行延误最小（飞行延误是指每架飞机的理论退出点与实际退出点之间的距离）。

两个目标函数如下：

其中，Si为第i架飞机在冲突区内飞行路径的长度，di为第i架在冲突区内的延误。

本文使用线性加权法确定评价函数，线性加权法是最简单、最基本，也是应用最广泛的多目标优化方法。

对每架飞机根据其进入冲突解脱域的入口点，起始航向和每一步的航向变化，计算其整个航迹，并检查初始种群生成的实验航迹是否存在飞机冲突。如果发现飞行冲突，该个体的适应值将设置为0。如果没有冲突，对每一架飞机i,计算其在空域内飞机的总航线长度和飞行延误，并使用线性加权法确定评价函数。

适应值函数如下：

其中，n为冲突区内的飞机数量，di为第i架的飞行延误，Si为第i架飞机在冲突区内的飞行路径长度，k1和k2为常数。

为简单起见采用二进制编码，如果在空域里有N架飞机，则将构造一个N×K×2维的解空间，将每个个体对应的解空间，分解成N个K维向量：Xn=( )xn1,xn2,L,xnk(k=1,2,…,K)，表示第k架航班在冲突区内的航线调整。其中：

通过合理的数学建模，将多机的冲突解脱问题简化为带约束的整数规划问题。

2 基于遗传粒子群算法的飞行冲突解脱

2.1 标准遗传算法（SGA）

标准遗传算法（Simple Genetic Algorithm，SGA）是Holland于20世纪60年代提出一种计算模型[8]，它是模拟生物在自然环境中的遗传和进化过程形成的一种全局优化概率搜索算法。对于一个特定的问题，遗传算法从代表问题可能潜在解集的一个种群开始，种群由经过基因编码的一定规模的个体组成，之后按照适者生存和优胜劣汰的竞争原理，在每一代，采纳了自然进化模型，根据问题域个体的适应度大小选择优良个体，并借助自然遗传学的遗传算子进行组合交叉和变异，逐代进化以产生代表新的解集的种群。周而复始，反复迭代，直到满足终止准则，最后将运算结果作为问题最优解。

经过多年的发展，遗传算法理论逐渐成熟，已经被成功应用于优化设计、模糊逻辑控制、神经网络、专家系统等领域。

2.2 粒子群算法（PSO）

粒子群优化算法（Particle Swarm Optimization，PSO）是由Eberhart与Kennedy提出的一种新的模拟鸟类捕食行为的全局优化进化算法[9]。该算法首先初始化一群随机粒子，然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己：一个是粒子本身所找到的最优解；另一个是整个种群目前找到的最优解。

粒子群算法结构非常简单，参数少，只需简单的数学运算便可以实现，自出现以来受到了广泛的关注，在组合优化[10-11]、控制器参数调节[12]等领域得到了大量的应用。

2.3 基于遗传粒子群算法的飞行冲突解脱

PSO与GA有很多共同之处：它们都起源于人类对生物学的研究，属于仿生计算范畴；都使用适应度函数来评价系统，群体根据适应度值进行复制；两种算法都经过不断的搜索，找到最优解。它们又有所不同，遗传算法具有交叉和变异操作，具有广泛的空间搜索能力，在搜索过程中不容易陷入局部最优，但是算法复杂，搜索速度慢，没有种群的移动，缺乏记忆功能，不能参考历史信息。粒子群算法结构简单，仅仅根据自己的速度来决定搜索，没有GA明显的选择、交叉和变异操作，具有运行速度快，拥有记忆功能等特点。本文将遗传算法和粒子群算法相结合，提出一种遗传粒子群算法解决多机冲突解脱问题。该算法既保持了个体之间信息交流，避免陷入早熟收敛与局部最优，又提高了搜索效率与加快计算速度。该算法步骤描述如下：

图1 算法编码机制示意图

步骤1随机产生初始种群Pop。算法采用二进制编码机制，种群中的任意个体Xi的维度为Q,Q=N×K×2,N为飞机数目，K为每架飞机在冲突区内航向调整的次数。编码机制如图1所示。

步骤2设定参数，确定遗传交叉概率pc,变异概率pm,粒子群惯性因子w,加速度系数c1、c2和最大迭代次数NCmax。

步骤3计算每个个体的适应度函数值，采用轮盘赌选择方法挑选出染色体对，以确定的概率进行交叉和变异操作，得到种群Pop′。

步骤4对Pop′中的个体进行适应度评估，得到个体最优位置pim和全局最优位置pgm,并按照式（5）和式（6）分别对种群速度和位置进行更新，产生下一代种群Pop。

步骤5判断是否已经达到最大迭代次数，如果到达，结束进程，输出结果；否则转至步骤3。

该算法的流程图如图2所示。

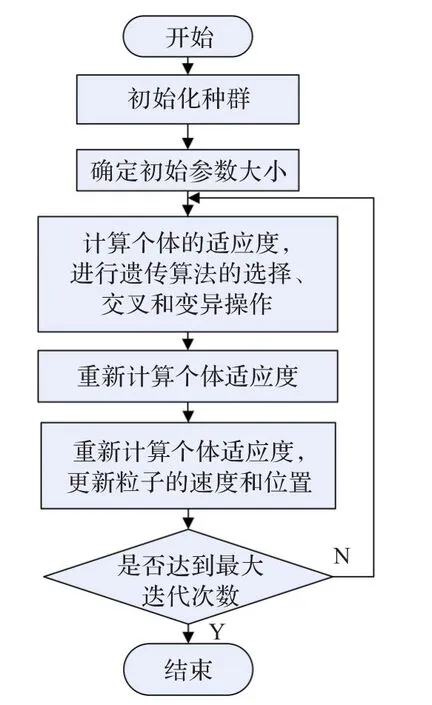
图2 遗传粒子群算法流程图

图3 （a）实例1的冲突解脱路径图

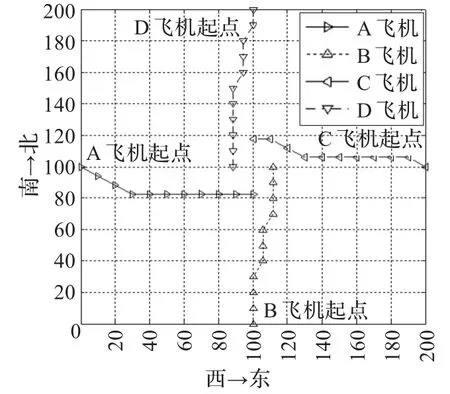
图3 （b）1到10步的冲突解脱路径图

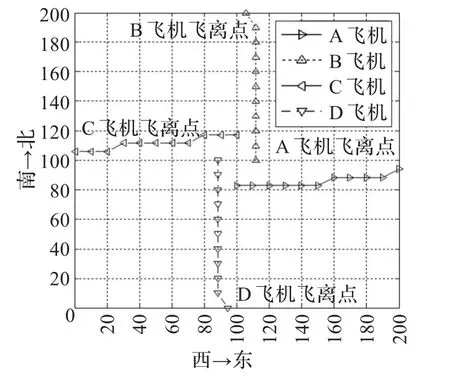
图3 （c）11到20步的冲突解脱路径图

3 仿真及验证

在仿真实验中，4架飞机以相同的速度飞行，把飞机的飞行时间分为20步，如不进行航线调整，在第10步时4架飞机将同时发生冲突。算法中，群体大小设480，对应着480条随机航路。交叉运算的概率设置为0.7，变异概率为0.01。粒子群的惯性因子w=0.8，加速度系数c1=c2=0.7。

实例1 4架飞机直线交叉通过冲突区，其中A飞机从西向东飞行，B飞机从南向北飞行，C飞机从东向西飞行，D飞机从南向北飞行。

经10次抽样记录，此算法平均在运行10次迭代后能收敛于理想的结果，平均耗时为2.31 s。图3（a）为实例1的冲突解脱路径，图 3（b）和3（c）分别为1到10步和 11到20步的解脱路径。图4为算法适应度函数值曲线。

图4 实例1的适应度函数值曲线图

为了评价本文算法的性能，将该算法所得到结果与文献[6]中的算法，以及二进制粒子群算法的规划结果进行了比较。表1列出了三种算法运行结果对比。

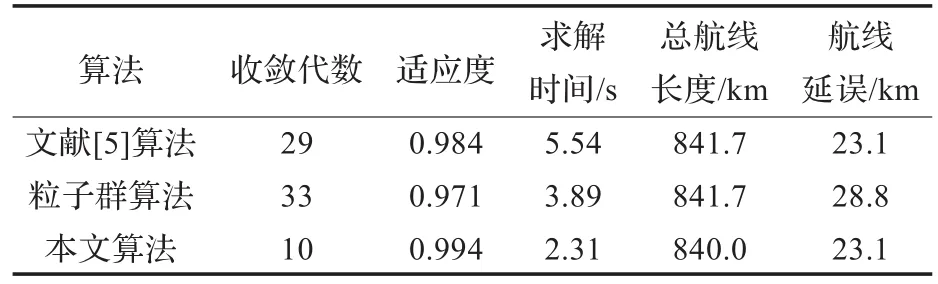
表1 实例1三种算法结果对比

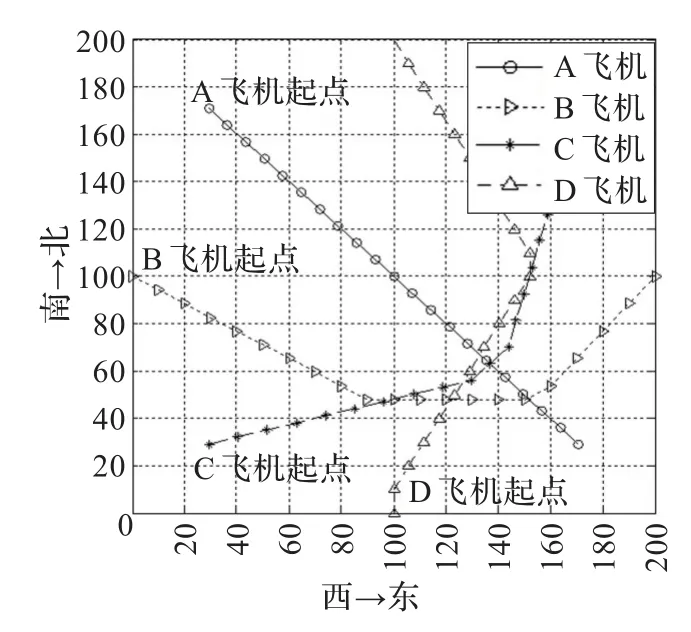
图5 （a）实例2的冲突解脱路径图

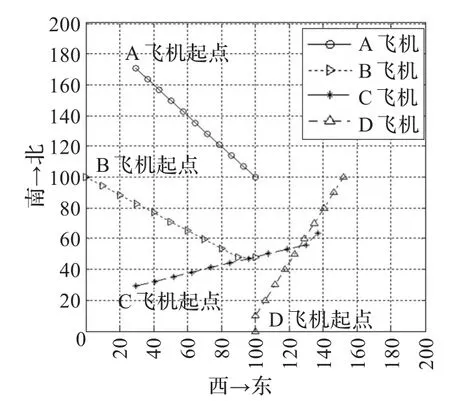
图5 （b）1到10步的冲突解脱路径图

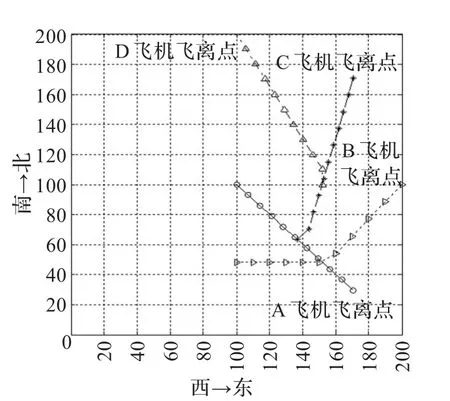
图5 （c）11到20步的冲突解脱路径图

实例2 4架飞机以45°交叉飞过冲突区，每架飞机的起始位置到冲突区的中心的距离为100 km，其中A飞机从西北向东南方向飞行，B飞机从西向东飞行，C飞机从西南向东北飞行，D飞机从南向北飞行。

经10次抽样记录，此算法平均在运行29次迭代后能收敛于理想的结果，平均耗时为7.12 s。图5（a）为实例2的冲突解脱路径，图5（b）和5（c）分别为 1到10步和11到20步的解脱路径。飞机间的安全飞行间距为20 km，图5中的4架飞机经过20步航向调整后，任意两架之间的间距都大于安全间距。图6为算法适应度函数值曲线。

表2为实例2中，本文算法与文献[1]中的遗传算法、文献[6]中的自适应遗传算法的规划结果对比。

表2 实例2三种算法运行结果对比

仿真实验证明，本文算法能够快速有效地解决同一冲突区内4架飞机的冲突解脱。由表1、表2对比结果可以看出，遗传粒子群算法在收敛代数和计算速度都优于其他两种方法，且收敛时的适应度值更高，规划出的路线更接近原航线，这就减少了飞机的燃油消耗和管制员的工作负荷。实验证明，遗传粒子群算法解决同一冲突区内4架飞机的飞行冲突问题效果更好。

4 结论

本文采用遗传粒子群算法有效地解决了4架飞机的飞行冲突。该算法综合了遗传算法的全局搜索能力与粒子群算法记忆功能和快速收敛的特点，计算速度快，搜索效率高，可以在相当短的时间内规划出飞行解脱航迹，且解脱后的飞机航迹平滑，更接近于原航线。本文假设飞机在固定高度层飞行，将飞行的运动限制在二维平面中，对于三维空间中的冲突解脱问题的研究，将是下一步的工作重点。

[1]Alliot J M，Gruber H，Joly G.Genetic algorithms for solving air traffic control conflicts[C]//Proceedings of the 9th Conference on Artificial Intelligence for Applications，Orlando，FL，USA，1993：338-344.

[2]Burdun I Y.An AI situational pilot model for real-time applications[C]//Proceedings of the 20th Congress on the International Council of the Aeronautical Sciences，Sorrento，Napoli，Italy，September 8-13，1996：210-237.

[3]Ghosh R，Tomlin C.Maneuver design for multiple aircraft conflict resolution[C]//Proceedings of the American Control Conference，Chicago，Illinois，2000，9：672-676.

[4]靳学梅，韩松臣，孙樊荣.自由飞行中冲突解脱的线性规划法[J].交通运输工程学报，2003，3（2）：75-79.

[5]裴志刚，李华星，王庆胜.模拟退火遗传算法在飞行冲突解脱中的应用[J].交通与计算机，2005，23（1）：115-117.

[6]赵源.航路飞行辅助决策仿真系统关键问题研究[D].西安：西北工业大学，2005：33-37.

[7]中国民航局.CCAR-91-R2一般运行和飞行规则[S].2007-11-22.

[8]Holland J H.Adaption in nature and artificial system[M].Ann Arbor：The University of Michigan Press，1975.

[9]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conferenceon Neural Networks，Perth，Australia，1995.

[10]陈自郁，何中市，何静媛.一种求解集合组合问题的离散粒子群优化模型[J].华南理工大学学报：自然科学版，2010，38（4）：141-145.

[11]魏静黄，王宇平.求解约束优化问题的改进粒子群算法[J].系统工程与电子技术，2008，30（4）：739-742.

[12]Kim T H，Maruta I，Sugie T.Robust PID controller tuning based on the constrained particle swarm optimization[J].Automatica，2008，44（4）：1104-1110.