智能虚拟布局设计关键技术研究与运用

宗立成，余隋怀，胡志刚

西北工业大学 机电学院 工业设计研究所，西安 710072

虚拟设计（Virtual Design）是20世纪90年代发展起来的研究领域，是基于虚拟现实技术的CAD设计方法。虚拟设计利用虚拟环境中丰富的交互式手段对计算机模型进行修改和实时数据反馈。虚拟布局设计中，建立布局对象与布局空间虚拟模型，借助直观的虚拟现实交互工具，设计师可以沉浸在虚拟布局环境中实时与虚拟场景交互，直接将待布物虚拟模型布置在虚拟空间中，布局设计将呈现动态感知。传统布局设计需要经过计算，才能获得布局方案，不具有交互性和动态修改性，虚拟布局通过虚拟现实技术可以实时看到布局立体效果，通过及时反馈和修改参数，实现布局优化设计的可视化。加拿大Alberta大学Liang与green[1]开发的JDCAD系统通过三维操作进行几何造型设计研究，在三维形状草图绘制方面获得一定成果。NASA（美国国家航空宇航局）最早借助虚拟设计技术对航空器进行布局、设计以及分析[2]。Smith等[3]采用三维交互式虚拟设计对制造业设备布局提出布局方案。Korves和Iqbal[4]分别利用虚拟设计技术求解工厂布局问题。周前祥[5]以虚拟布局场景实现实验参数设置，针对航天器座舱提出布局工效学实验系统。查建中教授[6]在虚拟环境下建立了布局模型机器人机交互接口，实现了三维布局问题求解的人机结合性。王少梅[7]使用MultiGenCreater软件，建立码头场景中三维模型的数据并开发了码头布局软件，实现码头动态布局设计。利用虚拟设计技术进行布局问题的研究是布局问题求解的方向之一。

1 智能化布局问题建模

计算智能技术的发展将极大促进布局问题的研究。现代学术研究已经证明布局问题具有NP难度，在有限的时间内很难获得最优解，启发式算法的出现和发展就证明了这点。启发式算法利用专家经验和知识，建立规则集指导计算机在解的空间域搜索满意解，而并非最优解。目前，鉴于布局问题的复杂性、约束性和建模困难等特点，智能计算技术被广泛采用。其中包括遗传算法、模拟退火算法、小生境技术、序列三元组编码等。

模拟退火算法具有一定的概率落入局部最优的陷阱中，但经过足够长的时间也可以收敛到全局最优解。任何算法都有其缺陷和不足，为了避免模拟退火算法的局部最优陷阱，引入人机交互模块，通过虚拟环境，实时的人机交互技术可以指导算法优化方向，避免落入局部最优。其质量和效率受三方面因素的影响。（1）初始温度。初始温度的选择在一定程度上会使布局方案落入局部最优陷阱中或增加计算时间无法忍受。（2）温度下降系数。在实际的物质退火状态中，降温过程是缓慢进行的，在算法中也同理，每步降温值太小会造成计算时间过长，每步降温值过大，则不能获得较好的解。（3）循环次数。循环的目的是为了改善目标函数值，因此，在允许的时间内应尽量增大算法的循环次数，以保证获得最优解。

2 基于智能虚拟技术的规则物体布局设计关键技术

布局问题的研究具有广泛的工程应用背景。自1831年Gauss（高斯）对Lattice（格）装填问题的研究开始，经过几代人的努力，目前对布局问题的研究初见成效。纵观现有文献资料，布局问题可以分为一维、二维、三维布局问题。根据研究内容，布局问题又可细分为切段问题和装填问题，其中装填问题按照研究理论体系分为规则图形装填和不规则图形装填，本文所研究的就是规则图形装填布局问题。

2.1 虚拟设计建模

布局问题的研究发展到目前为止，已经不单单局限于数学角度和数学模型求解，传统的单独采用计算机求解布局优化问题往往很难以获得优化解。随着虚拟现实技术的发展，特别是虚拟设计技术的发展，可以将专家领域的知识、经验引入到智能虚拟布局设计问题中，使专家、设计师从繁琐的计算和操作工作中解脱出来，系统地融入到虚拟设计进程中，充分发挥专家的知识、经验和关键决策作用。

虚拟现实技术为虚拟设计研究提供保障，虚拟现实具有交互性、沉浸感和想象性，设计师在虚拟环境中是主动参与者，通过虚拟现实技术将复杂、抽象的计算机模型数据空间直观地表现出来。设计师通过数据手套等输入设备在虚拟环境中操作待布设备，每步操作后经过计算机系统处理，设计师可以通过三维头盔或数字眼镜等输出设备看到虚拟环境中设备的布局结果，这种显示状态是实时反馈的。虚拟布局设计将设计师实时融入布局设计和优化进程中，设计师在三维状态下，可以自由地观察、操作、干涉、修改布局状态，这种人机交互式的布局方法可以更快地获得最优设计方案，避免算法的缺陷，最终获得优化布局方案。

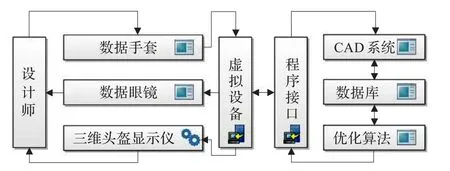
图1 虚拟设计系统架构

基于专家系统的虚拟布局设计方法求解复杂布局问题，将成为复杂布局问题自动化求解的发展方向。

2.2 规则图形布局问题及其编码

2.2.1 规则图形布局问题

规则图形装填问题是布局领域研究较多的方面，在实际工程中，绝大多数不规则物体的布局问题都可以转化为规则图形进行布局优化设计，这也是解决复杂不规则产品布局问题的有效方法。

Beasley[8]利用数学规划法对矩形装填问题进行求解，但由于受限于算法只可解中等规模的装填问题。Younis[9]提出了一种0-1混合集成规划公式，对若干不同矩形进行布局。Tam[10]等通过启发式算法，利用专家或设计师知识和经验来解决矩形布局问题。随着计算机信息技术的发展，近年来计算智能技术也被大量应用于矩形布局问题中。Georgis[11]等提出了自适应搜索算法的模拟退火法，在允许的时间内，对布局问题进行求解。黄文奇等[12]通过拟物和拟人思路，给出了圆形装填问题的启发式算法。陆一平等[13]提出膨胀装填布局的策略，通过施加膨胀-排斥操作，实现自动产生布局位置，具有较强的直观性和集聚性。

本文讨论的是规则矩形块布局优化问题，多种矩形块物品装填问题的定义为：给定一个约束宽度为W，长为L，高位H的装填空间K和N种不同类的待布物品A1，A2，A3，…，An，第i(i=1,2,…,n)种物品有 Mi个，第i种待布物的尺寸为ti×ri×pi。求解待布物在K空间中的最优装填方案，使其在满足约束条件的情况下空间占用率最高，用在机械产品布局问题上，就是产品组合优化在满足约束条件的情况下，占用空间最小，即消耗材料最小、造价最低、运输最方便等。

规则图形装填问题的研究在机械产品、大规模集成电路、建筑物布局、工厂场地布局、工装平台等方面具有广泛的工程应用背景。

2.2.2 序列三元组编码

陆一平在《三维矩形块布局的序列三元组编码方法》一文中，已经证明序列三元组编码方法在求解三维矩形装填问题的P-Admissible的，因此本文不再对此进行论述。

序列三元组编码方法在求解矩形块布局问题是，其组合数为(n!)3，即是4个待布物体，组合数也达到13 824次。当布局物体规模增大时，组合爆炸不可避免。因此，结合模拟退火算法，对布局问题进行数学建模。

本文采用模拟退火思路进行编码，具体描述如下：将待布物编号为1,2,…,n；将待布物编号的一个次序排列即为序列Γ=k1,k2,…,kn，使用三个相互独立的序列组成三元组(Γ1,Γ2,Γ3)来表述装填优化的解空间。

为了更好地理解三元组的编码思路和方便后期算法求解，进行如下定义：

定义1使用二值矩阵Z表示序列Γ：

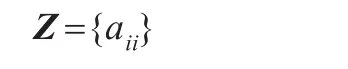
式中，Z为n×n的二值矩阵，即aii只能取0或1；如果在序列 Γ中，编号 j在i之后，则aij=1，否则aij=0，并规定在序列Γ中，所有对角线元素都为0。

定义2在n×n的二值矩阵中，会出现以下情况：

Pij的取值为 0或 1；对角线元素 Pii=0 ；Pij⋅Pji=0 ；Pik=1且 Pkj=1，则一定有 Pij=1。

定义3在n×n的二值矩阵中，如果所有元素都为1，那么为满矩阵，记为F；如果对角线元素为1，而其余元素为0，那么为单位矩阵，记为I。

定义4如果三个部分序列P1，P2，P3，P1+P2+P3+(P1+P2+P3)′=F-I ，则称P1，P2，P3是正交的。

定义5如果三个部分序列P1，P2，P3使得P1+P2+P3是序列，则称P1，P2，P3是序列的三元分解。

定理1如果A1，A2，A3是序列矩阵，则如下矩阵G1，G2，G3是序列的三元分解：

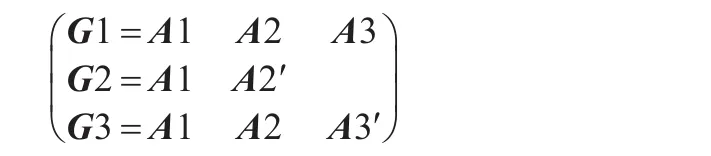
定理2如果G1，G2，G3是序列的三元组，且G1+G2，G2+G3，G3+G1是部分序列，则必有三个序列A1，A2，A3，通过定理1的计算得出G1，G2，G3。

采用三元组(Γ1,Γ2,Γ3)对优化布局问题进行编码，译码过程如下：

将三元组 (Γ1,Γ2,Γ3)表述成序列矩阵（A1，A2，A3），按照定理1求解出序列三元解G1，G2，G3，使其产生G1，G2，G3约束下的装填空间所占用的三度长度L1，L2，L3，优化目标函数即装填空间的体积，V=L1×L2×L3。

在三元组序列中，任何一个装填布局都可以适用序列三元分解为G1，G2，G3表达，而且，任何一个序列的三元分解可以通过序列三元组(Γ1,Γ2,Γ3)获得，通过上述方法译码的三元组编码所构成的解空间中一定包含了装填块布局的优化解。

代码反求译码过程如下：

计算人工移动后视图的序列三元分解G1，G2，G3。由定理2，可以得到布局方案的三个序列矩阵A1，A2，A3。

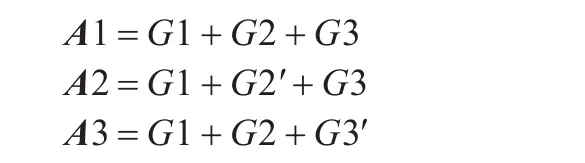
由序列矩阵A1，A2，A3，逆向求解当前模型对应的序列三元组 (Γ1,Γ2,Γ3)。

2.3 模拟退火算法策略

模拟退火算法具有良好的寻优性和跳出局部最优陷阱能力，其中初始温度、温度下降系数和循环次数的设定会影响算法的质量效率。在本文中，模拟退火算法的优化目标函数表述如下：

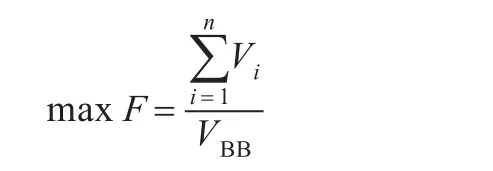
式中，n为待布物体的数量，Vi是第i个待布物体的体积，VBB为布局后包围盒的体积，VBB=l×b×h。

接受概率函数表述如下：

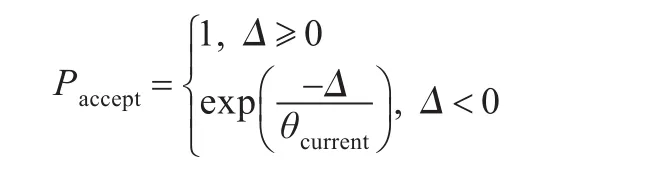
式中，Δ=Fnew-Fcurrent，Fnew为新状态下的目标函数值，Fcurrent为当前状态下的目标函数值。

3 智能虚拟布局设计系统构建

基于虚拟现实的虚拟布局设计方法，提出了虚拟环境下利用三元组编码和模拟退火算法求解规则布局问题。设计师通过虚拟设备进入虚拟环境中，实现传统布局设计算法所不具备的实时反馈和观察算法进程及布局算法的搜索方向，同时借助数据手套对待布物或待布容器进行操作，经过算法代码反求，获得当前状态下布局状态编码，进行优化计算。如此循环进化获得目标函数值最优，最终布局方案最优。智能虚拟布局与传统布局方法不同在于优化计算过程的人机结合性，传统算法只能在获取计算方案之后，进行评价，智能虚拟布局方法直接将专家知识、经验以及评价融入在优化设计进程中，最终获得方案具有最优性。算法流程如图2。

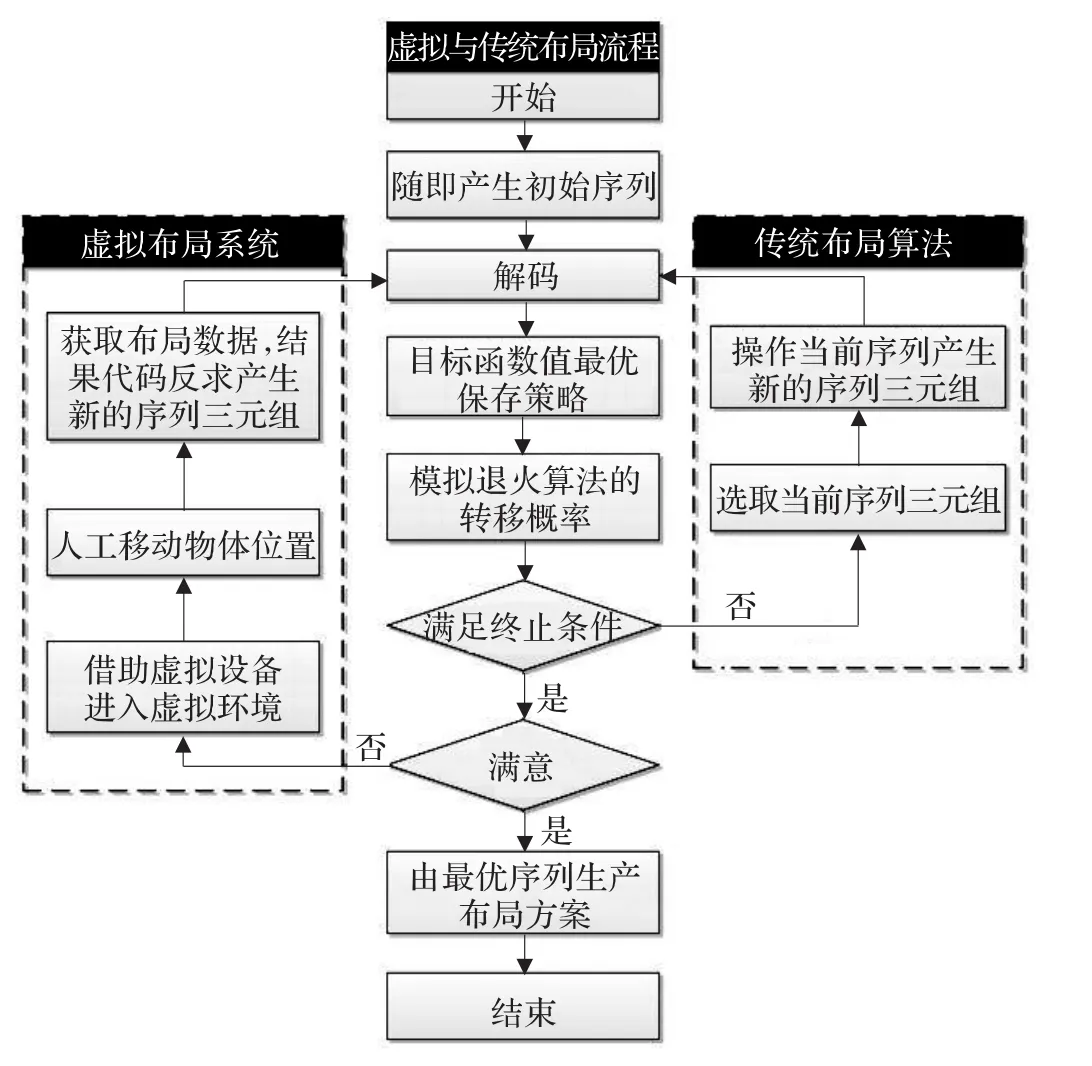
图2 虚拟与传统布局设计流程图

4 布局实例

以某型号整合机柜为例，待布设备n为4，终止条件为达到最大循环次数（本例取100）或空间利用率大于0.90。

初始温度设定T0=10 000，线性降温系数DT=1.0，初始序列三元组随即产生，进行求解，详细待布设备参数见表1和表2，表3为详细布局结果参数。

表1 待布设备参数

由于待布设备不是规则图形，为了计算方便，对待布设备进行规则转化。待布设备最终需要互不干涉的布置与机柜内部，因此，进行矩形转化并不会影响布局方案计算，反而会加快计算进程。详细参数见表2。

经过计算求解，获得近似优化解和中间解，如图3所示。根据求解获得的最优布局方案，将各待布设备进行布置安放，进入详细设计阶段，经详细设计阶段，最终获得机柜产品最终效果图，如图4所示。

5 结束语

智能虚拟布局设计为布局设计提供了新的发展方向和研究方法，使得设计师可以将自身知识和长期积累的经验系统地融入布局优化进程中，根据实时交互和反馈控制优化设计方向，最终获得的解具有最优性。智能虚拟设计方法有效地避免传统的数学计算方法在求解布局问题时的局限性，借助虚拟现实技术，实现布局优化设计的虚拟三维显示。本文在采用序列三元组编码和模拟退火算法策略的基础上，对布局问题进行智能虚拟设计，根据布局实例显示，本方法具有很好的发展前景，实时的人机交互也为布局方案评价奠定基础。在实际工程中，规则图形布局比较常见，不规则布局也可以借助一定的方法转化为规则布局问题进行建模求解，但有些特殊复杂产品布局，会受性能约束限制，转化为规则图形会影响其布局方案最优性，因此，建议在本文的基础上对不规则复杂产品布局设计问题进行继续研究。

表2 待布设备详细信息

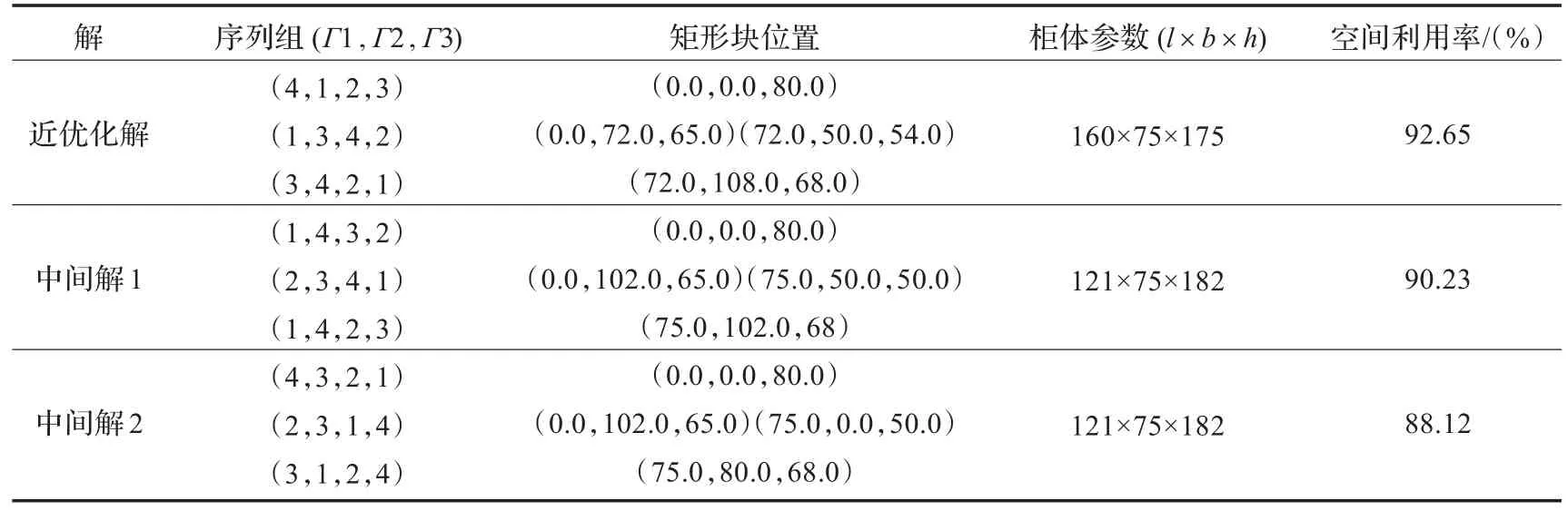
表3 布局结果详细参数

图3 布局结果

图4 最终布局方案效果

[1]Liang J，Green M.JDCAD：a highly interactive 3D modeling system[J].Computers&Graphic，1994，18（4）：499-506.

[2]Bryson S，Levit C.The virtual wind tunnel[J].IEEE CG&A，1992，12（4）.

[3]Smith R P，Heim J A.Virtual facility layout design：the value of an interactive three-dimensional representation[J].International Journal of Production Research，1999，37（17）：3941-3957.

[4]Lqbal M，Hashmi M S J.Design and analysis of a virtual factory layout[J].Journal of Materials Processing Technology，2001，118（1）：403-410.

[5]周前祥，陈善广，姜国华，等.航天器座舱布局功效学仿真实验系统—虚拟座舱的研究[J].系统仿真学报，2001，13（3）：291-293.

[6]唐晓君，查建中，陆一平.基于虚拟现实的人机结合方法及其在布局中的应用[J].机械工程学报，2003，39（8）：95-100.

[7]张煜，王少梅.虚拟现实技术在码头布局设计中的应用[J].计算机工程与设计，2006，27（23）：421-423.

[8]Beasley J E.An exact two-dimensional non-guillotine cutting tree search procedure[J].Operational Research，1985，33：49-64.

[9]Younis N A，Cavalier T M.On locating part bins in a constrained layout area for an automated assembly process[J].Computers&Industrial Engineering，1990，18（2）：111-118.

[10]Tam Y，Wu Yuliang，Huang Wenqi，et al.Effective quasi-human based heuristic for solving rectangle packing problem[C]//IEEE Asia-Pacific Conference on Circuits and Systems-Proceedings，1998：137-140.

[11]Georgis N，Petrou M，Kittler J.On the constrained rectangle packing problem[J].International Journal of Modeling and Simulation，2000，20（4）：293-299.

[12]黄文奇，许如初.支持求解圆形packing问题的两个拟人策略[J].中国科学：E辑，1999，29（4）：347-353.

[13]陆一平，查建中.求解装填布局问题的膨胀算法[J].计算机学报，2001，24（10）：1077-1084.